基于虚拟节点的BP无线传感器网络定位算法

孙 凯，刘润杰，申金媛

(郑州大学信息工程学院，河南郑州450001)

0 引言

无线传感器网络节点的位置是网络中必要的基础信息，节点的准确定位是无线传感器网络关键问题之一。目前，根据网络中是否需要测量节点之间的真实距离，定位算法可分为基于测距的方法(range-based)和距离无关的方法(range-free)［1］。前者测量利用节点之间的距离或者角度信息实现节点自身定位，典型的算法有TDoA，RSSI，ToA，AoA等。基于测距的定位方法需要额外硬件的支持，并且会产生大量计算和通信开销;距离无关的定位方法仅依靠网络的连通度等信息实现节点自身定位，无需额外的硬件，但是定位精度却不如前者，因此，如何提高距离无关定位方法的定位精度得到了学者们广泛的研究。

在Range-Free方法中，比较典型的2种算法是由 Bulusu N提出的Centroid algorithm［2］和由Nicelescu D利用矢量路由和GPS定位原理提出的 DV-Hop［3］算法。而在国内，李兆斌等人也提出增强的质心定位算法(ACLA)［4］;于宁等人基于限制跳数思想提出LDV-Hop算法［5］。

现有定位算法都表明锚节点的比例越高，定位的精度越高［6，7］，但锚节点比例的增加会增加无线传感器网络的成本。本文首先将BP神经网络用于无线传感器网络的节点定位，为了进一步提高节点的定位精度，提出了基于次锚节点的BP定位估计方法。次锚节点的引入相当于虚拟地增加了锚节点的比例，这样就减少了应用成本。

仿真结果表明:BP神经网络具有较小的定位误差，并且，次锚节点的引入也可进一步提高定位精度。

1 基于BP的定位算法

1.1 BP 结构模型

本文首先采用两层BP神经网络对未知节点进行定位。为了简化定位估算系统的结构和成本，采用距离无关的集中式定位算法。采用节点间的最小跳数信息，并发送给网络中的中心节点(如一台服务器)，由它运行定位算法，这样可以保证运行算法的计算量和存储量以及能耗。其中，节点间的最小跳数通过以下方法确定:锚节点向邻居节点广播自身位置信息的分组，其中包括跳数(初始化为0)和自身ID信息。接收节点记录到锚节点的跳数。若收到来自同一锚节点的分组，且其中的跳数比原来收到的要大，则忽略该分组。然后将跳数加1，继续向邻居节点广播该分组，这样网络中的节点能够记录下到每个锚节点的最小跳数。

假设共有N个随机部署的节点，用n=1，2，…，N来表示，其中前M个为锚节点，其余为未知节点。Bi=(xi，yi)表示第i个节点的位置。令Si=［si1，si2，…sim…siM］表示各锚节点之间的最小跳数，其中，sim表示第i个锚节点到第m个锚节点的最小跳数，i=1，…，M，m=1，…，M，当 i=m时，sim=0。令 Sj=［sj1，sj2，…sjm…sjM］表示各未知节点到锚节点的最小跳数，其中sjm表示第j个未知节点到第m个锚节点的最小跳数，j=(M+1，M+2…N)，m=1…M。输入层神经元的个数M由锚节点数目决定，隐含层神经元个数通过经验选取，输出层的2个神经元的对应于节点位置的坐标(x，y)。

1.2 利用BP估算位置

基于BP的定位算法分为训练和估计2个阶段。在训练阶段，首先利用锚节点对网络进行训练，训练的样本选择网络中所有的锚节点，训练的输入是锚节点之间的最小跳数，即 Si=［si1，si2，…sim…siM］，训练的输出是对应锚节点的位置 Bi=(xi，yi)，i=1…M，m=1…M。估计阶段的输入是每个未知节点到各锚节点之间的跳数，即Sj=［sj1，sj2，…sjm…sjM］，输出是对应的未知节点的位置，Bj=(xj，yj)，j=(M+1，M+2…N)，m=1…M。

2 基于虚拟节点的定位算法

2.1 次锚节点

研究表明:锚节点比例的增加可有效地提高未知节点的定位精度，但是增加锚节点比例同时也将增加无线传感器网络的应用成本。为了节约成本并有效提高网络的定位精度，本文提出了次锚节点的概念，将部分未知节点转化为锚节点，从而进一步对未知节点进行定位。

2.2 次锚节点的选择

引入次锚节点带来的一个困难是如何从未知节点中选取合适的次锚节点，理论上应该先对未知节点的位置进行估计，然后，选取定位比较准确的未知节点作为次锚节点，但是在实际中并不知道未知节点的位置，无法判断未知节点的估计位置和实际位置的误差。为了解决这个问题，引入了虚拟节点，并借助于虚拟节点在未知节点中选择定位精度较高的未知节点作为次锚节点。

2.2.1 虚拟节点

虚拟节点即在现实中并不存在的点，它们不具备节点间通信和信息转发的能力，但是可以假设在网络中存在着随机分布的这样的一些节点，并且它们的位置是假设为已知的。假设网络中有P个虚拟节点，位置是Ck=(xk，yk)，令Sk=［sk1，sk2，…skm…skM］表示虚拟节点到各锚节点的最小跳数，其中，skm表示第k个虚拟节点到第m个锚节点的最小跳数，k=1，2，…P，m=1…M。

2.2.2 跳数的转化

虚拟节点的定位首先需要它们到各锚节点的最小跳数，由于虚拟节点不具备节点间通信和信息转发的能力，因此，不能直接找虚拟节点和锚节点之间的最小跳数，为此可将虚拟节点和锚节点的距离转化为跳数。本文首先计算虚拟节点和锚节点的距离，然后，将此距离和节点的无线射程作比较。如图1，节点A为锚节点，节点B和C为虚拟节点，R是A的无线射程。虚拟节点C和锚节点A的距离DAC＜R，首先可以确定虚拟节点C和锚节点A之间是一跳;而虚拟节点B和锚节点A的距离DAB＞R，因此，它们之间的跳数大于一跳。在多跳的情况下，A和B的跳数不能直接根据它们的距离确定，而是综合考虑B和邻居节点的跳数信息而最终确定。

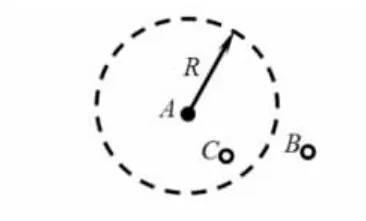
图1 跳数转化图Fig 1 Transformation diagram of Hop number

2.2.3 虚拟节点的选择

当知道了虚拟节点和锚节点的最小跳数后，可以用训练好的BP神经网络估计每个虚拟节点的位置，此时BP网络的输入是Sk=［sk1，sk2，…skm…skM］，网络的输出是对应虚拟节点的估计位置 C'k=(xk，yk)，k=1，2，…P，m=1…M。

由于虚拟节点的位置是假设为已知的，这时就可以将虚拟节点的估计位置和精确位置比较，即C'k和Ck，从中选出Q个误差小的虚拟节点，它们到各锚节点的最小跳数设为Sq=［sq1，sq2，…sqm…sqM］，q==1，2，…Q，m=1…M。为了进一步确定次锚节点，假设到所有锚节点的最小跳数都相同的节点的位置是接近的。基于这种思想，寻找Q个误差小的虚拟节点到各锚节点的最小跳数Sq=［sq1，sq2，…sqm…sqM］和具有到各锚节点的最小跳数 Sj=［sj1，sj2，…sjm…sjM］相同的未知节点，并将这些未知节点确定为次锚节点。

如图2所示，假设网络中有4个锚节点(节点1～4，实心圆)，9个未知节点(节点5-13，空心圆)，8个虚拟节点(节点14-21，三角)。假设经过锚节点和未知节点的信息转发以及虚拟节点将距离转换为跳数后，可以得到所有节点之间的跳数。用BP神经网络首先预测8个虚拟节点的估计位置，然后和它们的准确位置相比较。假设找出误差比较小的虚拟节点为16，17，19，21，然后寻找有没有和虚拟节点16，17，19，21到各锚节点(1～4)跳数相同的未知节点。假设未知节点8和13分别和虚拟节点17和21到各锚节点的跳数相同，最后，据此确定未知节点8和13为次锚节点。

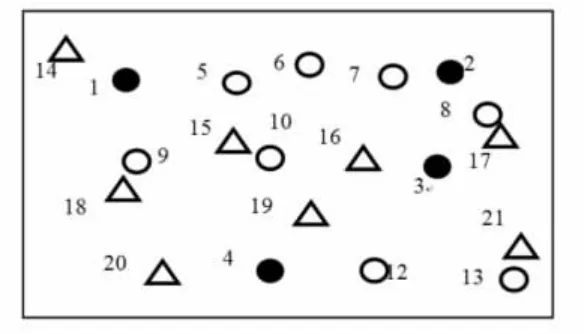
图2 寻找次锚节点图示Fig 2 Icon of searching for sub-anchor node

2.3 次锚节点的应用

找到次锚节点后，重新构建BP神经网络结构，将锚节点和次锚节点共同作为网络的锚节点，重新训练网络。新BP网络仍然采用两层网络结构，训练完毕后，对所有的未知节点重新定位。

3 仿真与分析

为了检验所提方法的性能，对质心(centroid)算法，DVHop算法，BP的定位算法，随机选择未知节点作为次锚节点的算法(RN-BP)以及利用虚拟节点选择次锚节点的方法(VN-BP)分别在Matlab的平台上进行了一系列仿真。仿真中所有节点都随机分布在100 m×100 m的区域内。由于BP神经网络的预测结果受到初始权重的影响，为了仿真结果能客观地反映所提方法的优劣性，每组不同条件均仿真运行100次，然后，取定位误差的平均值进行分析比较。

为更好地分析所提算法的性能，本文在3种不同的情况下仿真分析:1)无线射程不同的仿真;2)锚节点比例不同的仿真;3)总节点数不同的仿真。

3.1 定位误差和无线射程

对无线射程不同的情况进行仿真中共有200个节点，其中10个锚节点，各种算法定位误差与无线射程关系如图3所示。在相同的无线射程下，BP算法的定位误差比Centroid算法小;在无线射程小于40 m时，DV-Hop算法的定位误差比BP算法小，但是无线射程大于等于40 m时，DV-Hop算法的定位误差却比BP算法的高。引入次锚节点后，VN-BP算法的定位误差比BP算法降低了平均7.37%，这说明次锚节点在不同的无线射程下对降低定位误差是有效的;同时VN-BP的定位误差也比RN-BP高降低了7.42%，这说明在各种不同的无线射程下，虚拟节点的引入对降低定位误差均是有效的。

3.2 定位误差和锚节点比例

对锚节点比例不同的情况进行仿真中共有200个节点，无线射程设为40 m，结果如图4所示。仿真中5种算法的定位误差都随着锚节的比例增加呈下降趋势。在相同的条件下，BP算法的定位误差比DV-Hop算法和Centroid的误差降低了平均14.806%和10.35%，尤其是当锚节点比例大于15%时，BP算法的定位误差迅速下降。引入次锚节点后，VN-BP算法的定位精度又优于BP算法，定位误差降低了平均3.656%，这表明在不同的锚节点比例下次锚节点对降低定位误差的有效性;同时VN-BP的定位误差比RN-BP算法降低了平均2.346%，这也表明在不同的锚节点比例下虚拟节点的引入对降低定位误差均是有效的。

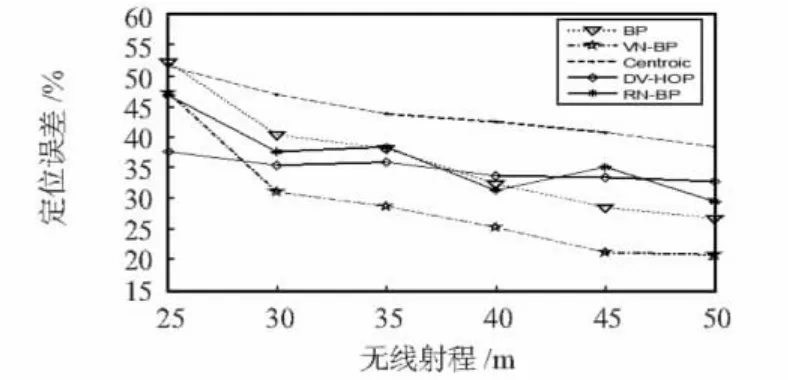
图3 无线射程和定位误差Fig 3 Wireless range and positioning error

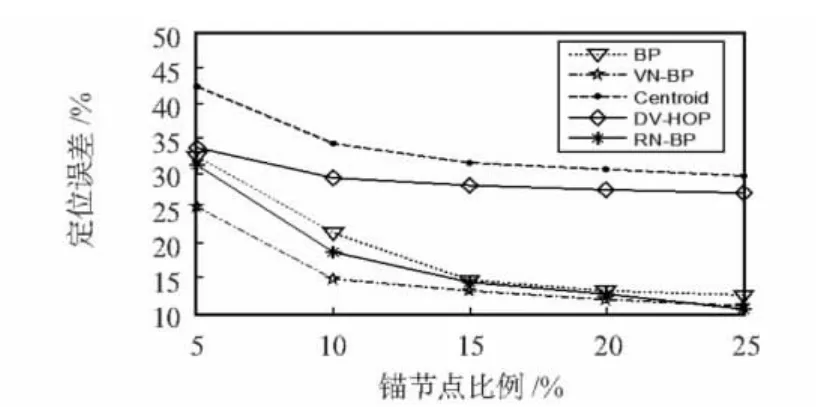
图4 锚节点比例和定位误差Fig 4 Anchor node proportion and positioning error

3.3 定位误差和节点数

对总节点数不同的情况进行仿真中的锚节点比例为10%，无线射程设为40 m，结果如图5所示。随着节点数目的增加，5种算法的定位误差大体上呈递减趋势。在相同的条件下，BP算法明显优于Centroid算法，定位误差降低了平均13.5%;在节点数为100时，BP算法的定位误差比DVHop算法大，但在当节点数目大于200后，定位误差迅速降低，并小于DV-Hop算法的误差。当引入次锚节点后，VN-BP算法的定位误差比BP降低了5.866%，这说明次锚节点在不同的节点数下对定位精度的提高是有效的;同时VN-BP的定位误差比RN-BP算法降低了4.036%，这说明虚拟节点的引入在不同的节点数下对定位精度的提高也是有效的。

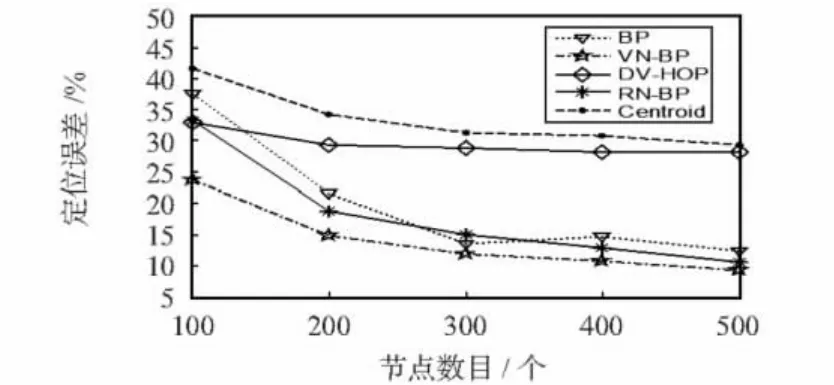
图5 节点数目和定位误差Fig 5 Number of nodes and positioning error

4 结论

针对网络中的锚节点比例因素，提出了应用次锚节点以提高锚节点比例，降低定位误差的算法。在定位误差的比较中，无论在无线射程，锚节点比例和总节点个数变化时，引入次锚节点算法的都要优于引进次锚节点前的算法和随机从未知节点里选取次锚节点的算法，这说明通过虚拟节点选取次锚节点对降低定位误差是有效的;其次，算法的定位误差总体上比Centroid算法和DV-Hop算法的定位误差小。因此，算法是一种适合无线传感器网络的定位算法。但并没有考虑虚拟节点的分布对算法的影响，因此，虚拟节点的分布有一定的研究价值。

［1］王福豹，史 龙，任丰原.无线传感器网络中的自身定位系统和算法［J］.软件学报，2005，16(5):857－868.

［2］Bulusu N，Heidemann J，Estrin D.GPS-less low cost outdoor localization for very small devices［J］.IEEE Personal Communications Magazine，2000，7(5):28－34.

［3］Nicolescu D，Nath B.DV-based positioning in Ad Hoc networks［J］.Telecommunication Systems，2003，22(1－4):267－280.

［4］李兆斌，魏占祯，徐凤麟.无线传感器网络增强的质心定位算法及性能分析［J］.传感技术学报，2009，22(4):563－566.

［5］于 宁，万江文，吴银峰.无线传感器网络定位算法研究［J］.传感技术学报，2007，20(1):187－192.

［6］Yin M，Shu J，Liu L.The influence of beacon on DV-Hop in wireless sensor networks［C］∥GCCW＇06 5th International Conference on Grid and Cooperative Computing Workshops，2006:459－462.

［7］刘少飞，赵清华，王华奎.基于平均跳距估计和位置修正的DV-Hop定位算法［J］.传感技术学报，2009，22(8):1154－1158.