RBF神经网络在断路器故障诊断中的应用*

2010-12-07郭凤仪马文龙

传感器与微系统 2010年9期

郭凤仪，马文龙，李斌

(辽宁工程技术大学电气与控制工程学院，辽宁葫芦岛125105)

0 引言

作为电力输配系统中应用最广泛的开关电器—高压断路器在电力系统中既要实现正常输电线路的投切，又要断开过载、短路等故障电流。由于断路器的基本功能体现在触头的分合动作上，因此，决定分合动作的操纵机构的工作性能对高压断路器的稳定性和可靠性起着极为重要的作用。

本文针对断路器分合操作模型具有很强的非线性以及受测试噪声的影响，通常对其进行在线故障诊断比较困难，而RBF神经网络能够以任意精度逼近任意复杂的非线性函数关系，可以实现那些难以用数学模型表示的复杂映像关系，能够自学习和自适应不确定系统的动态特性，具有较强的鲁棒性和容错性。因此，利用RBF神经网络的这些优点，将其运用到断路器的故障预测、故障诊断及模式识别当中，则可提高设备运行的安全性、可靠性、经济性及利用率。

1 RBF神经网络

RBF神经网络是利用RBF作为隐含层单元的基从而构成隐含层空间，这样，就可将输入矢量直接映射到隐，含层空间。当RBF的中心点确定以后，这种映射关系也就确定了。而隐含层空间到输出空间的映射是线性的，即网络的输出是隐含层单元输出的线性加权和，此处的权即为网络可调参数。由此可见，网络由输人到输出的映射是非线性的，而网络输出对可调参数而言却又是线性的。这样网络的权就可由线性方程组直接解出，从而大大加快学习速度并避免局部极小问题。

1.1 RBF函数网络模型

RBF神经网络由两层组成，如图1所示。输入层实现从x到Ψ(‖·‖)的非线性映射，输出层实现从Ψ(‖·‖)到y的线性映射。RBF函数网的输出层第j个神经元的输出可表示为

由于 Ψ(‖·‖)为高斯函数，因而，对任意 x均有Ψ(‖·‖)＞0，从而失去局部调整权值的优点。而当x远离c时，Ψ(‖·‖)已非常小，可作为0对待。因此实际上只当Ψ(‖·‖)大于某一数值(如0.06)时才对相应的权值w进行修改。经过这样处理后RBF神经网络也同样具备局部逼近网络学习收敛快的优点。

图1 RBF神经网络结构框图Fig 1 Structure diagram of RBF neural network

1.2 RBF神经网络训练步骤

RBF神经网络包含中心位置C和方差σ22个可调参数。此时，整个网络可调参数有3组，即各基函数的中心位置、方差和输出单元的权值。对于宽度参数有

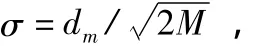
式中 dm为所选中心之间的最大距离;M为隐含层单元个数。

此时，一种较好确定C和W的方法为聚类方法实时调整中心并同时调整权值［3］。中心调整算法以聚类最小距离为指标，将输入数据集分类为K类，给出K个中心。权值更新算法是将输出层的每个节点或线性组合器是一个权值估计，可用最小二乘法求取。

以上过程实际是有指导学习，y是指导数据，通过对权值的训练后估计输出逼近实际输出。K均值聚类算法是独立的学习算法，与BP算法相比，由于参数调整是线性的，可获得较快的收敛速度，非常适合于系统的实时辨识与控制。

2 高压断路器分闸信号故障分析

本文以ZNY—6型高压真空断路器的分闸曲线为试验研究对象，通过现场试验获取线圈电流随时间变化波形如图2所示［4］。其固有分闸时间 To≤60 ms。t0－t1时，线圈通电，电流按指数规律上升。t1－t2时，铁芯开始运动，由于运动负荷增加，线圈电流显下降趋势。t2－t3时，铁芯运动停止，线圈电流又按照指数规律增至接近最大稳态值。t3－t4时，是上一阶段的延续，电流达最大稳态值。t4－t5时，辅助开关分断，迫使线圈电流迅速减小，直至最终降至为零值。

综上分析，由于此变化波形可直接反映断路器在分闸动作时操纵过程的动作状态，如，分闸速度、铁芯行程、稳态情况、开关关断等有无故障。因此，对电流波形进行检测就可实现线圈操纵状态的监测和断路器的故障预测。此外，对正常状态下分闸电流随时间变化的波形作多次测量，确认电流波形具有良好的重复性。

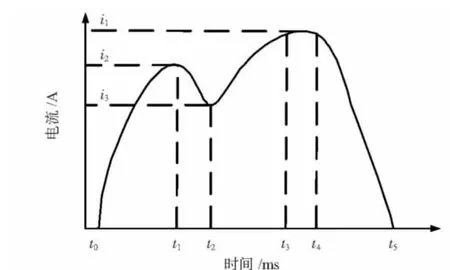
图2 分闸线圈电流随时间变化波形Fig 2 Waveform about the relationship between trip coil current and time

3 应用实例分析

利用RBF神经网络实现对高压断路器分闸线圈时间信号的监测过程进行建模。该模型易于实现且具有较高精度，可用于断路器操纵过程状况的预估。根据经验与试验结果分析，输入特征量要对输出影响大且彼此间不相关，选取为t1，t2，t3，t4，t5;输出特征量的选用则要代表实际可能出现的故障类型，选择操纵机构正常、分闸起始故障、铁芯行程故障、分闸稳态故障及开关断电故障等5类。

神经网络的输入输出特征量用编码表示且网络的输出值在0到1之间。数值大小表示对应的故障程度，0表示此种情况未发生，1表示此种情况发生，数值越接近1表示发生此类故障的几率越大;反之，则越小。针对本系统，设定输出值大于或等于0.65便认为有此类故障，小于0.65无此类故障。表1列出了高压断路器操纵机构的故障原因及其编码。