小波变换在风浪研究中的应用

赵利平，高 鹏

（长沙理工大学水利学院,长沙410076）

非线性、非平稳波浪理论在现代波浪学中占十分重要的地位，波浪的频谱估计是分析不规则波的能量分布和波浪变形的重要手段［1］。但以傅里叶变换为基础的传统谱估计方法将波浪过程视为平稳的随机过程，在风浪、波浪破碎等波形剧烈变化的研究领域存在着一定的局限性［2］，因为傅里叶变换在时域上没有分辨率，单纯的傅里叶变换不能同时在频率和时间上跟踪波浪过程在能量上的消涨，因此在傅里叶变换的基础上作出改进，提出了加窗傅里叶变换。但改进后的加窗傅里叶变换所加的函数窗尺寸固定，不能兼顾高、低频率时有较高的分辨率，所以又在此基础上提出了小波变换［3］。小波变换很好地解决了这一问题，并在通讯、图像处理等领域中得以广泛应用。

1 小波变换的基本原理

小波分析是1986年由Y.Meyer，S.Mallat及I.Daubechies等人的奠基工作而迅速发展起来的一门新兴学科，它是从傅里叶分析发展出来的。傅里叶变换是研究平稳信号的一种频域分析方法。但现实中风浪的波面变化通常是非稳定的，需要局部时间的频率分析，因此需要适合非平稳信号分析的小波分析［3］。

小波变换是将信号按不同尺度（频率）、不同位置（时间）分解的数学工具。不像傅里叶变换，仅与尺度有关，而与物理空间无关。虽然加窗傅里叶变换使之在物理空间上有了一定的分辨率，但一旦时间窗限定，由于测不准原理，无法兼顾高频和低频。而小波变换中的窗函数可以在低频时自动变宽，在高频时自动变窄，故小波变换能比傅里叶变换更好地“移近”观察，这是小波变换有别于前两者的地方，可以看做是自适应的加窗傅里叶变换，因此小波变换也有“数字显微镜”之称［4-6］。

信号能量如下

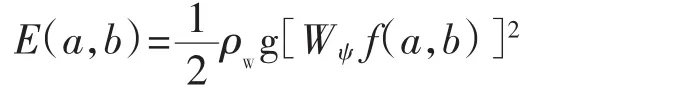
从而可以得到各个瞬时的能谱［7-10］。另外，利用小波的多分辨分析，可以将能谱中能量较为集中的频率的信号分解出来单独研究。信号分解见图1。图1中A为上一级信号中的低频部分，D为上一级信号中的高频部分，可以看到，每次分解得到的低频部分还会进一步分解，易得 F=D1+D2+D3+D4+D5+A5［7］。在进一步发展而来的小波包分解中，还会对每次分解得到的高频部分进行进一步分解，使分解的频带更加窄而多（图2）。

图1 小波分解示意图Fig.1 Wavelet decomposition

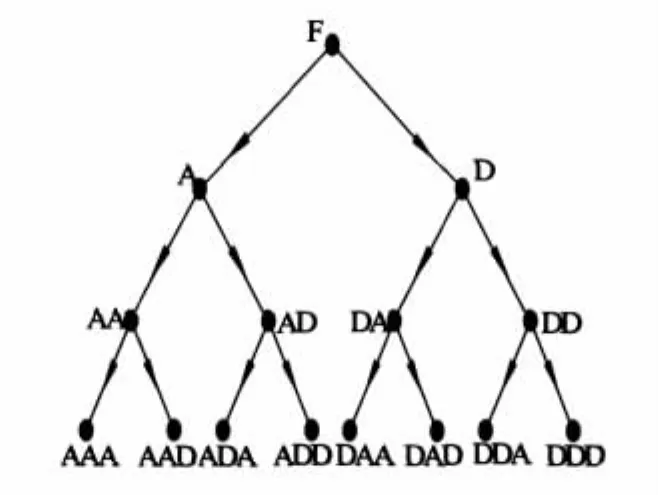
图2 小波包分解示意图Fig.2 Wavelet packet decomposition

2 现场观测

现场观测于2008年8月在岳阳市的南湖进行。数据采集使用交通运输部天津水运工程科学研究所生产的SG-2000系统，浪高仪1个（46#），压力传感器8个（50#～57#），50#～53#布置在0.3 m水深处，与入射波角度分别为 0°、90°、270°、180°，54#～57# 布置在水深为 0.5 m、0.7 m、1.0 m、1.4m 处且与入射波角度均为 0°。设定采样频率为10 Hz，采样数量分别为1 024、2 048和4 096，共采样240组。

观测地点前方水域宽阔，前方有2座山，测点正对风口，风向变化不大，测点后方12 m处有一片茂盛的芦苇，可以有效地消除波浪反射的影响，测点水位H=2 m，观测期间风速在2～5 m/s，观测时间12 d（图3）。在该测点设置8个压力传感器和一个浪高仪，浪高仪布置在桩柱离岸远的一侧，压力传感器布置见图4。

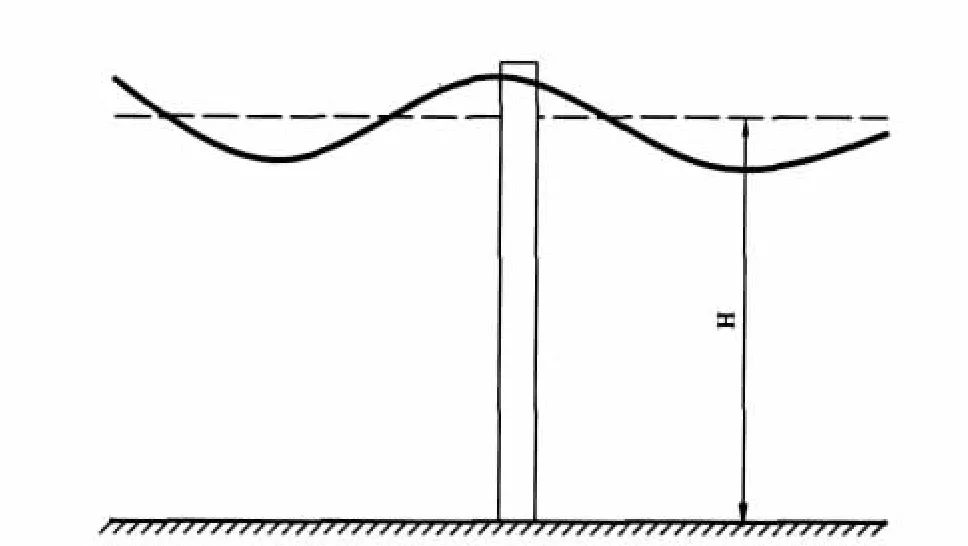
图3 观测示意图Fig.3 Observation sketch map

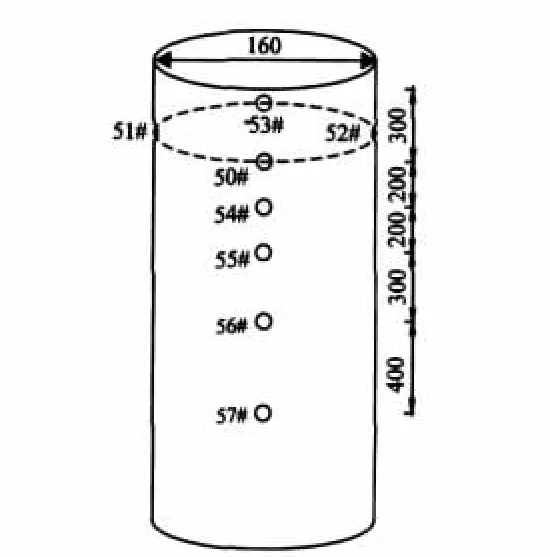
图4 压力传感器布置图（mm）Fig.4 Pressure sensor position

3 波浪信号的小波分析

3.1 波面信号分析

将测得的波面信号取均值，作为平均水位线，将原始数据减去平均水位线得到修正后的波面信号（图5）。

3.1.1 时频分析

本文选择在湍流研究中得到广泛应用的Morlet小波作为小波母函数，Morlet小波的选取主要基于以下优势：Morlet小波形状与通常风浪波面信号非常相似；不但能给出所分析信号的能量特征，还能给出相位特征。且就所分析的信号而言，不同的小波函数算出的小波系数的模差异很小［8-13］。

Morlet小波函数

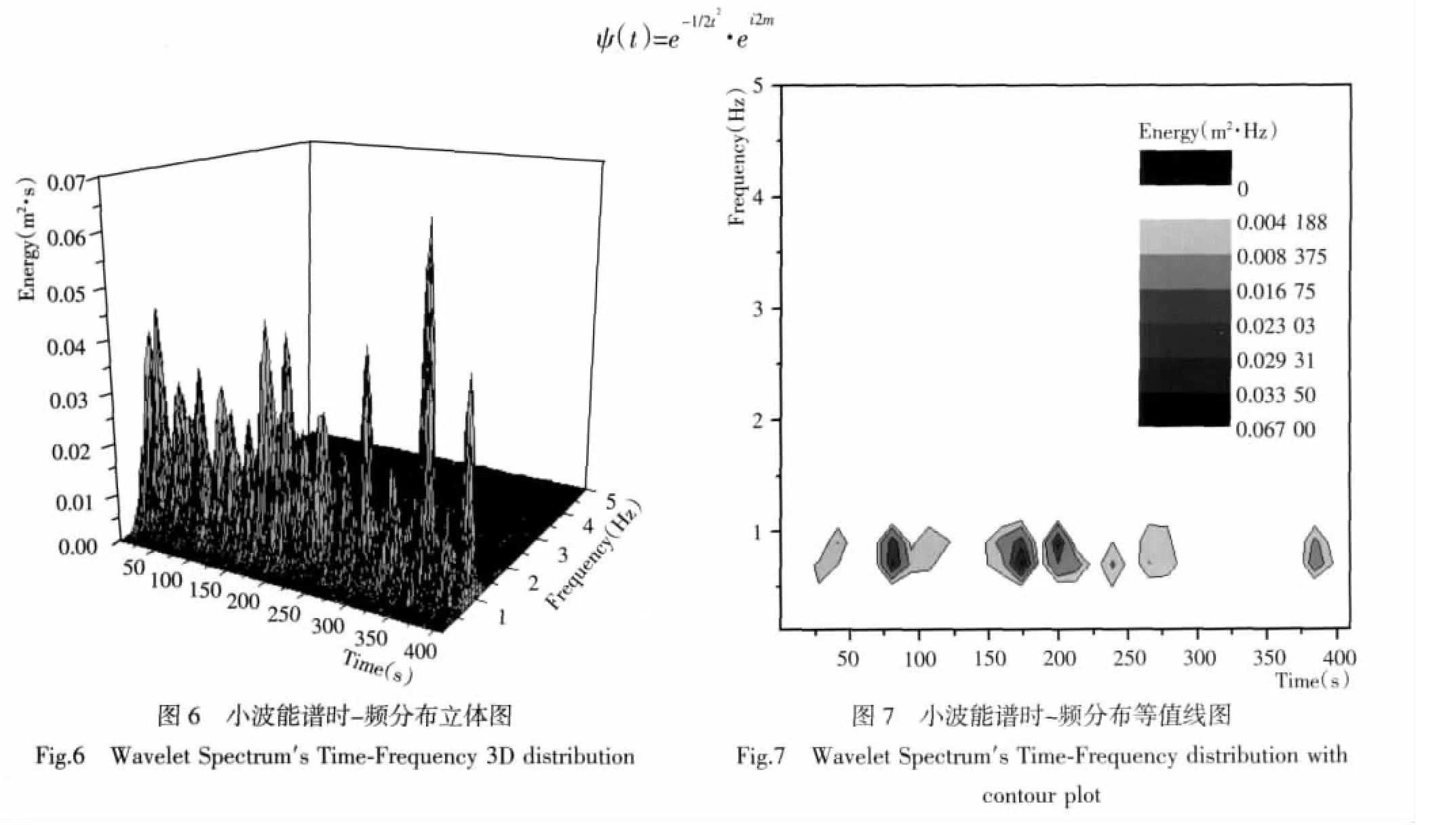
小波变换后所得小波变换系数平方后得到小波能量密度大小，从而建立能量与时间-频率的对应关系，如图6、图7。由图6和图7可以看出在时间轴上各个时刻的每一个能谱变化情况，在频率轴上每个瞬时的能量大小，即波面资料经过小波变换后，可以同时得到能量的时频分布。从图6可以看出，在固定频率下其时域上能量并非定值，而是有较大变化，但能量集中的频率是一致的。将小波能谱时频分布在时间轴方向上积分得到传统的能谱（图8）；对频率方向积分可以得到能量沿时间变化的关系（图9）。在图8中还将传统能谱与小波分析中得到的各个频率中的最大谱值对应的小波峰值能谱对比，从中可以发现小波峰值能谱比传统能谱普遍大10倍，其谱峰值相差约14倍，这是值得注意的。

3.1.2 小波分解

从图8可以看到波浪能量主要集中在0.25～1.25 Hz的频率间，可以通过4层小波分解得到各频率带的波的信号（图10）。其中S为原始波面，d1为2.5～5 Hz的波，可以看到d1的振幅基本都在0.01以下，在整个组成波中所占的能量很少；d2为1.25～2.5 Hz的波，它提供了一定比例的能量；d3为0.625～1.25 Hz的波，可以看到振幅与原始信号相似，提供了较大比例的能量；d4为0.312 5～0.625 Hz的波，可以看到所占能量较少；a4为0～0.321 5 Hz的波，振幅基本保持在0.005以下，提供的能量极少，这与图8是一致的。

3.2 波压力分析

将50#～57#测点测得的波压力数据取均值，作为零点压力值，并将原始数据减去零点压力值得到修正后的压力信号。应用Morlet小波作为小波函数进行计算，得到压力能谱（图11）。

图11中左边纵轴代表波压力的谱值，右边纵轴表示波面谱值。由图11可以看出，50#测点处的波压力谱峰对应的频率较波面谱大，谱峰宽度约为波面谱宽度的2倍；54#测点谱峰值较50#和波面谱要小1倍，谱峰频率与50#一致，且有不明显的次峰；55#测点谱峰值更小，谱峰频率较50#谱大，没有次峰；56#、57#测点没有明显的谱峰，能量几乎是均匀分布，从测得压力信号可以看到压力变化很小，几乎不受风浪影响。

由图12可以看出，3个测点的谱型几乎一致，只是与波浪方向垂直的测点所得到的谱型的主峰更高，能量更集中，51#测点的主峰最高而不与52#相等，这是因为实际观测时波浪的方向只是大体上正对50#测点，难免会有误差。

由于53#测点在观测支柱后方，受绕流影响很大，影响因素复杂，本实验测试频率较低，积累的数据不足，暂不讨论。

各测点的主峰、次峰频率及其对应的谱值见表1。

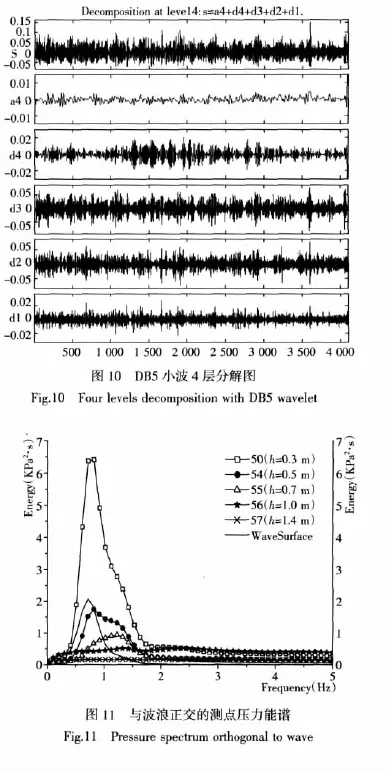
表1 各测点频谱分析表Tab.1 Frequency spectrum of survey points

4 结论

由于小波变换在时域和频域上都有良好的局部性，因此在波浪的非平稳过程、波浪的局部特性和非线性研究中具有重要的意义。

小波变换是加窗傅里叶变换的进一步发展，将小波能谱时频分布结果分别在时间和频率方向上积分，可以得到传统的能谱分析结果和传统的瞬时能量历程分析结果。

利用小波分解，可以对波浪进行多分辨分析，从而得到各个频带的波面信号，并针对所占能量组分最大的波作进一步分析。

通过时频分析，可以得到各个瞬时的波谱变化，从而可以了解波浪结构变化。

通过小波峰值能谱和传统能谱的对比，发现两者普遍相差1个数量级，最大相差约14倍，这是值得注意的现象，工程计算波浪要素时应该进一步注意各个瞬时的能谱。

利用小波理论对波压力进行分析得到压力能谱。其中正对波浪传播方向的压力能谱在0.3 m处的谱型与波面能谱相似，但水深达到0.5 m后则与波面能谱相差较大，而水深达到1 m后，能谱则比较平直，能量分布比较均匀了；而与波浪传播方向垂直的能谱谱型与正对波浪传播方向的谱型在0.3 m处几乎一致，只是谱峰略大。

本文数据是实地观测所得，受自然天气等非人为因素的影响，水深和波浪的方向均有一定误差。在数据整理中筛取了观测状态较好的用于分析计算，具有较高可信度。

本文对小波理论在波浪上的应用作了初步探讨，但还有很多问题没有解决，特别是压力能谱的研究还处于起步阶段，仍有待深入研究。

［1］文圣常，余宙文.海浪理论与计算原理［M］.北京：科学出版社，1984.

［2］李炎保，郄禄文，祝振宇.小波变换在随机海浪及相关课题中的应用与前景［J］.力学进展，2003，33（4）：541-547.LI Y B，XI L W，ZHU Z Y.Applications and Prospects of Wavelet Transform for Random Wave and Related Fields［J］.Advances in Mechanics，2003，33（4）：541-547.

［3］程正兴.小波分析与应用实例［M］.西安：西安交通大学出版社，2006.

［4］杨建国.小波分析及其工程应用［M］.北京：机械工业出版社，2005.

［5］周建萍，杨旭红，郑应平.基于小波分析的汽轮发电机组振动信号检测［J］.上海电力学院学报，2008，24（3）：263-265.ZHOU J P，YANG X H，ZHENG Y P.Check of Vibration Signals for Turbo-generator Units Based on Wavelet Analysis［J］.Journal of Shanghai University of Electric Power，2008，24（3）：263-265.

［6］张斌，王彤，谷传纲，等.基于小波分析后台阶流动中的湍动能能谱分布［J］.上海交通大学学报，2008，42（8）：1 221-1 225.ZHANG B，WANG T，GU C G，et al.Turbulent Energy Spectra Distribution in Backward Step Facing Flow Based on Wavelet Analysis［J］.Journal of Shanghai Jiaotong University，2008，42（8）：1 221-1 225.

［7］吴中.波浪研究中的多分辨方法［J］.海洋工程，1999，17（1）：62-70.WU Z.Multi-resolution Analysis in Wave Study［J］.The Ocean Engineering，1999，17（1）：62-70.

［8］冯卫兵，任华堂，洪广文.上海海域风浪谱分析与研究［J］.河海大学学报，2002，30（3）：28-32.FENG W B，RENG H T，HONG G W.Representation of Sea Wave Spectra for Shanghai Seas［J］.Journal of Hohai University，2002，30（3）：28-32.

［9］邵利民，袁群哲，俞聿修.波浪反射系数谱的特征分析［J］.海洋学报，2005，27（5）：157-163.SHAO L M，YUAN Q Z，YU Y X.Analysis characteristics of wave reflection coefficient spectrum［J］.ACTA Oceanologica Sinica，2005，27（5）：157-163.

［10］俞聿修.不规则波浪的观测与试验［J］.港工技术，1999（1）：1-5.YU Y X.Observation and Experiment of Irregular Waves［J］.Port Engineering Technology，1999（1）：1-5.

［11］吴克俭，宋金宝，楼顺里.论风浪的局域结构—风浪的局域结构与局域小波能谱［J］.海洋与湖沼，1998，29（4）：403-408.WU K J，SONG J B，LOU S L.Local Structures of Wind Waves I.Local Structures of Wind Waves and Local Wavelet Energy Spectrum［J］.Oceanologia ET Limnologia Sinica，1998，29（4）：403-408.

［12］吴克俭，宋金宝，楼顺里.论风浪的局域结构—风浪局域小波能谱的性质及应用［J］.海洋与湖沼，1998，29（5）：488-493.WU K J，SONG J B，LOU S L.Local Structures of Wind Waves II.Properties of Local Wavelet Energy Spectrum and its Applications［J］.Oceanologia ET Limnologia Sinica，1998，29（5）：488-493.

［13］常云华，李宗伟，尹大娟.非平稳振动信号的小波分析方法［J］.噪声与振动控制，2008（5）：98-101.CHANG Y H，LI Z W，YI D J.Study on the Wavelet Analysis for Non-Stationary Vibration Signal［J］.Noise and Vibration Control，2008（5）：98-101.