大范围波浪传播数学模型

杨耀中，冯卫兵

（河海大学海洋学院，南京210098）

南黄海辐射沙脊群位于浅海区，海域开阔，有折射、绕射、破碎等波浪现象。为了研究波浪机理，科研人员开发出大量的波浪浅水变形数学模型［1］。一般说来，可按照计算水域的范围，把数学模型划分为小、中、大三类。第一类是小范围模型，以三维N-S方程为代表。此类模型可以求解完整的三维N-S方程，具有精度高的特点［2-3］。但由于计算机容量和速度的限制，目前以小范围应用为主。第二类是中等范围模型，以Boussinesq方程和Berkhoff缓坡方程为代表。Boussinesq方程描述的是波面随时间的变化过程，在数值求解时一般时间步长取周期的1/24～1/30，空间步长取波长的1/8～1/12。因此此类方程只适合于中等范围计算，如港池内波浪场的计算［4］。同样Berkhoff缓坡方程由于待求量为波势函数，需要在一个波长范围内布置8～10个计算点，因此在有限的内存条件下，计算范围也受到限制［5］。第三类是以动谱平衡方程为代表的大范围模型。此类模型虽然可以计算大范围波浪场，但前提条件是加大空间步长，降低网格分辨率［6］。而辐射沙脊群海域面积十分广阔，达到140 km×200 km，同时地形变化剧烈。用加大空间步长的方法计算很可能造成模拟结果失真。鉴于此，本文建立了大范围、细网格波浪折射、绕射数学模型。

1 推广的缓坡方程

本文在洪广文推导的缓坡方程基础上建立了模型［7］。洪广文在传统的缓坡方程中引入波数矢无旋性假定，把定常缓坡方程转化为波作用方程和光程函数方程。这样就把求解随空间快速变化的波动势函数转化为变化较慢的波作用和波数，使得求解缓坡方程时，空间步长只取决于海底地形变化的剧烈程度，而不受波长条件限制，增大了数学模型的计算范围。

弥散方程

式中：ω为绝对频率；g为重力加速度；k为波数；h为水深；W*为底摩阻能量损耗项。

波数矢无旋性方程

式中：K为波数矢；α为波浪传播方向。

波作用守恒方程

光程函数方程

2 数值求解

波数矢无旋性方程和波作用守恒方程均属于非线性双曲型偏微分方程，需要选取一种有限差分格式进行数值求解。本文采用后差分半隐格式，运用这种差分格式编写源代码时，可以把方程对内存的需求转换为对硬盘的需求，从而大幅度提高计算范围和网格分辨率。本文称此方法为硬盘同步记录法，适合计算像辐射沙脊群这种范围大、网格分辨率要求高的海域。

2.1 硬盘同步记录法

篇幅所限，这里仅以式（2）为例进行有限差分，说明硬盘同步记录法的实现过程，其他方程解法类似。运用后差分半隐式法，对式（2）进行离散可得

式中：K、αi-1，j、Δx、Δy 为已知量；αi，j-1、αi，j、αi，j+1为未知量。式（5）属于非线性双曲型方程，用迭代法对其求解。由离散格式可以看出，只要知道 αi，j就可以求出 αi+1，j，αi-1，j的值不参与计算。这样可以把 αi-1，j记录到硬盘，同时释放内存。按以上步骤编程就可以用硬盘代替内存记录数据，从而实现硬盘同步记录法，达到用高分辨率网格计算大范围波浪场的目的。

2.2 初始条件和边界条件

直接给定初始条件为外海原始波高H0、波周期T和波向α0。波高边界条件

波向边界条件

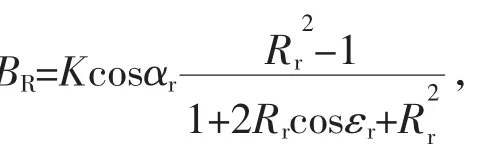
波浪破碎指标为0.78H。

3 数学模型的验证

为了检验本数学模型模拟波浪传播变形的精确程度，采用Whalin［8］的物理模型实验值与数学模型计算值进行比较。实验用的水槽长25.5 m，宽6.096 m，水深分布如图1所示，且可以用下式表示

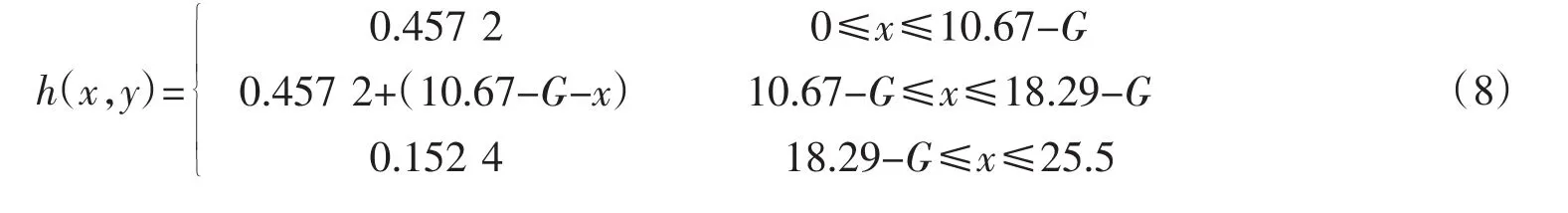
式中：G（y）=［y（6.096-y）］1/2，0≤y≤6.096。

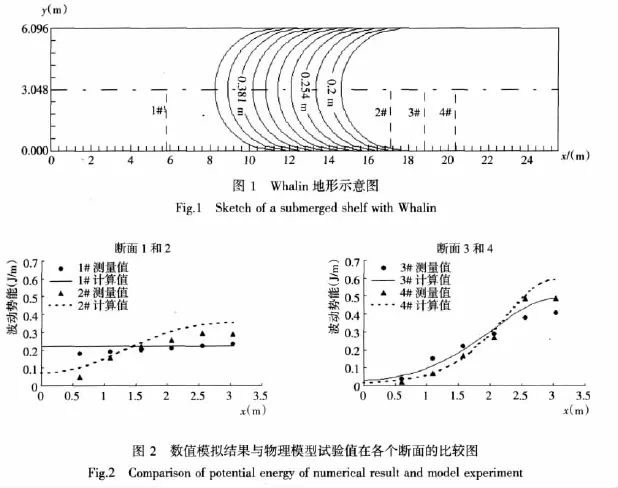
试验条件为波周期1 s，波高0.019 m。波浪入射方向为x向，其空间步长为0.05 m，y方向空间步长为0.122 m，侧边界为全反射。在x轴5.8 m、17.0 m、18.76 m、20.15 m处，设置了4个测量断面，用以获得波高信息。图2表示4个断面的能量分布，由图2可见数学模型与物理模型实验值能较好地吻合，模型的精确程度令人满意。

4 数学模型在辐射沙脊群海域的应用

4.1 数学模型在辐射沙脊群的适用性

辐射沙脊群海域范围广阔、地形复杂。它是呈辐射状分布的出露于海面以上的沙洲与隐伏于海面以下的沙脊及其潮流水道的总称。其地理位置处于江苏岸外，黄海南陆架海域。北起射阳河口，南至长江口北部的蒿枝港，南北长200 km，东西宽140 km。其水下地形十分复杂，大致以 港为顶点呈褶扇状向海辐射（图3）。由70多条沙脊和潮流水道组成，脊槽相间分布，水深介于0～25 m。分割沙脊的潮流水道主要有西洋、小北槽、陈家坞槽、草米树洋、苦水洋、黄沙洋、烂沙洋、小庙洪等。这些大型的潮流水道，水深均大于10 m，深度向海递增。

图3用25个标号点表示出8条主要潮流水道。同时为了方便讨论各个潮流水道内波浪场分布情况，把辐射沙脊群海域分成3块区域。

计算辐射沙脊群波浪场所需网格数巨大，所以有必要使用硬盘同步记录法。首先辐射沙脊群范围广阔，使得计算域面积大。其南北范围介于 32°00＇N，33°48＇N，长达199.6 km，东西范围介于 120°40＇E～122°10＇E，宽度为140 km。其次水下地形变化剧烈，对网格分辨率要求高。在地形变化剧烈的海域，实测点距离小于30 m才能准确反映出地形的起伏。因此如果网格步长大于30 m则不能精确反映地形的变化。

综上所述，由于辐射沙脊群范围大、地形变化剧烈，为了准确计算波浪场，需要按照x×y=140 km×200 km，dx×dy=30 m×30 m确定模型。这使得计算所需要的网格数巨大，超过了32位Fortran编译器能够编译的范围。如果采用硬盘同步记录法则可以解决此问题。

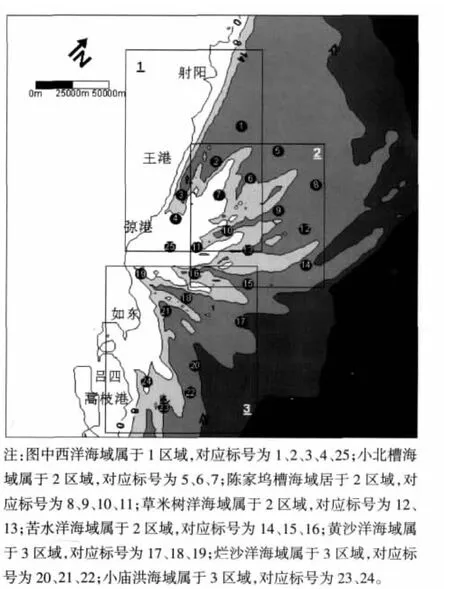
图3 辐射沙脊群地形图Fig.3 Relief map of radiative sandy ridge field

4.2 辐射沙脊群海域波浪场特征分析

应用上述数学模型计算了辐射沙脊群海域波浪场。根据对此海域波况的观测统计，本海区常年多出现NE向浪。限于篇幅，这里只给出NE方向平均潮位下，平均情况下波浪场的情况。

平均情况下的波浪场由于其出现频率高，所以对辐射沙脊群海底地形的演变和冲淤平衡具有重要分析价值。本文取平均年最大风速对应的有效波高2.64 m［9］为平均情况下的波浪场计算原始条件。这里的平均年最大风速相当于2 a一遇的风速。由于平均潮位历时长，波浪在此条件下对辐射沙脊群地形的作用时间也长，因此对地形的演变和冲淤平衡具有重要分析价值。下面将以T=8 s，Ho=2.64 m作为分析探讨沙脊群海域波浪场特征的原始条件，对平均潮位时波浪场各个特征进行分析。

4.2.1 等波高线呈弧形分布

图4实线表示1 m等波高线，虚线表示2 m等波高线。由图4可以看出1 m等波高线环绕辐射沙脊群顶点弶港，呈弧形分布。在岸线与1 m等波高线之间形成范围较大的、波高较小的掩蔽区。2 m等波高线环绕辐射沙脊群顶点弶港，呈锯齿形分布。锯齿形表示此片海域波高多为2 m。

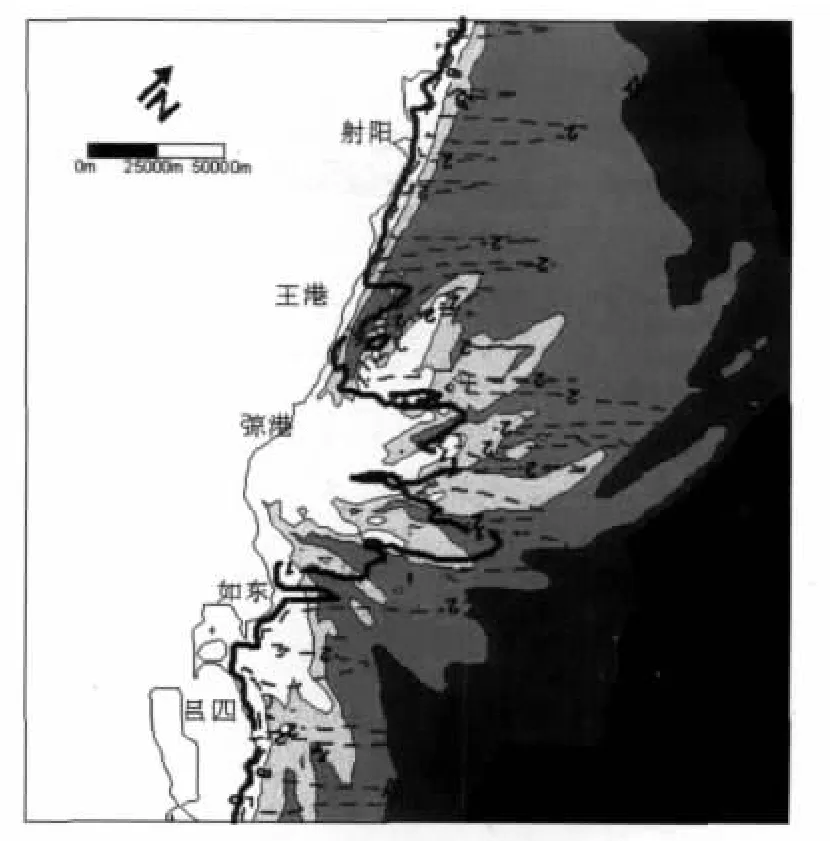
图4 辐射沙脊群海域等波高线分布Fig.4 Isoline of wave height in radiative sandy ridge field

为了清晰地表示出潮汐通道内波高分布情况，在沙脊群间8条主要潮汐通道深槽中布置计算点25处，并将计算点连成等波高线（图5）。其中细实线表示1 m等 波高线，粗实线表示2 m等波高线。由图5可以看出在岸线与1 m等波高线之间形成范围较大、波高较小的掩蔽区。这种独特的波高分布状态的形成是由于等水深线同样大致呈弧形分布。弶港东侧沙脊群顶点附近海域水深较小，波浪由外海传来，由于多次破碎，波能消耗，波高减小。而弶港南北两侧水深较大，波浪传至近岸海域，才会发生破碎，波高减小。因而形成了等波高线弧形分布的特征。

4.2.2 波浪多次破碎

波浪处于破碎状态时，水体的紊动与漩涡非常强烈。破碎带是波能的主要消耗区域，也是海滩上泥沙运动最剧烈的地方。因此研究破波带对辐射沙脊群的演变和冲淤平衡具有重要的分析价值。

图6中近岸黑色区域是波浪的破碎点，灰色轮廓线是破波带的外缘。由图6可见，弶港东侧海域破波带外缘比其他海域离岸线要远。这主要是由于水下存在巨大的沙脊，使得该处水深较小。同时此海域属于辐聚区，能量聚集使得波高增大。当波高增大到一定程度，就产生了破碎现象，因此该海域破碎带距离岸线比较远。

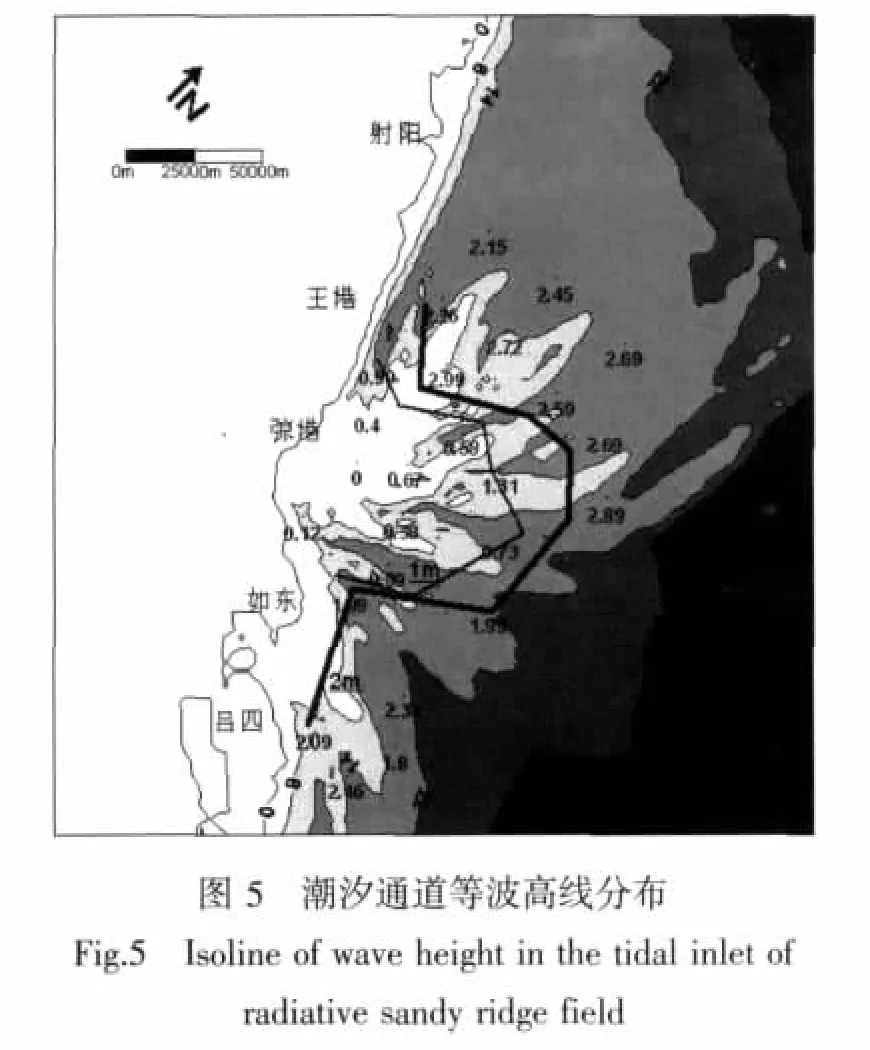
图6 辐射沙脊群海域破波带分布Fig.6 Surf zone of radiative sandy ridge field

随着波浪传播到近岸，又多次破碎，能量迅速减小，波高逐渐降低，在近岸海域形成范围较大的、波高较小的掩蔽区。所以波浪多次破碎是辐射沙脊群响应波浪场的重要特征之一。

4.2.3 以黄沙洋为界分为2个特征相异的波浪场

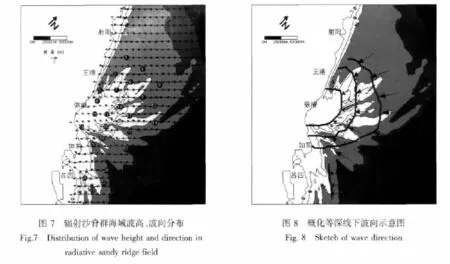
由图 7可见，西洋（1～4号点）、陈家坞槽（8～11号点）、草米树洋（12、13号点）、苦水洋（14～16号点）、黄沙洋（17～19号点）的波向随着波浪向岸传播逐渐转向弶港。这主要是因为该片海域等深线总体上呈以弶港为圆心的弧形分布（图8）。其中黑色曲线表示概化的等水深线。由于地形对波浪的折射作用，波向线将集中，从而产生辐聚现象。波向线沿垂直于等深线方向传播，于是形成了波向线以弶港为顶点呈辐射状分布的现象。而烂沙洋（20～22号点）、小庙洪（23、24号点）海域波向并没有明显转向弶港，这同样是因为水深的折射作用。波浪受地形的折射影响，沿着与等深线垂直的方向传播，而该海域等深线较为平顺，总体上与岸线走向一致，所以波向线表现出垂直于岸线传播的特征。

由以上分析可以看出地形对波向影响明显。在黄沙洋以北地区，地形呈明显的辐射状，波浪受其影响转向明显。而在黄沙洋以南地区，由于深水区的入射波浪从NE方向入射，波峰线与等深线大体平行，同时这些位置水深较大，所以波向偏转较小。

5 结论

黄海辐射沙脊群海域范围广阔，水下地形复杂，本文提出的波浪数学模型同时兼顾了大范围和细网格的要求。模型通过硬盘同步记录法，把数值求解时所需要的内存用量转化为硬盘用量，同时大幅度提高了计算范围与网格分辨率。与N-S方程、Boussinesq方程、缓坡方程相比，本模型能够计算大范围波浪场；与动谱平衡方程相比，本模型能够用细网格计算大范围波浪场。同时为了反映剧烈变化的地形对波浪场的影响，还引入了高阶地形变化影响因子，使模型计算精度进一步提高。综上所述，本模型适合计算超大范围下复杂地形波浪场。

模型在辐射沙脊群计算结果表明：

（1）在平均潮位下，外围深水波浪传播进入沙脊群海域，由于水下地形阻碍作用，等波高线环绕辐射沙脊群顶点弶港呈弧形分布。

（2）在黄沙洋以北的潮汐通道中，波向变化显著，大体指向弶港方向，而黄沙洋以南波峰线与岸线基本平行。

（3）随着波浪进入沙脊群顶点附近的浅水区，多次发生破碎，波能不断消耗，波高逐渐减小，在近岸形成了范围较大的掩蔽区。

［1］刘海成，刘海源，杨会利.近岸波浪变形数值模型的比较研究［J］.水道港口，2009，30（3）：153-158.LIU H C，LIU H Y，YANG H L.Comparison of numerical models of nearshore wave transformation［J］.Journal of waterway and harbor，2009，30（3）：153-158.

［2］ZHAO L H，LI T C.Fractional-step finite element method for calculation of 3-D free surface problem using level set method［J］.Journal of Hydrodynamics：Series B，2006，18（6）：742-747.

［3］WU C H，YUAN H L.Efficient non-hydrostatic modeling of surface waves interacting with structures［J］.Applied Mathematical Modelling，2007，31（4）：687-699.

［4］FUHRMAN D R，MADSEN P A.Simulation of nonlinear wave run-up with a high-order Boussinesq model［J］.Coastal Engineering，2008，55：139-154.

［5］JIN H，ZOU Z L.Hyperbolic mild slope equations with inclusion of amplitude dispersion effect：regular waves［J］.China Ocean Engineering，2008，22（3）：431-444.

［6］XU F M，Will P，ZHANG J L，et al.Simulation of typhoon-driven waves in the Yangtze estuary with multiple-nested wave models［J］.China Ocean Engineering，2005，19（4）：613-624.

［7］HONG G W.Mathematical models for combined refraction-diffraction of waves on non-uniform current and depth［J］.China Ocean Engineering，1996，10（4）：433-454.

［8］Whalin R W.Wave refraction theory in a convergence zone［C］//Coastal Engineering Research Council.Proc.13th Int.Conf.Coastal Engineering.Vancouver：ASCE，1972：451-470.

［9］张东生，张君伦，张长宽，等.潮流塑造-风暴破坏-潮流恢复-试释黄海海底辐射沙脊群形成演变的动力机制［J］.中国科学：D辑，1998，28（5）：394-402.ZHANG D S，ZHANG J L，ZHANG C K，et al.Tidal current work-surge destruction-tidal current restoration：A preliminary study on the dynamic mechanism of the development of the radical submarine sand ridges of the South Yellow Sea［J］.Science in China：Series D，1998，28（5）：394-402.