IXSea Gaps超短基线定位数据卡尔曼滤波研究

王崇明，田春和，隋海琛

（交通部天津水运工程科学研究所，天津300456）

法国IXSea公司研制的新型超短基线（USBL）定位系统Gaps（Global Acoustic Positioning System）是世界上首个便携式、即插即用、无需坐标校准的超短基线定位系统，近年来引起了广泛的关注。其最大的优势是将GPS定位系统、惯性导航系统、光纤罗经/姿态仪系统同水声定位系统的传感器组装在一起，各传感器之间的相对偏移量在出厂前已进行内部标定并固化在系统的内部程序中，因此系统在现场无需标定，不存在各传感器之间的安装、测量误差问题，确保了系统的高精度导航定位。Gaps采用宽频发射信号，在增大作用距离的基础上，提高了定位精度。最大有效距离为4 000 m，定位精度达到斜距的0.2%，角度精度为0.12°，距离精度最高可达0.2 m，能最大限度地满足近距离水下定位及导航的要求［1-2］。除此之外，系统可以同时追踪多个水下目标［3］。在海洋工作环境中，由于噪声影响产生的USBL定位误差甚至粗差是不可避免的。Gaps也存在同样问题，由于信标的运动轨迹是有章可循的，不会产生较大的突起，运动轨迹相对平滑，这样就可以应用卡尔曼滤波剔除错误点。本次水下超短基线定位即使用IXSea Gaps系统进行数据采集。

1 卡尔曼滤波的基本原理

卡尔曼滤波是一种最优化自回归数据处理算法，它通过不断预测、修正递推过程，可随时计算最新的滤波值，便于实时处理观测数据，提供一种最优估计值。

经典卡尔曼滤波应用的一个先决条件是建立准确的动态模型和观测模型，这就要求较清楚地了解物体的运动。偏离理想假设的观测向量或动力学模型必然会给动态定位结果带来偏差，甚至导致卡尔曼滤波发散［4］。

本次动态定位试验采用定常速度模型，状态方程和测量方程都是线性的，状态向量X（k）选取坐标和速度，加速度为状态噪声W（k）

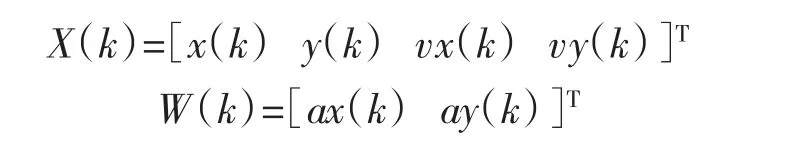
式中：x（k），y（k）为 k 时刻信标的坐标；vx（k）、vy（k）为 k 时刻信标的速度；ax（k）、ay（k）为 k 时刻信标的加速度。

设状态方程和测量方程都是线性的，则可以建立如下方程

状态方程

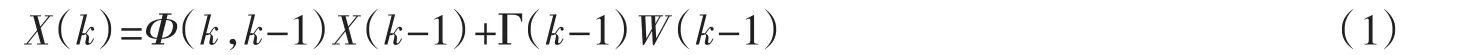
观测方程

式中：Φ（k，k-1）为状态转移矩阵；Γ（k-1）为动态噪声干扰矩阵；H为测量矩阵；P（k）为观测值矩阵；V为测量误差。

根据测量误差理论及限差要求，设此线性系统满足下列条件

在此次超短基线定位试验中，分别选取

式中：t（k）为数据采样时间间隔。

信标的运动轨迹相对平滑，且每一时刻的位置具有唯一性，因此可以对其进行卡尔曼滤波。根据最小方差无偏估计原理，导出卡尔曼数据滤波的递推方程如下。

一步预测值

预报误差方差阵

滤波增益矩阵

滤波值

滤波误差阵

式中：I为单位阵。

首先需要确定状态和观测噪声的初始方差，即Dw（k，k-1）和Dv，可根据经验选取。若信标随时间变化缓慢，则Dw（k，k-1）取值较小，表明模型变化比较缓慢［5］，这样得到的滤波值结果就比较平坦；若信标运动速度变化较大，则Dw（k，k-1）取值相应要变大。Dv的取值应与测量值的方差相对应，当测量值有较大的方差时，Dv的取值相应较大。初始速度可以由前2个观测值来确定，状态噪声和观测噪声的初始方差分别取0.005和1.5。当滤波对象发生变化时，模型参数也应该进行相应的调整，以达到最佳的滤波效果。

2 卡尔曼滤波的特点

卡尔曼滤波方程是一组递推计算公式，其计算过程是一个不断预测、修正的过程。求解时不需要贮存大量的观测数据，且当得到新的观测数据时，可随时算得新的滤波值，便于实时处理观测成果。

卡尔曼滤波还具有以下特点：增益矩阵与观测值无关，因此可以预先算出，从而减少实时处理的计算工作量；增益矩阵与Dv成反比，与Dw成正比；卡尔曼滤波方程是根据广义最小二乘原理导出的，而按广义最小二乘原理得到的结果具有无偏性和方差最小性，因此卡尔曼滤波值是由观测值得到的最小方差无偏估计，其误差方差阵就是所有估计中的最小方差阵［6］。

3 野值的判别

测量中的误差是不可避免的，在海洋测绘中海洋噪声、工作环境以及仪器设备安装等均会使测量数据产生较大误差，即野值。在进行数据处理时必须将其删除，否则会严重影响精度，甚至导致滤波器发散。

在卡尔曼滤波器中，残差 Δ（k）=P（k）-X（k/k-1），它是一个零均值的高斯随机量，其协方差阵为 S（k），利用残差的统计特性，采取强约束的方法，可以得到如下野值判定准则

若式（8）成立，则认为观测值P（k）正确，否则视观测值为野值，当出现野值时，不考虑实际测量值，将观测预报值作为最终结果。

4 定位实验与数据处理

在此次定位试验中，将信标放置于运动的船上，Gaps安置在一固定位置进行数据采集。根据上述原理，编写程序实现了适用于超短基线定位数据的卡尔曼滤波。

原始观测数据是带有随机误差的数据，并且有些数据还带有较大误差，即所谓的野值，这会严重损害测量结果的精度（图1）。

图2为经卡尔曼滤波后的数据，可以看到滤波数据较原始数据更平滑。图3为滤波数据与原始数据的比较结果，可以看出两者较吻合。这说明卡尔曼滤波取得了良好的效果，明显改善了超短基线定位的结果。

5 结论

由于受到各种噪声的影响，用IXSea Gaps超短基线进行定位所得的观测数据中不可避免的带有一些误差。本文编程实现了超短基线定位的卡尔曼滤波，通过对原始观测数据进行卡尔曼滤波，得到了平滑且与原始观测数据较吻合的结果，说明卡尔曼滤波可以明显地改善超短基线的定位结果。

［1］李守军，包更生，吴水根.水声定位技术的发展现状与展望［J］.海洋技术，2005，24（1）：130-135.LI S J，BAO G S，WU S G.A Practical Overview and Prospect of Acoustic Positioning Technology［J］.Ocean Technology，2005，24（1）：130-135.

［2］吴永亭，周兴华，杨龙.水下声学定位系统及其应用［J］.海洋测绘，2003，23（4）：18-21.WU Y T，ZHOU X H，YANG L.Underwater Acoustic Positioning System and Its Application［J］.Hydrographic Surveying and Charting，2003，23（4）：18-21.

［3］杨鲲，吴永亭，赵铁虎，等.海洋调查技术及应用［M］.武汉：武汉大学出版社，2009.

［4］宋迎春.动态定位中的卡尔曼滤波研究［D］.长沙：中南大学，2006.

［5］郭纪捷.水下拖体声学超短基线定位测量及其卡尔曼滤波技术［J］.海洋技术，2002，21（1）：7-11.GUO J J.Location of a Tow body by Ultra-short Base Line Underwater Acoustic Positioning and Kalman Filtering［J］.Ocean Technology，2002，21（1）：7-11.

［6］崔希璋，於宗俦，陶本藻，等.广义测量平差［M］.武汉：武汉大学出版社，2001.