基于神经网络集的注射成型工艺参数多目标优化

胡泽豪,卫 炜,刘 娟,刘 琨

(中南林业科技大学机电工程学院,湖南长沙410004)

基于神经网络集的注射成型工艺参数多目标优化

胡泽豪,卫 炜,刘 娟,刘 琨

(中南林业科技大学机电工程学院,湖南长沙410004)

以计算机辅助工程(CAE)数值仿真正交试验所得工艺参数与质量指标的数据作为训练样本,对经过优化的BP神经网络进行训练,得到工艺参数与制品质量指标之间的神经网络集近似计算代理模型,该模型快速准确,有明确的数学公式,可以利用遗传算法进行全局寻优,得到使多个质量指标综合最优的工艺参数组合。通过对比验证,这种多目标优化方法可以在正交试验结果数据较少的情况下较大程度地提高制品的多个质量指标。

注射成型;工艺参数;神经网络集;多目标优化;代理模型;遗传算法

0 前言

目前,生产注射成型制品通常采用三维软件设计产品—设计模具—制造模具—生产的流程,设计人员只是凭经验设计模具,产品的品质全靠操作工的经验来调整工艺参数,即试错法,这种方法生产出的产品品质并不能保证是最优的,而且存在调试时间长、浪费严重等问题。

CAE的应用为工艺优化和模具设计的改进提供了极大的方便。用计算机模拟可以代替真实实验,判断出所用工艺条件的适用性,节省了时间和成本,但目前的应用也仅限于用CAE分析代替反复试模,这只能获得合理工艺而不是最优,且对于大型复杂的制品,由于工艺和制品模型的复杂性,CAE分析时间较长,不可能进行大量的仿真实验[1]。因此,有效利用CAE模拟结果,抽取信息建立合适的代理模型,借助于优化算法,对优化模具设计参数和成型工艺参数十分重要,可从根本上解决依赖经验及技巧的问题。随着计算机运算速度的提高和相关注射成型模流分析软件的发展,设计人员可以在模具设计出来后在电脑上进行注射成型过程的模拟分析,进而修改模具不合理的地方。

本文在此基础上进一步计算出最优的工艺参数组合,这也将是未来模流分析软件发展的趋势,即不只是对填充过程进行模拟,还要分析得出更加合理的各项参数。本文采用Moldflow软件对注射成型过程进行数值模拟计算,并使用BP人工神经网络结合正交试验设计方法建立注射成型过程的近似计算代理模型,进而运用遗传算法进行全局寻优,得出使制品各个质量指标综合最优的工艺参数组合。

1 注射成型质量指标的确定

注射成型质量指标主要可以归成力学性能、尺寸和其他可以观测到的指标,例如黑斑(材料有关的缺陷)、短注、沉降斑、层状组织、气穴(成型过程有关的缺陷)、尺寸变化、翘曲和制品质量(模具和成型条件有关的缺陷)等。

本文研究的对象是手机后框外壳,如图1所示,属于薄壳形注塑件,且制品厚薄不均匀,易有较大的翘曲变形和沉降,而且某些部位有较高的外观品质要求,同时有一定的装配要求。体积收缩率是聚合物材料线收缩率的定性表示,如果材料收缩是各向同性的,线收缩率近似等于体积收缩率的1/3。成型过程中制品在型腔中非均匀的体积收缩率是引起制品翘曲的主要原因,型腔中制品的体积收缩率变化(体积收缩率的最大值与最小值的差值)越小越好,即制品的体积收缩率越均匀越好。缩痕指数反映制品的表面品质,沉降斑被视为制品表面品质的退化,缩痕指数用于说明沉降斑受材料、零件几何特征、充模成型条件等影响的严重程度。翘曲变形是指注射成型制品从型腔脱模后由于制品内残余应力的存在而使制品的形状产生变形,它是注射成型制品最常见的缺陷之一。注射成型制品结构中壁厚不均和不对称,浇口位置、流道系统、冷却系统设计不当,成型工艺参数不合理等均会使注射成型制品收缩不均而产生翘曲变形。

图1 制品的3D实体模型Fig.13D solid model of the product

因此,根据产品设计要求和使用情况,本文选取体积收缩变化量、平均体积收缩率、缩痕指数、翘曲变形量作为注塑件的尺寸和外形精度、组织性能、表面性能和力学性能的考核指标,通过这些指标的量化分析来保证制品综合品质达到规定的要求。

但是在实际生产中,如果没有完备的检测设备,这些指标的量化数据很难得到;即使在设备齐全的情况下,对一些表观缺陷作定性与定量分析也有相当的难度。借助注塑模CAE软件进行数值仿真可以较准确地得到不同时刻型腔内塑料熔体的温度、压力和剪切应力分布,计算出制品的收缩情况和内应力的分布等,预测出实际试验难以测量的一些质量指标,从而指导工艺参数的选定。

2 正交试验获取样本数据

正交试验法是指依据数据的正交性(即均匀搭配),通过构造出的一套规格化的正交表来进行试验方案设计,是目前最流行的试验设计方法。用正交设计表安排试验,相对于全面试验而言,它只是部分试验,可用比全面试验法少很多的试验次数,获得能基本上反映全面情况的试验数据。

用正交表设计试验方案的程序为:(1)确定试验指标,明确试验目的,确定试验考核目标;(2)确定因子与水平,制定因素位级表;(3)选用正交表;(4)进行试验及结果分析。

2.1 正交试验设计

本试验的目标是寻求较好的工艺参数组合,以提高注射成型制品的综合品质。同时找出对每个指标有较大影响的主要因素,以指导工艺参数的调整。

考察指标选用体积收缩变化量、平均体积收缩率、缩痕指数和翘曲变形量4个指标的综合评价值。体积收缩变化量、缩痕指数和翘曲变形量的值越小,说明制品的品质越好,设计模具时注塑件的收缩率设为0.6%,设计公差等级为5级。实际生产中,模具温度、熔体温度、充模时间、保压压力、保压时间、冷却时间6个独立工艺变量对成型质量指标有影响,故选这6个变量为考察因素。根据CAE分析的工艺范围各因素取5个水平值,建立因素水平表,如表1所示。

表1 因素水平设置表Tab.1 Factors and its levels

因该试验为6因素5水平试验,可选用L25(56)正交表[2]。试验数据取自Moldflow软件的分析日志中制品在保压阶段结束后的结果摘要和翘曲变形分布图,如图2所示。其中,体积收缩变化量取结果摘要中体积收缩率最大值与最小值的差值;平均体积收缩率取结果摘要中体积收缩率平均值;缩痕指数取结果摘要中缩痕指数最大值;翘曲变形量取翘曲变形分布图中最大的变形值,正交试验结果如表2所示。

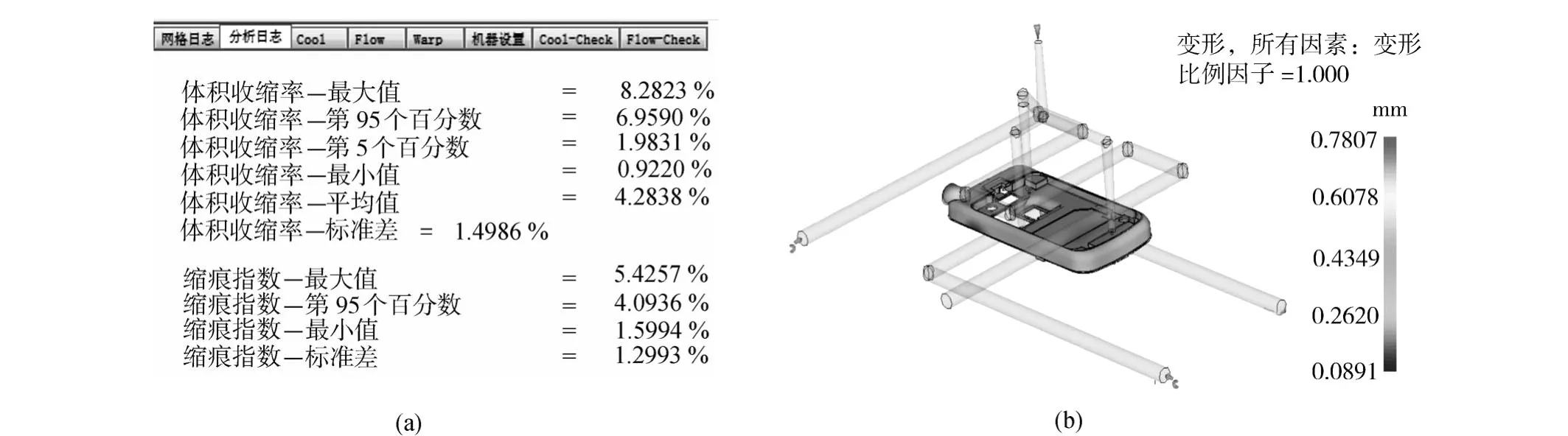
图2 制品的分析结果摘要和翘曲变形分布图Fig.2 Analysis results and distribution of warp deformation of the product

表2 正交试验结果Tab.2 Results of the orthogonal experiment

本文所选取的考核指标对产品品质的影响程度各有侧重,同时各参数的量纲并不一致,为兼顾各个指标,有必要建立一个使各个指标都尽可能好的综合评判方法,从而将多目标问题转化为单目标,实现多目标问题的综合优化。本文采用加权综合评分法进行评判,其中综合评分是根据模糊映射加权综合法得来的,计算公式如式(1)所示。

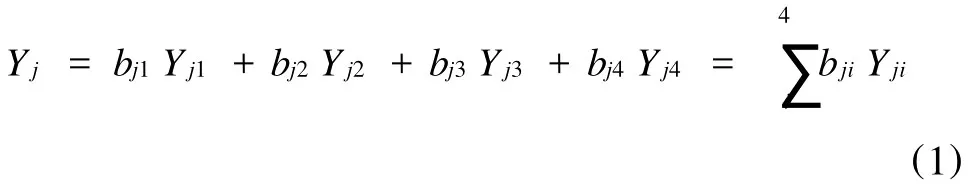
式中bji——权因子系数,表示第j个试验中第i项指标在加权综合评分中应占的权重

Yji——第j个试验中第i项考察指标

Yj——第j个试验中综合考察指标

为尽量使综合评分的结果合理,bji的取值十分关键。由于各指标值的范围不同,增加了权值bji确定的难度。鉴于对制品质量的评价本身含有一定的模糊语义,本文对式(1)中各质量指针采用模糊映像,以模糊集作为定量化的手段,将各指标值统一映射到[0,1]的数值空间。在模糊处理的基础上再对权值进行分配。权值分配根据正交试验分析结果和指针对制品综合品质的影响程度,按百分制加权,取bj1=25,bj2=20,bj3=25,bj4=30。

本文对具有双边约束的指针(如平均体积收缩率)采用双S形隶属度函数,对单边约束的指标(如体积收缩变化量、缩痕指数和翘曲变形量)采用S形隶属度函数,如式(2)所示。但由于本次试验中平均体积收缩率的试验结果值普遍大于设定的收缩率,因此也视为单边约束。参数a、c根据指标要求取不同的值,如表3所示。同时,通过调整隶属度函数中参数a、c,能使在合理范围的指标值得到较高的隶属度值,超出指标范围或一些明显坏的指标值通过映像后趋于较小的值或零。这样处理既方便了各权值的确定,又实现了对指标的约束,从而使综合评价的分值更趋合理。

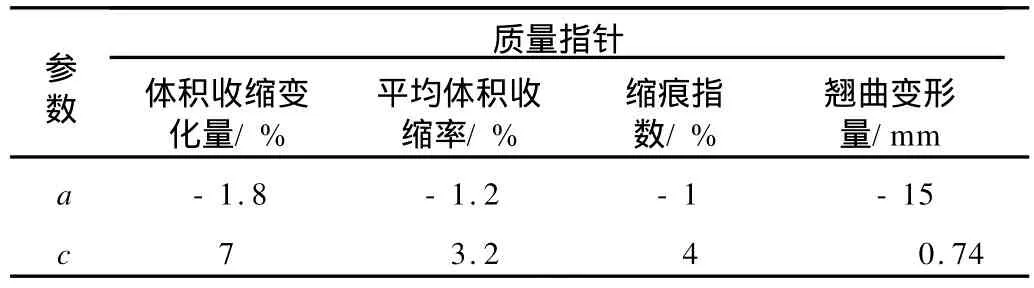
表3 指标模糊映射中的参数Tab.3 The parameters of target fuzzy mapping

2.2 试验结果的计算与分析

为得到各因素与指标的关系,找出指标随因素变化的规律和趋势,寻求各因素水平的最佳搭配,本文采用直观分析法,即计算出各因素在各水平上的平均值和极差。极差的大小反映了因素对指标的影响程度,极差大表明该因素对指标的影响大,通常为主要因素;反之,为次要因素。极差分析结果如表4所示,各个因素水平的影响趋势如图3所示。

表4 综合评分极差分析结果Tab.4 Range analysis results of the comprehensive score

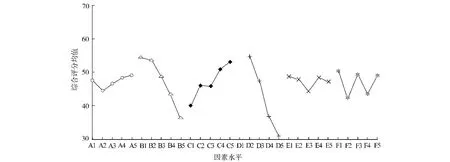
图3 各因素对综合评分的影响趋势Fig.3 Effects of the factors on the comprehensive score

通过对图3的分析,可以得到使综合评分值最高的工艺参数因素水平组合,即A5B1C5D1E1F1,将这组工艺参数组合带入Moldflow中进行验证,并与正交试验数据中综合评分值最高的组合进行比较,其结果如表5所示。

表5 正交试验指导参数配置的试验结果对比Tab.5 Comparison of the results

从两组试验的对比结果看,正交试验的方法在因素对单指标的优化中可以起到一定的指导作用,但是在多指标问题中如果存在因素变化对各个质量指标的作用效果不一致时,定性分析就较为困难。通过对指标的模糊加权综合处理,将多指标多目标问题转化为单一指标不仅是必要而且是必须的。同时,从对比试验结果看,在非线性系统、因素变化存在耦合关系和多指标综合评定情况下,正交试验的分析结果能对因素的配置起到较好地指导作用。

经过正交试验法分析,可以得到一个相对优秀的工艺参数组合,但这个组合并不是最优组合,因此还需要其他方法来获得最优值。建立近似计算代理模型即是本文运用的数学优化方法。为了提高改模型的精度,需要更多的数据样本,因此又进行了一组正交试验,各个工艺参数水平值与第一组不同,但参数设置范围与第一组基本一致,因素水平设置如表6所示,获得25组试验数据。此外,为了确认代理模型是否精确,又随机抽取15组工艺参数进行Moldflow分析,获得结果以用于验证模型精度。

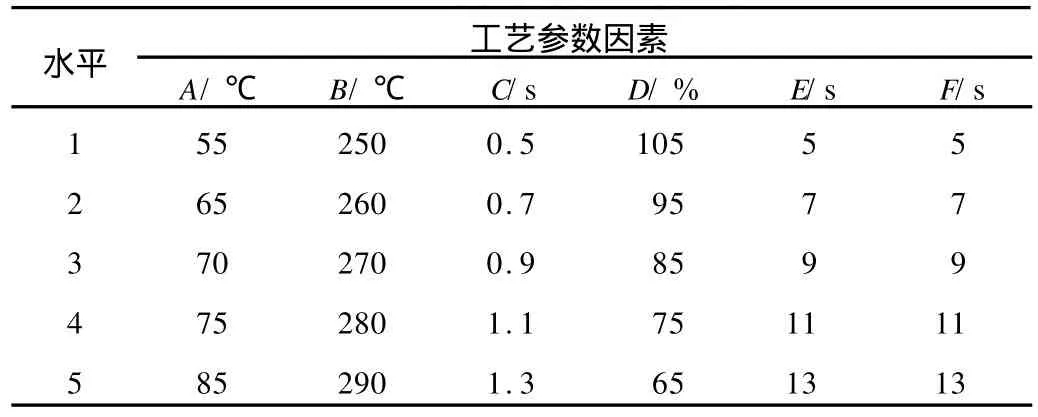
表6 第二组正交试验因素水平设置Tab.6 Factors and their levels for the second setting

3 近似计算代理模型的建立

由于注射成型过程的复杂性和高度非线性,传统的优化方法无法使用;CAE模拟软件只是按照假设与简化过的聚合物熔体在型腔中的黏性流变力学和热力学等公式对塑料制品的有限元模型进行逐步计算得到结果,求解过程计算量大,而且过程繁琐。因此,建立一个可以代替注射成型过程,描述工艺参数与制品质量指标之间映射关系,且有明确计算公式的代理模型,将会对注射成型工艺参数的优化起到很大帮助。

神经网络[3]建模不需要过程的先验知识,只根据过程的输入输出数据就可直接建模,且能逼近任何非线性映射。这种不精确依赖过程的数学模型特点使其在处理复杂系统的建模问题上具有独特的优越性。因此,很适合描述注射成型制品质量与工艺参数之间的复杂关系。神经网络有多种形式,其中误差反向传播神经网络(Back-Propagate,BP)模型是近年应用最广泛的网络之一。

3.1 BP神经网络输入输出参数确定

输入输出参数是建立神经网络过程中的关键环节。参数的选择应当既反应被模仿系统的行为规律,又力求简洁。根据所研究对象的设计要求和使用情况,本文选取正交试验结果的体积收缩变化量、平均体积收缩率、缩痕指数、翘曲变形量作为塑件的尺寸和外形精度、组织性能、表面性能和力学性能的考核指标,通过这些指标的量化分析来保证制品综合质量达到规定的要求。

3.2 BP网络学习样本的获取

在网络结构确定之后,学习样本的选择也是至关重要的,充足而正确的学习样本才能够正确反映系统的性能。由正交试验的设计原则可知,正交试验是依据数据的正交性(即均匀搭配)通过构造出的一套规格化的正交表来进行试验方案设计,正交试验不会漏掉主要因素的各种可能搭配,这被称为正交试验的整齐可比性,因此选择正交试验的结果作为训练样本,可以满足BP网络训练对样本代表性的要求。

本文通过CAE软件的Moldflow,模拟实验获得不同条件下的学习样本,通过正交试验与数值模拟得到的实验数据作为训练样本。为了研究学习样本数量多少对BP神经网络训练能力和泛化能力的影响,又进行了一组正交试验,各个工艺参数水平值与第一组不同,但参数设置范围与第一组基本一致,因素水平设置如表6所示。

3.3 BP神经网络对比试验

本文所建立的BP神经网络有6个输入,4个输出,为了观察神经元个数对神经网络学习能力和泛化能力的影响趋势,本文在Matlab中编写了BP神经网络的循环程序,神经元个数由1个逐渐增加到20个。考虑到每次神经网络训练初始化的权值与阈值都是随机生成的,因此得到的结果可能都不相同,循环程序又增加了网络训练次数,即每次选择一个神经元个数后,进行40次网络训练,得到所对应的神经元个数下的平均测试误差平方和。

本文共进行了2组6因素5水平正交试验,一共有50组训练样本,这组为多训练样本。另外,抽取第一组正交试验的结果,25组训练样本,这组为少训练样本。通过试验,得到样本数量对网络训练及泛化能力的影响。

本文又进行了15次Moldflow分析,作为测试样本对训练好的BP网络的泛化能力进行测试。测试样本的参数组合数值一部分在正交试验中出现过但不包含在正交试验方案设计中的组合,有些则为新样本,对于多训练样本的神经网络,有5组测试样本为未知样本;对于少训练样本的神经网络,则有10组测试样本为未知样本。

算法对网络学习能力的影响很大,因此选择一个合适的学习算法非常重要。本文对Levenberg-Marquardt算法和贝叶斯正则化算法进行了对比试验。

由于神经网络是一种基于梯度法的局部寻优算法,局部寻优能力很强,网络倾向于在初始权值和阈值附近找到局部最优点。在这种情况下,惟一的办法就是重新设置初始权值,再次进行搜索,但是这种方法始终不能保证得到全局最优权值。遗传算法(简称 GA)是群体寻优,不是从一个点开始,而是从许多点开始搜索。这种搜索具有全局性,因而可以防止搜索过程收敛于局部最优解,容易找到全局最优解或是性能很好的次优解。因此本文还研究了遗传算法对网络泛化能力的影响,用遗传算法优化神经网络权值的主要思想是改善神经网络的初始权值,适应度函数采用误差函数,如式(3)所示。

式中 sol——种群中的每个个体

xi——神经网络的实际输出

t——种群中的个体数

yi——神经网络的期望输出

实际输出与期望输出之间的差值越小,适应度函数值就越大。将得到的最优解,即误差最小的一组神经网络权值和阈值作为神经网络的初始权值进行训练,若不能满足精度要求,可再次进行神经网络训练。因为经过了遗传算法的全局搜寻,所以再次陷入局部极小值的可能性不大。反复训练,直到得到一组满足精度要求的神经网络权值和阈值为止。

综上所述,本文设计了8组试验,如表7所示。

表7 神经网络实验方案Tab.7 Experimental program of the neural net

神经网络训练完成后用测试集测试该网络的泛化能力,即计算测试样本的实际值与该网络输出值的误差平方和,误差平方和越小说明网络的泛化能力越强,为了观察得更加清楚,将所得的误差平方和被一除后再加平方,值越高说明这个网络的误差平方和越小,泛化能力越强,得分公式如式(4)所示。

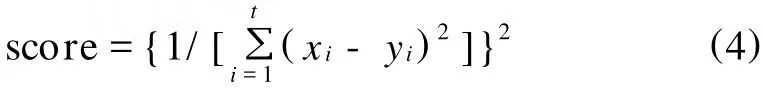
式中xi——测试样本神经网络的实际输出

t——测试样本的个体数

yi——测试样本的实际值

本文对上述8组试验的结果进行总结,结果如表8所示。

表8 神经网络模型对比实验结果Tab.8 Experimental results of the neural net model

由试验结果对比可知,Levenberg-Marquardt算法运算速度快,收敛快,但网络的泛化能力不高,而且训练样本数量多少对其有很大的影响;贝叶斯正则化算法运算速度慢,但能显著提高网络的泛化能力,并且训练样本数量多少对其影响不大,甚至训练样本数少时,网络的泛化能力可能更好;采用遗传算法优化网络的初始权值和阈值也能显著提高网络的泛化能力,但由于加入遗传算法寻优过程,运算时间更长。在实际生产中,应根据实际需要、运行平台、在线训练还是离线训练来合理选择组合。由对比试验结果可知,使用遗传算法优化网络初始权值和阈值,并采用贝叶斯正则化算法进行网络训练,可以在训练样本较少的条件下提高网络的泛化能力,使网络的预测精度大大提高。

3.4 神经网络集的建立

神经网络集成是用有限个神经网络对同一个问题进行学习,集成在某输入示例下的输出由构成神经网络集成的各神经网络在此示例下的输出共同决定[4]。因为神经网络集成利用有限多个神经网络来共同解决某一问题,能以较小的运算代价显著提高网络系统的泛化能力。本文采用简单平均构造法,即求各个子网的输出值总和的平均值,这个值就是此神经网络集的输出。

本文选取6输入、4输出,具有一个隐含层的BP网络,并用遗传算法对神经网络的初始权值和阈值进行优化,学习算法选取贝叶斯正则化算法,不确定隐含层数目,而是建立循环程序,在隐含层数目计算经验公式[式(5)]所计算范围内选取测试集误差平方和小于0.55的所有网络组成神经网络集,以进一步提高网络的泛化能力,减少网络的预测误差。最后经过运算,共选取了8个BP网络组成神经网络集。

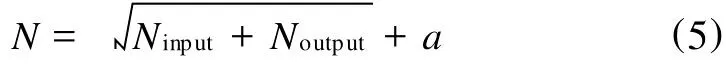
式中a——介于1～10的整数

前面8个BP网络的测试集误差平方和最小值为0.3051,而他们组成的神经网络集的测试集误差平方和为0.2628,可见泛化能力有了进一步的提高。该神经网络集的输出与实际测试样本的输出比较图如图4所示。

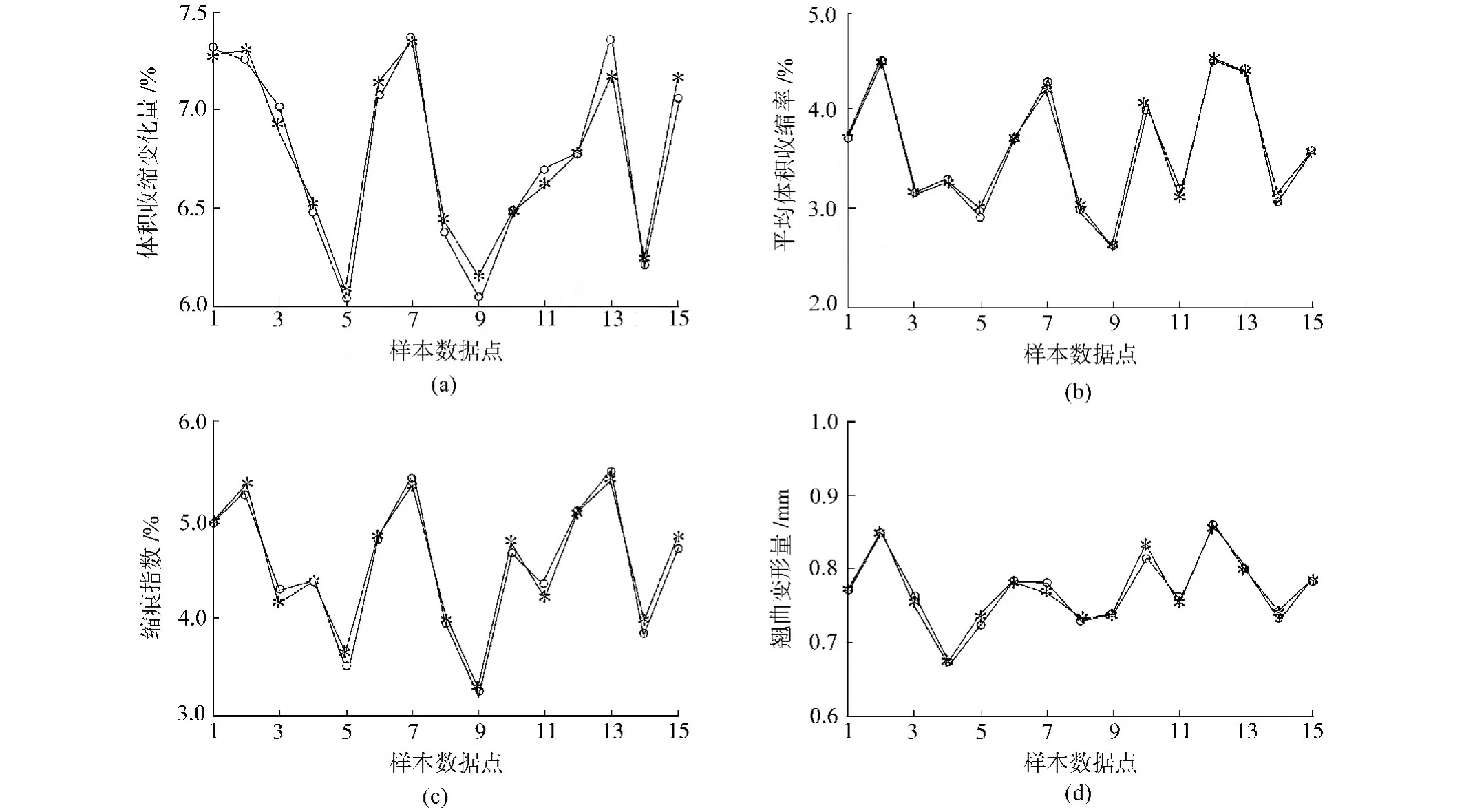
图4 简单平均法神经网络集输出与测试样本输出的对比Fig.4 Comparison between neural net output and the test sample output

由图4可见,神经网络集输出结果与数值模拟测试样本输出结果基本吻合,因此可以用来代替CAE数值模拟软件。

4 遗传算法全局优化获取最优工艺参数

上文已经得到注射成型工艺参数与制品各质量指标间的近似计算模型,虽然在此模型基础上,可以根据工艺参数的变化迅速而准确地预测出相应的指标值,但是由于工艺参数对质量指标的耦合影响,该模型并不能精确地指导工艺的最佳配置。所以,还需要运用智能优化技术进行工艺参数的综合寻优。

遗传算法[5]是基于自然选择和群体遗传机理的随机优化算法,是一种适用于复杂形态函数的全局寻优方法,而且由于搜索本质的并行性,遗传算法具有更高的效率。本节采用遗传算法实现注射成型的工艺参数多目标优化。

注射成型工艺参数多目标优化方法是指将神经网络集近似计算代理模型和遗传算法全局寻优相结合,以数值仿真正交试验为数据来源和分析手段,以注射成型工艺参数为变量,以质量的模糊加权质量综合评分函数为适应度函数,进行优化求解。

根据优化理论和对指标的模糊处理,本文的优化模型可表示为如式(6)～(8)所示。

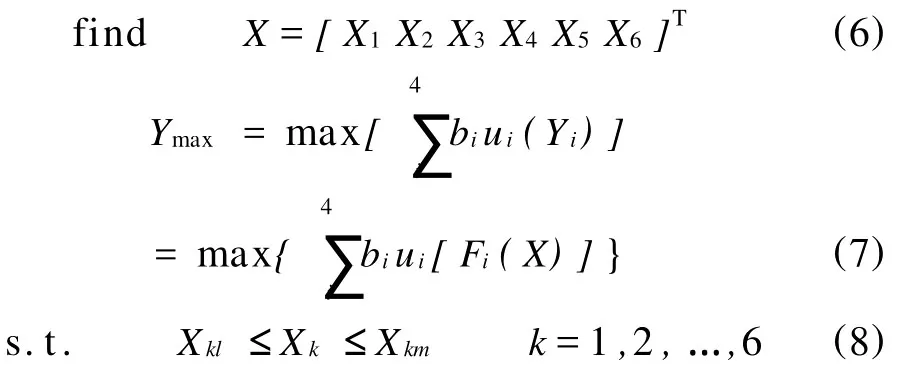
式中Fi(X)——工艺变量X对第i个指标Yi的近似计算式

ui(Yi)——第i个指标Yi的模糊映射

Xkl——第k个工艺变量的约束下限

Xkm——第k个工艺变量的约束上限

本文在Matlab平台上编写了神经网络集近似计算代理模型和遗传算法全局寻优结合的注射成型工艺参数多目标优化程序。初始种群数200,经过700代遗传进化,找到工艺参数的最优组合为:模具温度为50.1794℃、熔体温度为240.0041℃、填充时间1.3 s、保压压力为填充压力的 109.9951%、保压时间4.1482 s、冷却时间12.787 s。对应的质量指标为:体积收缩变化量5.4706%、平均体积收缩率0.8907%、缩痕指数1.4858%、翘曲变形量0.5560 mm,综合评分为93.6652。

采用Moldflow对遗传算法中得到的6个最优工艺参数进行验证,其质量指标结果为:体积收缩变化量5.7356%、平均体积收缩率0.9934%、缩痕指数1.7174%、翘曲变形量0.5690 mm,综合评分91.8921。

Moldflow验证的各项质量指标值与遗传算法所得的各项质量指标值相比误差已经很小,如表9所示,说明该近似计算代理的建立是成功的,并且经过比较可以证明运用该模型进行优化计算得到的最优工艺参数组合是最优秀的组合。

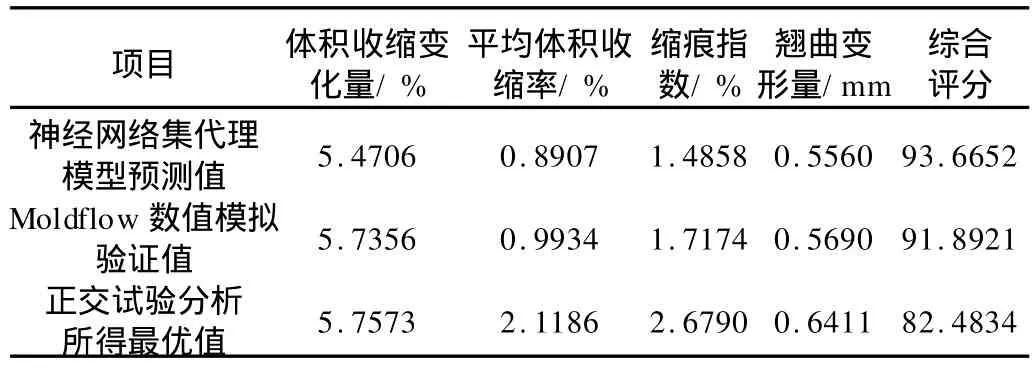
表9 结果对比Tab.9 Comparison of the results

由表9可知,Moldflow验证的各项质量指标值与正交试验以及经分析所得的结果相比较有所提高,其综合评分值(91.8921)比正交试验结果分析所得的最优结果(82.4834)也高出近10个数量值。

5 结论

(1)通过将注射成型过程中工艺参数对产品品质指标的影响进行量化,运用神经网络可建立模拟其关系的数学模型;

(2)运用遗传算法对该数学模型进行优化计算,可得出使产品各个品质指标综合最优的工艺参数组合为:模具温度50.1794℃,熔体温度240.0041 ℃,填充时间1.3 s,保压压力为填充压力的109.9951%,保压时间4.1482 s,冷却时间12.787 s。

[1] 申长雨,王利霞,张勤星.神经网络与混合遗传算法结合的注塑成型工艺优化[J].高分子材料科学与工程,2005,(5):23-27.

[2] 吴贵生,于治福,于淑政,等.试验设计与数据处理[M].北京:冶金工业出版社,1997:132-138.

[3] 飞思科技产品研发中心.MATLAB6.5辅助神经网络分析与设计[M].北京:电子工业出社,2003:55-60.

[4] 吴建鑫,周志华,沈学华,等.一种选择性神经网络集成构造方法[J].计算机研究与发展,2000,(9):1039-1044.

[5] 王小平,曹立明.遗传算法理论、应用与软件实现[M].西安:西安交通大学出版社,2002:23-28.

Multi-objective Optimization of Injection Molding Processing Parameters Based on Neural Networks Ensemble

HU Zehao,WEI Wei,LIU Juan,LIU Kun
(College of Mechanical and Electronical Engineering,Central South University of Forestry and Technology,Changsha 410004,China)

The data from CAE simulation orthogonal test was used as training samples to establish the neural networks ensemble approximate calculation agent model.With clear mathematical formula,the model may carry out global optimization by genetic algorithm quickly and accurately,and the optimal processing parameters were obtained.By comparison and verification,this multiobjective optimization method could improve multiple quality indicators in the case of lacking sufficient orthogonal data.

injection molding;processing parameter;neural networks ensemble;multi-objective optimization;agent model;genetic algorithm

TQ320.66+2

B

1001-9278(2010)08-0064-08

2010-04-09

国家自然科学基金项目(10672191)

联系人,hzhaocs@sina.com