正方形截面气动外型优化仿真计算*

詹 昊 李万平 李龙安

(中铁大桥勘测设计院有限公司1) 武汉 430050)

(华中科技大学土木工程与力学学院2) 武汉 430074)

流体绕过钝体时,钝体表面边界层在逆压梯度下分离,在一定的雷诺数范围形成规则的旋涡结构,产生顺气流方向和垂直气流方向的作用力,易发生涡激振动,导致结构损伤或疲劳破坏.目前工程上主要采取机械措施(设置阻尼器)、空气动力学措施(改变结构气动外形)和来抑制涡激振动.机械措施所需成本及后期维护费用很高;气动力措施在保证结构安全的情况下改变结构气动外形,几乎无需增加成本及费用,因此气动截面选型显得十分重要.

对正方形截面的气动力性能已有大量的研究[1-2],但对于具有不同切角形状的正方形和长方形截面的气动力性能研究相对很少,可以参见H·Kawai,Tetsuro Tam ura,C·W·Park风洞试验结果[3-5].本文通过数值仿真计算研究了正方形截面、切角正方形截面、圆角正方形截面的气动力性能,并与文献值进行了比较.

1 边界层分离

边界层中的流体质点受惯性力、粘性力和压力的作用.其中粘性力阻滞流体运动,压力作用取决于绕流物体的形状,顺压梯度(d p/d x＜0)有助流体加速前进,而逆压梯度(d p/d x＞0)阻碍流体流动,边界层分离示意图如图1所示[6].

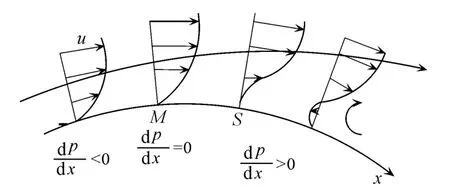
图1 边界层分离示意图(S为分离点)

在逆压梯度区,流体运动时,除克服粘性阻力外,还要克服压差阻力,故紧靠物面的流体质点的动能消耗很快,不断减速,在某位置处紧靠物面的流体质点速度降为零,前面的流体受逆压的作用出现倒流,形成具有回流的分离区.边界层分离后,从分离点不断脱出涡旋.在有逆压梯度的区域内,尤其是在压力曲线陡增的地方,边界层分离的可能性很大.当边界层的分离能推迟或完全消除,物体本身又具有低阻力外形时,可以有效地减小阻力.

2 仿真计算

2.1 控制方程

钝体绕流问题的控制方程是粘性不可压N-S方程,在直角坐标系下,基于雷诺平均的连续方程和动量方程分别为

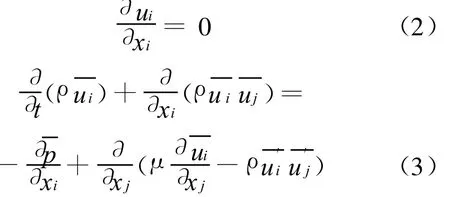
式中:μ为速度分量;p为压力;ρ为流体密度,空气密度常温时取1.225 kg/m3;μ为流体粘度,空气粘度常温时取1.8×10-5Pa·s.

2.2 湍流模型的选择

FLUENT提供的湍流模型包括:单方程(Spalart-A llmaras)模型、双方程模型(标准κ-ε模型、重整化群 κ-ε模型 、可实现(Realizable)κ-ε模型)及雷诺应力模型(RSM)等.仿真计算用RSM模型.RSM模型采用各向异性的湍动粘度计算湍流应力,比单方程和双方程模型更严格地考虑了旋转流动,流动方向表面曲率变化的影响,对复杂流动有更高精度预测潜力.

2.3 计算模型

计算模型截面,计算模型区域,计算模型网格分别如图2～4所示.

流体从左至右流动,左侧设定为速度入口,右侧设定为自由出流.入口速度v=9 m/s,雷诺数Re=30 000.上下边界为无滑移固壁边界.矩形计算区域为51D×21 D,模型上游来流区域为10 D,下游尾流区为40D,离上下边界各为10D.其中Re数定义为Re=UD/υ.式中:U为来流速度;D为钝体直径或迎风截面的特征尺度;υ为运动粘度,空气运动粘度取为常温下的1.5×10-5m2/s.

图2 计算模型截面图

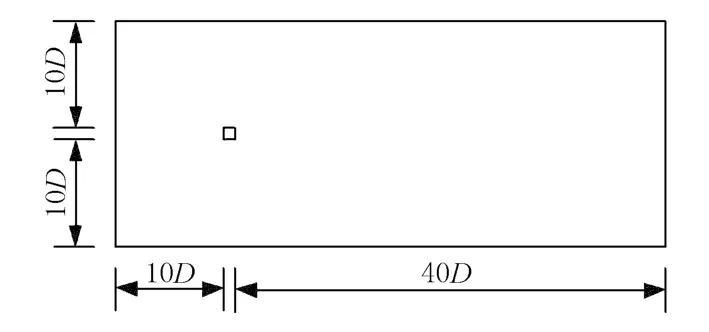
图3 计算模型区域图

图4 计算模型网格

3 仿真计算结果

3.1 物体表面压强分布图

物体表面压强分布如图5所示,各截面坐标如图6所示.

图5 物体表面压强分布图

图6 截面坐标

3.2 流线图和涡量图

各截面流线和涡量图如图7,图8所示.涡量定义为Ω=▽×u.式中:▽为哈密顿算子.对

图5中上面点对应物体上表面压强,下面点对应物体下表面压强.由图5可以看出,截面1在前侧压强变化急剧,压强值由60 Pa变化至-90 Pa,截面2在前面切角点处压强变化急剧,于截面1、截面2、截面3,流动分离点后移,尾流宽度变窄,涡距减小,涡脱落规模减小.

图7 流线图

图8 涡量图

3.3 气动力参数

各截面结构受力比较表,仿真计算结果与文献值比较表如表1和表2所列.

表1 各截面结构受力比较表

由表1可知,由截面1到截面3,结构单位长度所受到的平均阻力,最大升力幅值,平均俯仰力矩逐渐减小.表 2中 v=9 m/s,数Re=30 000,FLUENT仿真计算采用RSM 湍流模型,湍流强度仿真计算和风洞试验一样取14%.斯特劳哈尔数St定义为St=f s D/U.式中:f s是物体旋涡脱落频率.St数将边界层分离以及流动的不稳定性这些微观随机特性与表现相对稳定的泻涡频率联系起来,是计算涡激振动发振风速和最大振幅的重要参数.由截面1～截面3,St数逐渐增大,当结构自振频率相同时,它们涡激振动的发振风速将逐渐减小,通常结构的最大振幅也将逐渐减小.由表2可知,仿真计算值与文献值吻合良好.

表2 仿真计算结果与文献值比较表

4 结 论

1)优化正方形截面的角形状可以比较显著地改变截面的气动力性能.截面1～截面3,涡脱落规模减小,阻力、升力和俯仰力矩减小,其中截面3的气动力性能最好.

2)几何形状的微小变化会引起气动力系数值发生很大的变化,尤其在物体形状的变化强烈影响到压力分布的时候.当边界层的分离能推迟或完全消除,同时物体具有低阻力外形时,能有效地减小物体阻力.

3)在边界层不可避免发生分离的情况下,形(或压强)阻力一般决定了摩擦阻力,为了使形阻力最小,可以用改变表面曲率来推迟分离发生.

通过数值仿真分析可以较准确地计算出正方形及其不同切角截面的气动力参数,为工程结构气动截面选型提供重要依据.

[1]黄 娟,张志国.2D非稳态方柱绕流的数值模拟与分析[J].武汉理工大学学报:交通科学与工程版,2009,33(1):192-195.

[2]Lankadasu A,Vengadesan S.Onset of vortex shedding in p lanar shear flow past a square cy linder[J].International Journal of Heat and Fluid Flow,2008,29:1054-1059.

[3]Kaw aiH.Effect of cornermodifications on aeroelastic instabilities of tall buildings[J].Journal of Wind Engineering and Industrial Aerodynam ics,1998,74-76:719-729.

[4] Tamura T,M iyagi T.The effect of turbu lence on aerodynam ic forces on a square cylinder with various corner shapes[J].Journal of W ind Engineering and Industrial Aerodynam ics,1999,83:35-145.

[5]Park C W,Lee S J.Effect of free-end corner shape on flow struc ture around a finite cy linder[J].Joural o f Fluid and Structures,2004,19:,141-158.

[6]Schlichting H,Boundary-layer theory[M].7 th ed.Translated by Kestin J.New York:M cG raw-H ill Book Company,1979.