正交微切削中切削力预测模型研究*

吴继华 刘战强

(山东大学机械工程学院 济南 250061)

微切削作为微细产品的主要加工方式,具备加工材料范围广,成本低,加工精度高等特点,受到越来越多国家的高度重视,其加工机理受到广大研究者的关注.切削力研究可以用来监测刀具状态和预测刀具磨损,表征切削过程及计算流动应力等.对微切削切削力的深刻理解是研究微切削过程的基础.

应变梯度理论已成功的解释了微扭转、微压痕、复合材料增强实验中的尺度效应.Kai Liu用Abaqus软件仿真了铝A l5083-H 116的微切削过程,在定义材料时应用了泰勒非局部塑性理论,考虑了材料的应变梯度效应,认为考虑材料的应变梯度效应能更好地表示切削过程中的尺度效应[1].

因为微切削的切削用量在微米级,接近于材料的晶粒尺度,且不能忽略切削刃半径的影响,所以微切削的切削机理与宏观显著不同,表现在微切削过程中出现的尺度效应[2]、脆塑转换[3]、犁耕效应[4]等现象,宏观中的切削力模型不适用于微观.应变梯度理论的发展为此问题提供了很好的解决方案[5-8].本文基于应变梯度理论建立了正交微切削力的预测模型,并设计了正交微切削实验验证了微切削力模型的可靠性.通过分析实验数据阐明了微切削中切削力的变化规律.

1 微切削力预测模型

宏观中的二维切削力表示为[9]

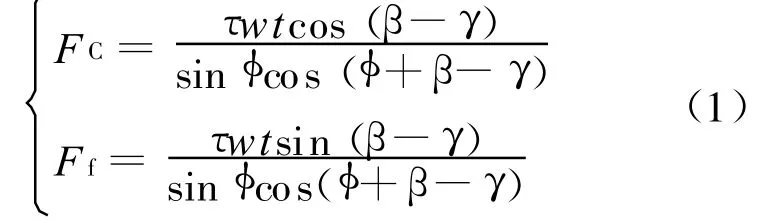
式中:FC为切削力;Ff为进给力;τ为平均剪切应力;w为切削宽度;t为切削厚度;φ为剪切角;β为摩擦角,γ为前角.

为了反应微切削过程中的尺度效应,用应变梯度理论计算平均剪切应力τ.基于位错理论的平均剪切应力为

式中:αc为塑性材料常系数,取 0.3～0.5;G为剪切模量;b为伯格斯矢量;ρtotal为总位错密度;ρSSD是统计存贮位错密度;ρGND为几何必需位错密度.

统计存贮位错发生在均匀的塑性变形过程中,几何必需位错则产生应变梯度,用几何必需位错密度ρGND表示应变梯度为

式中:η为应变梯度;L为剪切区长度.

式中:τ0为剪切屈服强度,可由材料的拉伸实验获得 ,则

将式(5)代入式(1),得

式(6)中剪切角φ由下式计算

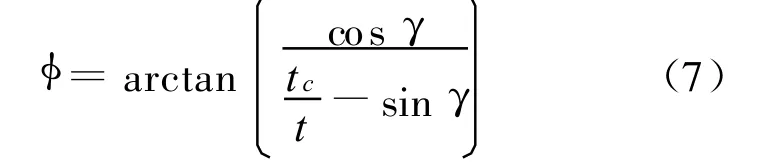
式中:tc为切屑厚度.

(1)微切削中实际起作用的前角称为实际前角γe.名义前角 γn为刀具的前刀面和基面的夹角,如图1.所以随进给量的变化,正交微切削中的前角定义为

式中:γe为切削刃口圆弧半径.

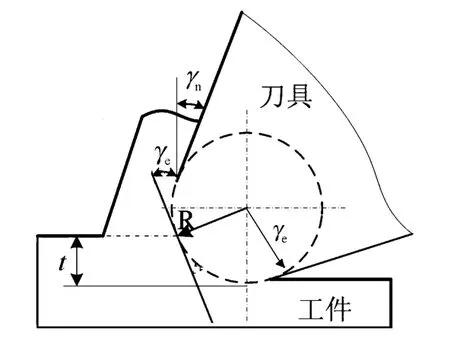
图1 微切削中前角的定义简图

(2)式(6)中摩擦角β的计算如下式

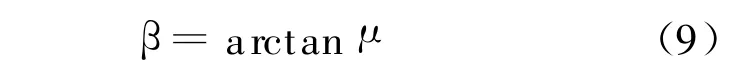
微切削中的摩擦因数 μ可以分为2部分:由于切削刃口犁切作用产生的粘着摩擦;由切削产生的滑动摩擦.μ=μp+μc.式中:μp为粘着摩擦因数;μc为滑动摩擦因数.

由Venkatachalam提出的犁切模型得到粘着摩擦因数为

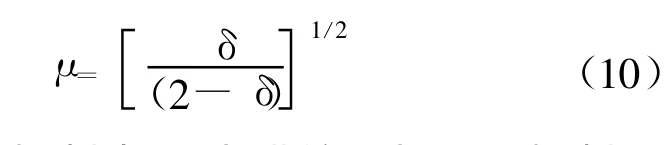
在正交微切削中,δ为进给量与刀具切削刃半径之比.

μc=k,k为常数,由刀具和工件材料确定.

2 正交切削实验

2.1 实验参数

1)实验目的 验证微切削力预测模型的可靠性.实验方案和工件几何形状如图2,实验参数如表1.

2)工件材料 45#钢,具有一定的塑性和韧性,切削性能良好.

3)刀具 Kenna KC9315 CNMG120408-UN,前角 0°、后角 10°、刃倾角 0°.

表1 微切削实验参数

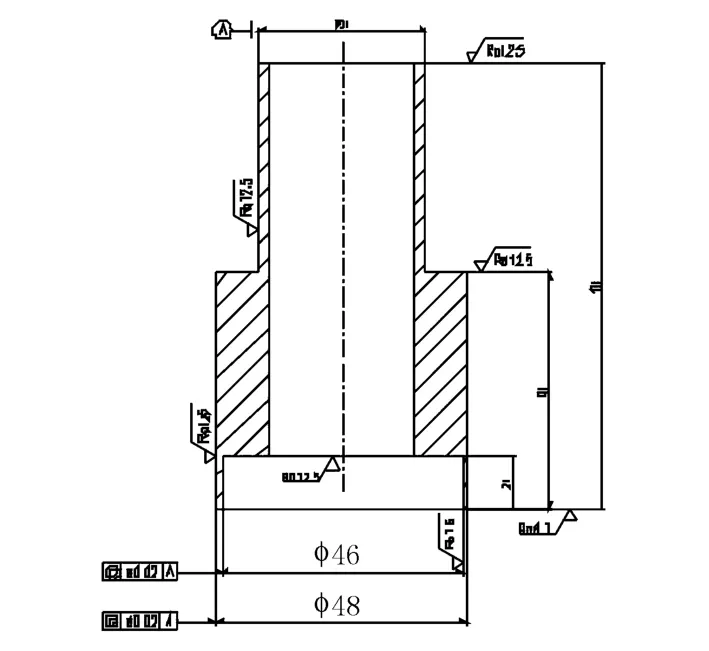
图2 工件几何尺寸(剖视)

实验采用瑞典生产的Kislter车削铣削测力仪测得正交微切削过程中的切削力,可以准确地获得水平分力F H(主切削力F c)和垂直分力F V(进给力Ff).连接方法如图3所示.

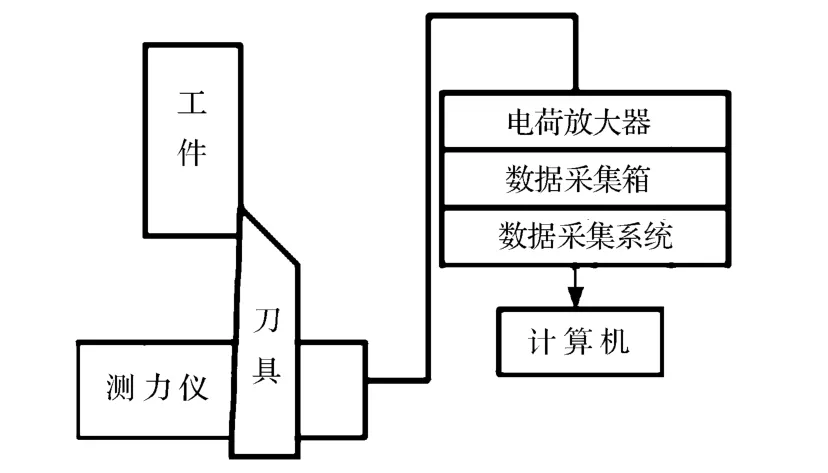
图3 测力仪连接示意图

2.2 实验数据分析

1)切削力随时间变化的关系 对实验获得的二维切削力进行分析.为了得到稳态切削过程中的切削力,选切削速度为5m/s时,切削过程开始0.8 s后的切削力数据.比较进给量为1μm/r和10μm/r时所得的切削力数据,切削力随时间变化的关系.如图4.

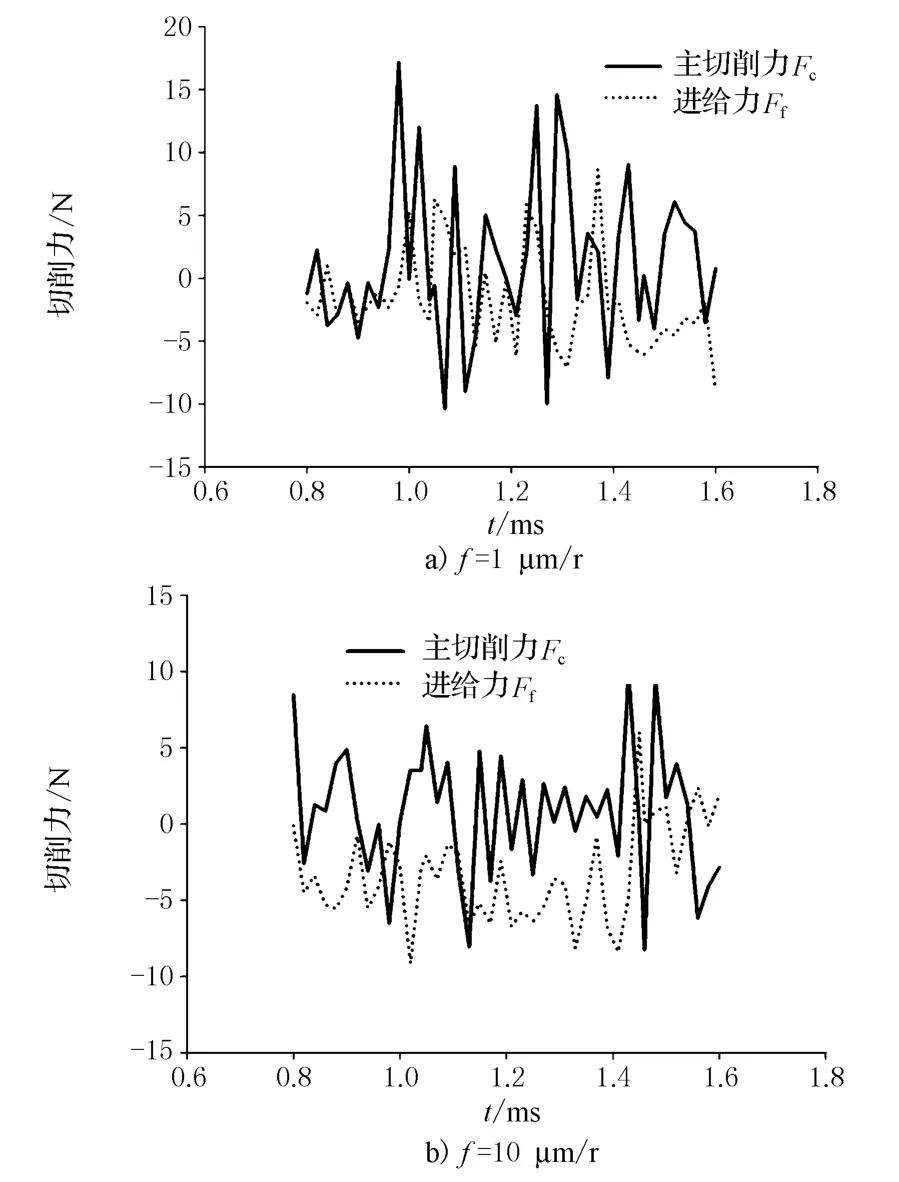
图4 V=5m/s切削力随时间变化

由图4可得,在正交微切削中主切削力在大多数时间内是大于进给力的.当在相同切削速度下,进给量越小,主切削力和进给力的变化程度越大.

2)切削力和进给量的关系 用进给量作为横坐标,主切削力和进给力的对数形式为纵坐标作图,分析切削力和进给量的关系,如图5.

图5 主切削力F c、进给力 F f与进给量的关系

由图5可得主切削力F c随进给量的增大而增大,而进给力F f随进给量的增大而减小.

用基于应变梯度的微切削模型计算切削力,取温度为200℃时,45#钢的剪切屈服强度τ0为340MPa,剪切模量G为 210GPa,伯格斯矢量b为0.304 nm,将所选择的加工参数代入式(6),计算获得切削力数据.

正交切削实验数据与预测模型数据进行比较,结果如表2.

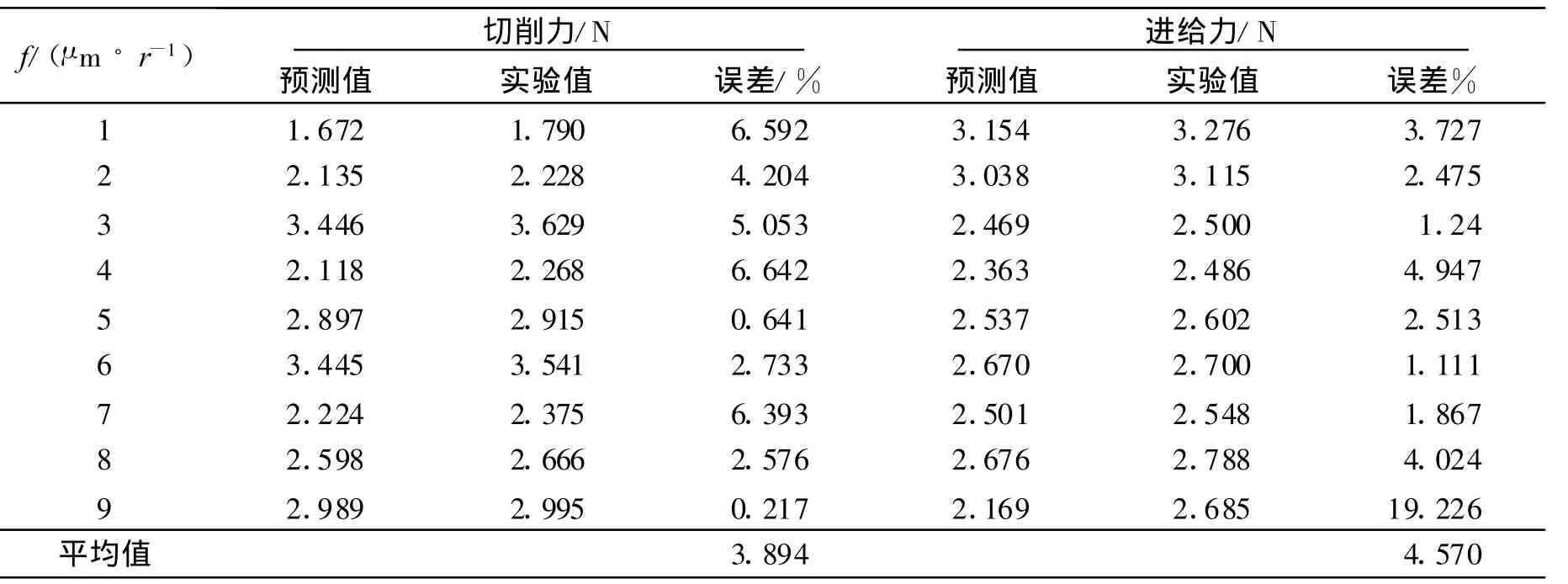
表2 切削力预测值和实验值误差

由表2可见应变梯度理论模型预测微切削中的切削力与实验数据相比,平均误差不超过5%,误差较小,说明在微切削中应用应变梯度理论预测切削力是合理的.

3 结 论

1)建立了基于应变梯度理论的切削力预测模型,应变梯度理论模型预测微切削中的切削力与实验数据相比,平均误差不超过5%.能更好的反映微尺度特征.说明在微切削中应用应变梯度理论预测切削力是合理的.

2)进行正交微切削实验,对45#钢在进给量范围为1～10μm内以不同的速度进行切削,测量切削力,分析切削力数据可得:在正交微切削中主切削力基本是大于进给力的;当在相同切削速度时,进给量越小时,主切削力和进给力的变化程度越大,原因是当进给量越小时,更接近晶粒的尺寸,切削过程中晶粒和晶界的破坏比晶粒间的滑移作用更居主要地位,使切削力产生较大变化;主切削力随进给量的增大而增大,而进给力随进给量的减小而增大.

[1]Kai Liu.Processesmodeling of m ic ro-cutting including strain gradienteffects[D].Georgia:Georgia Institute o f Techno logy,2005.

[2]盛 精,苑伟政,耿文轩.基于切削仿真的刀具一工件的参数化三维建模[J].武汉理工大学学报:交通科学与工程版,2007,29(1):65-69.

[3]Cai M B.Study of the mechanism o f nanoscale ductilemode cutting of silicon using molecular dynam ics simulation[J].International Journal o f Machine Tools&Manufacture,2007,47:75-80.

[4]Rosa P A R,Kolednik O,M artins P A F,etal.The transient beginning tomachining and the transition to steady-state cutting[J].International Journalof Machine Tools&Manu facture,2007,47:1904-1915.

[5]Dornfeld D,M in S,Takeuchi Y.Recent advances in mechanicalm icromachining[J].Annals of the ClRP,2006,55(2):745-768.

[6]K im J D,Kim D S.Theoretical analysis of m icrocutting characteristics in ultra-precision machining[J].Journal of M aterials Processing Technology,1995,49(3-4):387-398.

[7]Bao W Y,Tansel I N.Modeling m icro-end-m illing Operations.part I:analy tical cutting force model[J].International Journalof Machine Tools&Manu facture,2000,40(2000):2155-2173.

[8]Kang I S,Kim JS,Kim J H,et al.A mechanistic model o f cutting force in the m icro end m illing p rocess[J].Journa lo f M aterials Processing Technology,2007,187-188:250-255.

[9] Shaw M C.The size effect in metal cutting[J].Sadhana,2003,28:875-896.