相似初等变换及其应用
2010-11-27侯紫燕原新凤
侯紫燕,原新凤
(1.河南工程学院 数理科学系,河南 郑州 451191; 2.河南财经学院 成功学院,河南 巩义 451200)
相似是矩阵之间的一种基本关系,在一般的线性代数和高等代数教材中都可见到它的定义:设A、B为数域F上两个n阶方阵,如果存在F上的n阶可逆矩阵P,使B=P-1AP,则称B是A的相似矩阵,或称矩阵A与B相似.运算P-1AP称作对A进行相似变换,可逆矩阵P称作把A变为B的相似变换矩阵.
显然,已知A与P按定义立即可得到B.但相反的问题是,如果已知n阶方阵A与B相似,那么相应的相似变换矩阵P如何来求得.在常见的教材中,仅就B为对角矩阵时,讨论了通过求A的特征值、特征向量来获得P的方法,但当B中的元素排列形式较为复杂一些时,如根据初等因子和不变因子理论,在复数域上方阵A必与它的若当标准型J相似,在任意数域F上方阵A必与它的有理标准型B相似.教材中一般依据论证结果直接给出J与B的求法,而跳过了求相似变换矩阵P的过程,这往往使得初学者对连接两个相似矩阵的桥梁——相似变换矩阵P产生了莫大的悬念.因此,有必要提供一种求P的方法,以消除初学者的疑虑,还可充分利用求P的过程,提炼出其他相关的概念,帮助学生将各知识点融会贯通、深刻理解、学以致用.
本文将从矩阵相似定义出发,分析利用矩阵相似初等变换求相似变换矩阵P的原理,并通过实例展示求P的具体过程,最后借助求P的过程和矩阵相似的性质,提炼出不用求解特征方程而获得方阵全部特征值、与不用求解线性方程组而获得方阵全部线性无关特征向量的方法.
1 基本原理与基本运算步骤
1.1 基本原理
矩阵的初等变换是贯穿于线性代数、高等代数教材的一个重要工具,而矩阵的初等变换与矩阵的乘法又有着密切的联系.
引理1[1]对一个s×n矩阵A作初等行变换,就相当于在A的左边乘上相应的s×s初等矩阵;对A作初等列变换,就相当于在A的右边乘上相应的n×n初等矩阵.
引理2[1]n级矩阵A为可逆的充分必要条件是它能表示成一些初等矩阵的乘积.
因此,若A、B两个n阶方阵相似,则存在n阶可逆方阵P使B=P-1AP,也即意味着存在一些初等矩阵P1,P2,…,Pi,使P=P1P2…Pi.初等矩阵都是可逆矩阵,且它们的逆矩阵还是初等矩阵,于是有:
B=(P1P2…Pi)-1A(P1P2…Pi)=
其中,P(i,j)-1=P(i,j),P(i(k))-1=
P(i(k-1)),k≠0,P(i,j(k))-1=P(i,j(-k)).
其中,Q(i,j)-1=Q(i,j),Q(i(k))-1=Q(i(k-1)),k≠0,Q(i,j(k))-1=Q(i,j(-k)).
于是,由A到B所做的相似变换运算P-1AP相当于对A成对地做一系列初等行变换与初等列变换.不妨称每做一对初等行变换与初等列变换为一次相似初等变换.
1.2 基本运算步骤
定义(相似初等变换)
(1) 先交换A的i,j两行得A1,再对A1交换i,j两列得B1.
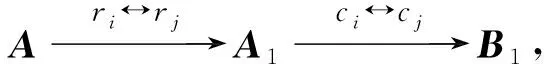
(2) 先用非0常数k乘A的第i行得A2,再用非0常数k-1乘A2的第i列得B2.
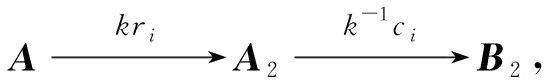
(3) 先用常数k乘A的第j行,且把乘得的结果加到A的第i行上去得A3,再用-k乘A3的第i列,且把乘得的结果加到A3的第j列上去得B3.
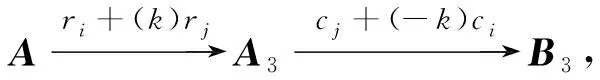
结论1 每一次相似初等变换都把一个n阶矩阵A变换为与其相似的另一个同阶矩阵B.
结论2 用n阶方阵A和n阶单位阵In以及n阶零阵On构造2n×2n阶分块矩阵,对其中的A施加相似初等变换,使之变换为B,则B相似与A,与此同时左下角的n阶单位阵In则变换成为相似变换矩阵P,而右上角的n阶单位阵相应地变换成为P-1.

2 实例分析
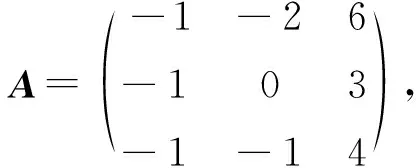
2.1 求A的若当标准型J

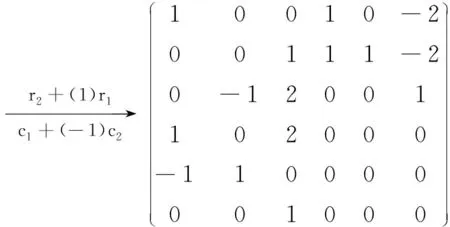
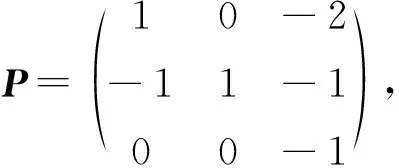
2.2 求A的有理标准型B


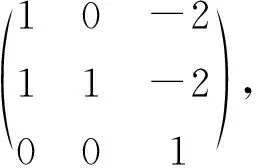
2.3 两点说明
2.3.1 相似变换矩阵P不唯一
求A的有理标准型还可以通过下面的变换过程得到:

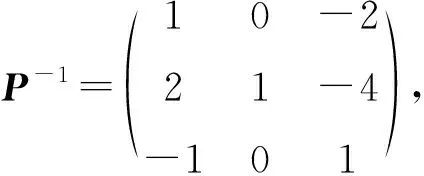
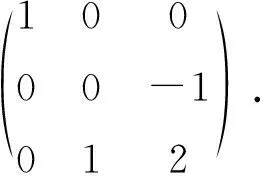
2.3.2 做第三类相似初等变换时选常数k的方法
在使用第三类相似变换时,其中k的选取应该满足下列关系:
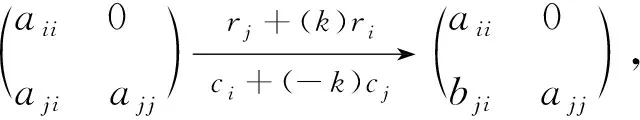
3 用相似初等变换求矩阵特征值和特征向量
3.1 求特征值
引理3[1]相似的矩阵有相同的特征多项式.
根据引理3,若方阵A与C相似,则他们有相同的特征值,又由于上(下)三角矩阵的特征值即其主对角线上的元素.
结论3 求n阶方阵A的特征值,可先通过相似初等变换将A变换为一个上(下)三角矩阵,则该三角矩阵的主对角元素即为A的全部特征值.
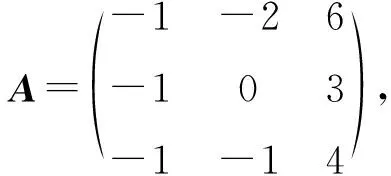
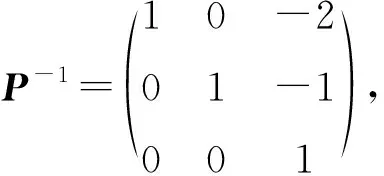
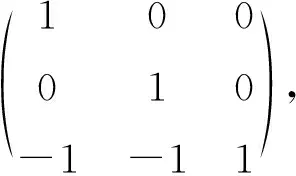
3.2 求特征向量
注意到n阶方阵A的若当标准型矩阵J是上(或下)三角矩阵,于是J的主对角线上的n个元素即A的全部n个特征值,再注意到把A变换成J的相似变换矩阵P是可逆的,即P的列向量组是一线性无关向量组.据此,我们再以3阶方阵A为例,不经过求解线性方程组而找出A的全部线性无关的特征向量.
由2中计算结果,对于3阶方阵A=
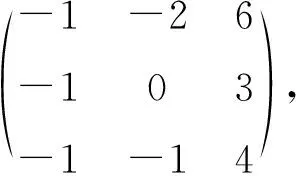
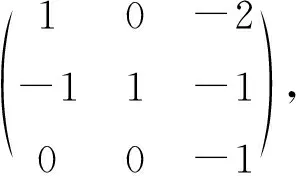
令P=(P1,P2,P3),
则有A(P1,P2,P3)=(P1,P2,P3)

4 结 论
初等变换是代数研究过程中的一个重要工具,相似是矩阵间的一种基本关系,求矩阵的特征值特征向量是线性代数的一项基本要求.本文尝试在讲清楚各自基本概念与基本方法的基础上,恰当调动概念之间的联系,给出了求得初等变换阵的一种一般的方法,有助于在线性代数学习中打通知识点之间的关系,得到对初等相似变换的深刻理解.
参考文献:
[1] 北京大学数学系. 高等数学[M].3版.北京:高等教育出版社,1988.
[2] 赵树嫄. 线性代数[M].4版.北京:中国人民大学出版社,2008.
