B2型的基及其基变换
2010-12-28郝晓斌原新凤
郝晓斌,原新凤
(河南工程学院数理科学系,河南郑州 451191)
B2型的基及其基变换
郝晓斌,原新凤
(河南工程学院数理科学系,河南郑州 451191)
令v是未定元,A=Z[v,v-1],A=Q(v)是A的分式域.UA′是A′上相伴于B2型 Cartan矩阵(aij)的量子代数.分析了UA′的子代数U+A′的两组包含无限个元素的典范基的结构,对于一组基中任一元素,都可以在这组基中找到一个包含该元素的有限集合,同时在另一组基中可以找到一个对应的有限集合,这两个集合元素个数相等,两者元素可互相表出.
量子代数;子代数;基变换
量子群作为经典李群、李代数的基本对称概念的推广,有着丰富的代数、几何及物理性质.近二十年来,量子群理论引起了许多数学家和数学物理学家的注意,目前这一理论已取得了很大的发展.例如,Lambe和 Radford等系统地研究了量子群和一般 Hopf代数与量子 Yang-Baxter方程的解的关系[1];Luszting、Rosso和 Anderson等研究了任意有限维半单李代数g的量子包络代数Uq(g)的表示[2-6].文献[7]给出了A′上B2型量子代数的两组典范基.本文进一步分析这两组基的结构,给出了它们之间基变换.



以上两组基都有无限个元素.本文的结论是在一组基中任取一元素,都可以在这组基中找到一个包含该元素的有限集合,对应地在另一组基中找到另一个有限集合,这两个有限集元素个数相等,两者元素可互相表出.
1 B2型量子代 的子代数 典范基


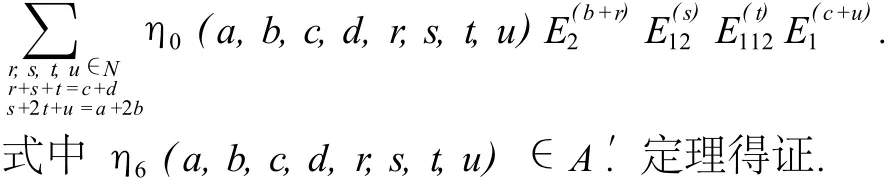
2 B2型量子代数 子代数 基变换


[1]LAMBE L A,RADFORD D E.Algebraic aspects of the quantum Yang-Baxter equation[J].J.Algebra,1993(154):228-288.
[2]ANDERSEN H H,POLP P,WEN K X.Representations of quantum algebras[J].Invent Math,1991(104):1-59.
[3]LUST ING G.Finite d imensional hopf algebras from quantized universal enveloping algebras[J].Amer.Math Soc,1990(3):257-296.
[4]LUST ING G.Canonical bases arising from quantized enveloping algebras[J].Amer.Math Soc,1990(3):447-498.
[5]LUST ING G.Modular representations and quantum groups[J].Contemp.Math,1989(82):59-77.
[6]LUST ING G.Quantum groups at roots 1[J].Geom.Dedicata,1990(35):89-113.
[7]XINanhua.Canonical basis for type B2[J].Journal of Algebra,1999(214):8-21.
Basis and Their Transformation offor TypeB2
HAO Xiaobin,YUAN Xinfeng
(Departm ent of M athem atical and Physical Sciences,Henan Institute of Engineering,Zhengzhou451191,China)
Letvbe an indeterminate,A=Z[v,v-1],A=Q(v)is the fraction field ofis the quantum algebra overA′associated to Cartan matrix(aij)for typeB2.The constructions of two infinite canonical bases of the subalgebraofare discussed.For any element in one basis,there is a finite setwhich includes this element.At the same time,a corresponding finite set can be found in another basis,the two sets above-mentioned have the same cardinality and can be expressed each other.
quantum algebra;subalgebra;the transfo rmation of basis
O153
A
1674-330X(2010)03-0065-03
2010-07-01
河南工程学院博士基金项目(D09008)
郝晓斌 (1974-),男,河南平顶山人,讲师,博士,主要从事数学教学和有限元方法、量子群研究.
