关于限制广义逆的通式

2010-11-27何楚宁

湖南师范大学自然科学学报 2010年1期

何楚宁

(湖南师范大学数学与计算机科学学院，中国长沙 410081)

给定A∈Cm×n,下列矩阵方程：

(1)AGA=A，(2)GAG=G，(3)(AG)*=AG，(4)(GA)*=GA

称为penrose方程.如果G满足上述方程(i),(j),…(k),则称G为A的(i,j,…,k)逆或penrose型广义型，简称广义逆，并记为A(ij…k).其全体记为A{i,j,…,k}.{1234}逆常记为A+，叫做Mooer-penrose逆.广义逆矩阵的理论在数学的许多分支及应用科学中发挥了广泛的重要作用[1-6]；penrose型广义逆有15类，其中除A+外，其余均不唯一.研究广义逆的各种表示或通式，一直是广义逆研究的重要课题之一[1-15].本文将研究在某种限制条件下的广义逆通式问题，其具体内容是：

设E∈Cp×n,F∈Cp×m.S={X∈Cn×m|EX=F}.令A{i,j,…,E,F}=A{i,j,…,k}∩S,A{i,j,…,E,F}中元素记为A(ij…EF),叫做A的满足限制条件S的广义逆，简称限制广义逆.本文首先讨论5类限制广义逆A{1，E，F}，A{3，E，F}，A{4，E，F}，A{1，3，E，F}及A{1，4，E，F}存在的充分必要条件以及它们的通式，然后给出了限制广义逆A{1,2,E,F}存在的两个充分条件及其通式.因为本文所给出的这些通式，是在未借助矩阵的任何分解的前提下得到的，因此，它们将在宏观上研究矩阵方程的理论和应用问题方面发挥重要作用.

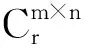
引理1[1-4]设A∈Cm×n,B∈Cp×q,F∈Cm×q,则矩阵方程AXB=F有解X∈Cn×p的充要条件是AA-FB-B=F；当方程有解时，其通解为：X=A-FB-+U-A-AUBB-，其中U∈Cn×m.

引理2[1-4]设G∈A{1,3},则G=A(13)+(I-A-A)U,U∈Cn×m.特别地，A{1，3}的通式亦为G=A++(I-A+A)U，U∈Cn×m.

推论1对任意G1,G2∈A{1,3},有AG1=AG2.

引理3[1-2]设G∈A{1,4},则G=A(14)+U(I-AA-),U∈Cn×m.特别地，A{1，4}的通式亦为G=A++U(I-AA+)，U∈Cn×m.

推论2对任意G1,G2∈A{1,4},有G1A=G2A.

引理4A{3}的通式为G=A+AgA++(I-A+A)U,g∈Hm,U∈Cn×m.

证将文[15]定理1(3)式中的A-取为A+，y取为(I-A+A)U，g取为-g即得本引理的结论.

引理5A{4}的通式为G=A+gAA++U(I-AA+),g∈Hm,U∈Cn×m.

证将文[15]定理1(4)式中的A-取为A+，z取为U(I-AA+)，g取为-g即得本引理的结论.

主要结果

定理1A{1，E，F}非空的充要条件是

1)EE-F=F；2)A(I-E-E)(A(I-E-E))-(I-AE-F)A=(I-AE-F)A.

并且在条件成立时，A{1，E，F}有一个元素

x*=E+F+(I-E+E)P+(I-AE+F)AA+.

(1)

其元素的通式为

G=x0+(I-E-E)(y-P-PyAA-),

(2)

其中y∈Cn×m,P=A(1-E-E),x0是A{1,E,F}的某个固定的元素.

证设A{1，E，F}非空.即矩阵方程AxA=A与Ex=F有公共解G，由引理1，条件1)成立，并且G可表为

G=E-F+(I-E-E)U,

(3)

其中U∈Cn×m.令P=A(I-E-E)，将(3)式代入penrose方程(1)，整理得

PUA=A-AE-FA.

(4)

因(4)式有解，则由引理1，条件2)成立，必要性得证.并且从(4)解出U=P-(I-AE-F)AA-+y-P-PyAA-,代入(3)整理得

G=E-F+(I-E-E)P-(I-AE-F)AA-+(I-E-E)(y-P-PyAA-).

(5)

(5)式中令x0=E-F+(I-E-E)P-(I-AE-F)AA-得(2)式，可以验证x0∈A{1,E,F}.反之，当条件1)，2)成立时，直接可以推得(1)式中x*∈A{1,E,F}.故充分性得证.注意到，对任意G0∈A{1,E,F},E(G0-x0)=0,P(G0-x0)A=A(G0-x0)A-AE-E(G0-x0)A=0,因此G0可表为(2)中取y=G0-x0的形式，从而(2)是A{1，E，F}通式.定理得证.

定理2A{1，3，E，F}非空的充要条件是对某个A-和A(13)，有

1)EE-F=F;3)E(I-A-A)(E(I-A-A))-(F-EA(13))=(F-EA(13)).

并且条件成立时，A{1，3，E，F}有一个元素

x*=A++(I-A+A)Q+(F-EA+).

(6)

其元素的通式为

G=x0+(I-A(13)A)(I-Q-Q)y,

(7)

其中y∈Cn×m,x0是A{1，3，E，F}的某个固定的元素，Q=E(I-A-A).

证设A{1，3，E，F}非空，即矩阵方程AxA=A,(Ax)*=Ax与Ex=F有公共解G，由引理2，G=A(13)+(I-A-A)U，并且

E(I-A-A)U=F-EA(13).

(8)

因(8)式有解，则由引理1，条件3)成立，必要性得证.令Q=E(I-A-A)，从(8)式中解出U=Q-(F-EA(13))+(I-Q-Q)y,

G=A(13)+(I-A-A)Q-(F-EA(13))+(I-A-A)(I-Q-Q)y.

(9)

(9)式中令x0=A(13)+(I-A-A)Q-(F-EA(13))得(7)式.当条件1)，2)成立时，容易验证x0∈A{1,3,E,F},而(6)中x*是x0的特殊情况，故x*是A{1，3，E，F}的一个元素，故充分性得证.又对任意G0∈A{1,3,E,F},由E(G0-x0)=0和推论1，能推得G0可以表为(7)式取y=G0-x0的形式，从而(7)是A{1，3，E，F}通式.定理得证.

定理3A{1，4，E，F}非空的充要条件是对某个A(14)，有

1)EE-F=F;4)EE-(F-EA(14))(I-AA(14))=(F-EA(14)).

并且条件成立时，A{1，4，E，F}有形如

G=A(14)+E-(F-EA(14))(I-AA(14))

的元素，特别有一个元素

x*=A++E+(F-EA+)(I-AA+).

(10)

并且A{1，4，E，F}元素的通式为

G=x0+(I-E-E)y(I-AA(14)),

(11)

其中y∈Cn×m,x0是A{1，4，E，F}的某个固定的元素.

证必要性的证明过程与定理3的类似.充分性是因为当条件1)，4)成立时，直接可以验证(10)中x*∈A{1,4,E,F}.最后，利用推论2可得，对任意G0∈A{1,4,E,F},G0可表为(11)中取y=G0-x0的形式，从而(11)是A{1，4，E，F}通式.定理得证.

定理4令Q=E(I-A+A)，则A{3，E，F}非空的充要条件是

1)EE-F=F;5)存在g0∈Hm,使得QQ-(F-EA+g0AA+)=F-EA+g0AA+.

并且条件成立时，A{3，E，F}有一个元素

x*=A+g0AA++(I-A+A)Q-(F-EA+g0AA+).

(12)

其元素的通式为

G=x0+(I-A+A)(I-Q-Q)y，

(13)

其中y∈Cn×m,x0是A{3，E，F}的某个固定的元素.

证设A{3，E，F}非空，根据引理4，存在G0=A+g0AA++(I-A+A)U0,g0∈Hm,U0∈Cn×m,使得EG0=F,即有QU0=F-EA+g0AA+，由引理1，得条件5). 反之，当条件1)，5)成立时，容易验证(12)式中的x*∈A{3,E,F},(13)式中的G∈A{3,E,F},并且，对任意G0∈A{3,E,F},G0可表为(13)式中y取G0-x0的形式.证毕.

推论3对任意g∈Hm,令Gg=A+gAA++(I-A+A)Q-(F-EA+AA+),则当条件EE-F=F和Q-QE=E成立时，有Gg∈A{3,E,F}.

证因为由EE-F=F和Q-QE=E可推出Q-QF=F，所以对任意g∈Hm,有QQ-(F-EA+gAA+)=F-EA+gAA+,由定理4，结论成立.证毕.

定理5A{4，E，F}非空的充要条件是

1)EE-F=F；6)存在g0∈Hm,使得FAA+=EA+Ag0A+.

并且条件成立时，A{4，E，F}有一个元素x*=A+Ag0A++E-F(I-AA+).其元素的通式为

G=x0+(I-E-E)y(I-AA+),

其中y∈Cn×m,x0是A{4，E，F}的某个固定元素.

证若有G0∈A{4,E,F},由引理5，则存在g0∈Hm,U0∈Cn×m,G0=A+g0AA++U0(I-AA+),满足EG0=EA+g0AA++EU0(I-AA+)=F,于是EE-(F-EA+g0AA+)(I-AA+)=F-EA+g0AA+,即EE-F(I-AA+)=F-EA+g0AA+，从而FAA+=EA+Ag0A+.必要性得证.后续证明与定理4的证明类似.

下面给出关于A{1，2，E，F}的解存在的两个充分条件.

定理6令Q=E(I-A+A)，则当条件EE-F=F和QQ-(FAA+-EA+)=F-EA+成立时，A{1，2，E，F}有解x*=A++(I-A+A)Q-(FAA+-EA+).

证略.

定理7令Q=E(I-A+A)，P=I-AA+.则当EE-F=F并且条件

7)QQ-(FAA+-EA+)=F-EA+；8)F∈(R(I-AA+))⊥

成立时，A{1，2，E，F}的通式为

G=A++A+WP+(I-A+A)Q-(FAA+-EA+)(I+WP)+(I-A+A)(I-Q-Q)UA+(I+WP),

(14)

其中U∈Cn×n,W∈Cm×m.

证设G由(14)式给出，不难验证则GAG=G，AGA=A；又利用条件7)，可推得EG=F+FW(I-AA+)，再利用条件8)知FW(I-AA+)=F((I-AA+)W*)*=0,所以EG=F，于是G∈A{1,2,E,F}.反之，对任意G0∈A{1,2,E,F},经过推导可知，G0能表为(14)式右边取W=AG0，U=G0A的形式，故(14)是A{1，2，E，F}的通式.

参考文献：

[1] BEN-ISRAEL A, GREVILLE I N E.Generalized inverses, theory and applications[M]. 2nd Edition.New York:Springer Verlag, 2003.

[2] WANG G, WEI Y, QIAO S. Generalized inverses, theory and comput[M].Beijing:Science Press,2004.

[3] 王国荣.矩阵与算子广义逆[M].北京：科学出版社，1998.

[4] 何旭初，孙文瑜.广义逆矩阵引论[M].南京：江苏科学技术出版社，1990.

[5] RAO C R, MITRA S K. Generalized inverses of matrices and its applications[M]. New York:Wiley, 1971.

[6] WEI Y M. A characterization and representation of the generalized inverse and its application[J]. Linear Agebra Appl, 1998,280:87-96.

[8]MIAOJM.RepresentionsforweighedMoore-Penroseinverseofapartitionedmatrix[J].JCM, 1989,(7):320-323.

[9] 孙文瑜.关于广义逆的通式[J].南京大学学报：自然科学版，1984,(3):441-446.

[10] 庄瓦金.任意体上矩阵P. Moore-Penrose逆的某些显公式[J].数学季刊，1988，(3)：1-6.

[11] 庄瓦金.四元数矩阵的加正定权的Moore-Penrose型广义逆的显公式[J].数学的认识与实践，1988，(3)：68-74.

[12] 何楚宁.复矩阵的几种Penrose逆的通式[J].曲阜师范大学学报：自然科学版，1996，(1)：17-20.