粒子群算法在油田管网优化中的应用

蔡昌新

(长江大学电子信息学院，湖北 荆州 434023)

粒子群算法在油田管网优化中的应用

蔡昌新

(长江大学电子信息学院，湖北 荆州 434023)

在油田地面工程设计中，地面管网布局占有很大比重。为了优化布局和节约投资，结合邻近粒子群算法给出了油田地面管网布局数学模型，根据模型特点，采用改进邻近粒子信息的粒子群算法进行求解。为了有效地平衡算法在管网布局的全局探索和局部寻优，采用了时变加速因子策略。实例计算表明，改进的邻近粒子信息的粒子群算法优于遗传优化方法。

粒子群算法；油田管网；优化

在油田地面管网布局中，包括了注水管网和油气集输管网这两部分的设计，在设计过程中会涉及到很多的站及管网的合理分布问题，为了考虑投资成本，许多科学研究人员利用了各种优化方法，对生产过程中站和管网的模型进行了研究，并以油田集输及配水站之间的站点数最少和管网路径最短为最优结果。但是往往在求解过程中，由于具有高度的非线性和多维多参量的合理分布问题，所应用的相关优化方法针对实际问题很难满足要求，并且在求解过程中易陷入局部最优，效果较差。

粒子群优化(PSO)算法是一种新的基于群体智能的优化算法，是在鸟群觅食行为规律的基础上提出的[1,2]。同遗传算法相比较，不但具有遗传算法的全局寻优能力，而且通过调整相关参数还可以同时具有较强的局部寻优能力。由于没有个体杂交、变异等操作，其参数调整简单易行，更适合计算机编程处理，在多数情况下，比遗传算法更快地收敛于最优解。笔者在标准PSO算法的基础上引进了带邻近粒子信息的加速因子策略，根据种群的多样性测度来调整惯性权重，由此平衡算法的全局探索和局部开发能力，并将PSO算法应用于管网及站点分布的寻优中，取得了较好的效果。

1 数学模型

PSO算法是由Kennedy和Eberhart在1995年提出，是一种模拟鸟群飞行觅食的行为，通过个体之间的协作来寻找最优解的进化计算技术[1，2]。在油田管网和站点的布局更像一种粒子群，在该群中寻求最优路径更像鸟群觅食一样，因此利用粒子群算法通过反复迭代寻求最优路径更加简单和有效。假设从一个站点开始搜索，其搜索空间为N维，粒子总数为n，即对应站点数n，第i个粒子在N维空间的位置表示为xi，飞行速度表示为vi，即最优路径vi。每个粒子都具有一个由被优化的目标函数决定的适应值，并且知道自己到目前为止所发现的最好位置pi和现在的位置xi，每个粒子都知道目前为止整个群体所发现的最好位置pg。每个粒子的位置按式(1)、式(2)进行变化。

(1)

(2)

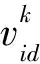
w=wmax-(wmax-wmin)×k/G

(3)

式中，wmax、wmin分别是w的最大和最小值；G,k分别为最大迭代次数和当前迭代次数。

标准PSO算法在进化过程中除跟踪自身最优外，只与种群最优粒子发生信息交流，在进化过程中种群最优对其影响很大，一旦粒子赶上种群最优，粒子会聚集到相同位置并停止，从而导致算法过早收敛而出现早熟。为了降低种群最优粒子的影响，笔者在粒子位置更新时除考虑自身最优和种群最优外，还与粒子目前位置最近粒子最优发生信息交流。粒子速度按式(4)进行变化：

(4)

式中，c3为权重因子；pid为与粒子i目前位置最近粒子的历代最好位置pi的第d维分量，即为站点与集输站之间的最优路径。

在PSO算法中，粒子位置更新由3部分组成，第1部分为粒子先前的速度；第2部分为“认知部分”，是粒子对自身的思考；第3部分为“社会部分”，表示粒子间的信息共享和相互合作。从式(4)中可以看出，社会部分包括了与种群最优粒子和目前位置最近粒子最优之间的信息交流。一般在群体智能搜索优化中，在初期应保持较高的多样性，应减小种群最优的影响，而增加最近粒子的影响，防止粒子向种群最优位置聚集，因此c2应取相对较小值，c3应取相对较大值；在进化后期，为了使算法收敛到全局最优，应加强全种群最优粒子的影响，而减小最近粒子的影响，因此c2应取相对较大值，c3应取相对较小值。由此，采用随进化代数线性变化改变c2和c3的值，其变化形式为：

c2=c2i+(c2h-c2l)×k/iter

(5)

c3=c3h-(c3h-c3l)×k/iter

(6)

式中，iter为最大进化代数；c2h,c2l为c2变化的上界和下界；c3h,c3l为c3变化的上界和下界。本研究中c3h,c2h都取为1.5，而c3l,c2l都取为0.5。

2 算法的实现

综上所述，算法的流程描述如下：

1)初始化粒子群，包括各参数，粒子的速度位置和个体极值pbesti，全局极值pbestl；

2)按式(2)和式(3)更新粒子的速度和位置；

3)计算种群中各个粒子的适应度，根据适应度更新粒子的个体极值pbesti和全局极值pbesil；

4)判断是否满足局部模型终止条件，如满足转5)，否则转2)；

5)初始化粒子的全局极值pbestl；

6)按式(1)和式(2)来更新粒子的速度和位置；

7)计算种群中各个粒子的适应度，根据适应度更新粒子的个体极值pbesti和全局极值pbesil；

8判断是否满足终止条件，如不满足则转6)，否则停止计算；

9)结束。

3 算法性能测试

为了测试笔者所提的算法(MPSO)的有效性，应用MPSO对2个经典的函数优化进行仿真，并与文献[4]所提出的带压缩因子的粒子群算法(CFPSO)[6]进行比较。2个测试函数为：

Rosenbrock函数：

Rastrigrin函数：

2个优化函数的搜索区间、目标值见表1。

表1 测试函数的维数、初值范围和目标值

f1是一个非凸的病态函数，在xi=1时达到极小值。f2是一个多峰函数，当xi=0时达到全局极小点，在其周围存在多个局部极小点。各种算法种群数取为20，wmax=0.95，wmin=0.4，在MPSO算法中c1=2.0，c2随进化代数从0.5增大到1.5，c3随进化代数从1.5下降到0.5，最大进化代数都为2000，2种算法对2个函数独立运行20次，其计算结果见表2。

表2 MPSO和CFPSO算法计算结果

表2的结果显示MPSO算法无论在平均最优值还是在标准方差上都比CFPSO要优。最小最优值时的进化曲线如图1所示。从图1中可以看出在进化早期，MPSO的适应度值和CFPSO的适应度值相差不大，而在进化的中后期MPSO的适应度值比CFPSO的适应度值小很多。其主要原因是MPSO在进化过程中加强了全局探索和局部优化的平衡，在进化早期增强了种群多样性，进化后期加强局部开发，从而使得算法更易收敛到最优值。

图1 进化过程中平均适应度变化曲线

4 应用实例

以江汉油田某实验区为例，该区设计注水井54口，配水间7座，注水站l座。为了便于比较，分别使用遗传算法、CFPSO和MPSO进行求解。传统遗传算法平均运行结果为69.58km，而CFPSO、 MPSO算法的平均运行结果分别为69.52km、66.23km。在该例中，采用MPSO算法比其他2种优化方法得到的结果要好。

5 结 语

笔者在标准PSO算法中粒子位置更新的基础上，引入了与目前位置最近粒子之间的信息交流。在分析算法进化过程中探索能力和局部开发能力的基础上，采用了带邻近粒子信息的MPSO算法进行管网优化方面的尝试，得到了比较满意的结果。

[1]Kennedy J，Eberhart R. Particle swarm optimization[A].IEEE Int Conf Neural Networks[C].1995.1942～1948.

[2]Shi Y, Eberhart R. A modified particle swarm optimizer[A].EEE World Congress on Computational Intelligence[C].1998.69～73.

[3] Zhang Liping, Yu Huanjun, Hu Shangxu. A new approach to improve particle swarm optimization[A]. Lecture Notes in Computer Science[C].Chicago,IL:Springer-Verlag,2003.134～139.

[4] Shi Y, Eberhart R C. Fuzzy Adaptive Particle Swarm Optimization[A]. Proceedings of the IEEE Conference on Evolutionary Computation[C]. Piscataway, NJ: IEEE Press, 2001.101～106.

[5] 刘扬, 魏立新. 油气集输系统拓补布局优化的混合遗传算法[J].油气储运,2003,22(6):33～36.

[6] Clerc M. The swarm and queen: towards a deterministic and adaptive particle swarm optimization[A]. Proceedings of IEEE Congress on Evolutionary Computation[C].Washington D C，1999.1951～1957.

[7] Qi Xiaofeng. Theory analysis of evolution algorilthms with an infinite population size in continuous space, part 2: analysis of the diversification role of crossover[J]. TEEE Trans Neural Network, 1994,5(1):120～129.

[8] Srinivas M.Adaptive probability of crossover and mutation in genetic algorithms[J]. IEEE Trans Syst Man Cybern, 1994, 24(4):655～ 667.

[编辑] 易国华

TP391.9

A

1673-1409(2010)03-N080-03

2010-06-22

蔡昌新(1974-)，男，1998年大学毕业，讲师，博士生，现主要从事油气田装备与智能控制等方面的研究工作。