具有切换拓扑和时滞的复杂网络自适应同步控制研究

周武能 王天波 钟庆昌 方建安

(东华大学信息科学与技术学院，上海 201620 中国科学院上海微系统与技术研究所无线传感器网络与通信重点实验室，上海 200050) (东华大学信息科学与技术学院，上海 201620；上海工程技术大学基础教学学院，上海 200051) (拉夫堡大学航空与汽车工程学院，莱斯特 英国 LE11 3TU) (东华大学信息科学与技术学院，上海 201620)

具有切换拓扑和时滞的复杂网络自适应同步控制研究

周武能 王天波 钟庆昌 方建安

(东华大学信息科学与技术学院，上海 201620 中国科学院上海微系统与技术研究所无线传感器网络与通信重点实验室，上海 200050) (东华大学信息科学与技术学院，上海 201620；上海工程技术大学基础教学学院，上海 200051) (拉夫堡大学航空与汽车工程学院，莱斯特 英国 LE11 3TU) (东华大学信息科学与技术学院，上海 201620)

利用 Lyapunov 稳定性理论、Kronecker 乘积分析技巧以及自适应控制方法，研究了具有切换拓扑和时滞(时滞同时包含离散和分布时滞，且网络拓扑结构不是固定不变的，而是按照Markov链进行切换)的复杂网络同步控制问题，给出了一些同步条件和自适应控制器的设计方法(此控制器依赖于滞后状态和Markov链)，最后以数值算例说明该方法的有效性。

自适应同步；复杂网络；时滞；Lyapunov 稳定性

近年来，随着因特网、万维网、电话网络等网络技术的发展和广泛应用，复杂网络已经成为科学研究和工程应用领域的一个热点问题[1～4]。网络同步作为网络最重要的一个动态行为，已经得到了广泛的研究，并取得了一些重要结果[5～10]。时滞作为网络中的常见现象，往往会导致网络在运行中出现振荡和不稳定。因此，对具有时滞的复杂网络同步问题研究具有重要的理论意义和应用价值[11～16]。

当前对复杂网络同步的研究主要是针对具有固定拓扑结构的网络[8,9,11]。然而，在实际应用中，还存在着大量拓扑结构随时间随机变化的网络，此时网络中节点的数量和连接边是随机变化的，于是对随机复杂网络的研究是必要的。文献[15]利用 Kronecker 乘积和随机分析工具，研究了复杂网络的指数同步问题，而且给出了网络同步条件；文献[16]采用分割时滞的方法，构造出一个新颖的Lyapunov 函数，得到了一类随机时滞复杂网络的同步条件。

下面，笔者利用自适应控制方法研究一类具有切换拓扑的时滞复杂网络同步问题，给出了一些关于具有切换拓扑的时滞复杂网络同步条件。

1 问题描述

用到的记号如下：Rn和Rn×m分别表示n维欧氏空间和n×m实矩阵；AT表示矩阵A的转置；对于给定的对称矩阵X和Y，X≥Y(Xgt;Y)表示X-Y是一个对称半正定矩阵(正定矩阵)；In表示n阶单位矩阵；“* ”表示矩阵中关于主对角线对称的元素；C(Rn,Rn)表示从Rn到Rn的连续向量值函数；⊗代表Kronecker乘积；λ(H)表示矩阵H的特征值。

考虑如下有N个节点通过线性耦合组成的复杂网络，每个节点是一个n维子系统：

Markov链σ(t)的状态转移概率矩阵∏=[πij]∈Rq×q满足：

(2)

式中：

(3)

πijgt;0(i≠j；i,j∈S)是从状态i到状态j的转移概率：

(4)

外耦合矩阵G(σ(t))=(gij(σ(t)))N×N∈RN×N和H(σ(t))=(hij(σ(t)))N×N∈RN×N代表网络的拓扑结构，并且按照Markov链σ(t)随机跳跃；gij(σ(t))和hij(σ(t))的定义如下：如果节点i和节点j之间存在信息交换，则gij(σ(t))=1或hij(σ(t))=1；否则，gij(σ(t))=0或hij(σ(t))=0，而且，矩阵G(σ(t))和H(σ(t))中的元素满足：

为描述方便，记：

σ(t)=r(r=1,2,…,q)

G(σ(t))=G(r)=GrH(σ(t))=H(r)=Hr

F(x(t))=(fT(x1(t)),fT(x2(t)),…,fT(xN(t)))T

则复杂网络(1)可以写成如下形式：

(5)

注1 与一些已有的复杂网络的结果(如文献[10,13～14])不同，网络(1)中外耦合矩阵是随机跃变而不是固定的，这更加符合实际。

设同步的目标节点是：

(6)

一般地，y(t)可能是系统的平衡点、周期环或者是混沌吸引子。笔者的目的是对每个节点设计自适应控制率ui(t)，使得复杂网络(1)与y(t)同步，即：

式(1)减去式(6)，且令ei(t)=xi(t)-y(t)，得：

即：

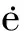
(8)

笔者所设计的自适应控制律为：

ui(t)=-ki(t)ei(t)-wi(t)ei(t-d)

式中，ki(t)和wi(t)是时变控制增益，满足：

(9)

(10)

式中，αi≠0,βi≠0(i=1,2,…,N)和Pr(r∈S)分别是待定的常数和对称正定矩阵。

自适应控制器式(9)和式(10)依赖于误差状态ei(t)和滞后ei(t-d)，如果将控制律写成：

ui(t)=-(ki(t)+wi(t))ei(t)+wi(t)(ei(t)-ei(t-d))

这正是文献[17]中的滞后型PID控制器。

2 假设条件和重要引理

假设1 对于给定的状态xi(t)和y(t)，非线性函数f(·)∈C(Rn,Rn)满足:

(xi(t)-y(t))TP[f(xi(t))-f(y(t))]≤-η(xi(t)-y(t))T(xi(t)-y(t))

式中,Pgt;0是对称正定矩阵;ηgt;0是已知常数。

假设2 复杂网络(1)是连通的，也就是说，网络中不存在孤立节点。

引理1 已知w(t):[hm,hM]→Rn是可积向量函数，则对于任意给定的正定矩阵Ω∈Rn×n和常数hmgt;0，hMgt;0,有：

式中，h1(t)和h2(t)是可微函数且满足0lt;hm≤h1(t)≤h2(t)≤hM。

引理2[20]Kronecker乘积⊗具有下列性质：

1)(A+B)⊗C=A⊗C+B⊗C,C⊗(A+B)=C⊗A+C⊗B;

2)(A⊗B)T=AT⊗BT;

3)(A⊗B)-1=A-1⊗B-1;

4)(A⊗C)(B⊗D)=AB⊗CD。

式中，A，B，C，D是具有适当维数的矩阵。

记：

K(t)=diag{k1(t),k2(t),…，kN(t)}⊗In

W(t)=diag{w1(t),w2(t),…,wN(t)}⊗In

E=(1,1,…,1)T∈RNΛα=diag{α1,α2,…,αN}Λβ=diag{β1,β2,…,βN}

1-h1=μ11-h2=d2μ2

则有：

式中，Pr,Q1,Q2,Q3是对称正定矩阵；IN是N阶单位矩阵。

3 主要结论

定理1 在假设1和假设2下，如果存在正定对称矩阵Q1gt;0,Q2gt;0,Q3gt;0,Prgt;0(r∈S)和常数αi≠0，βi≠0(i=1,2,…,N)，ηgt;0满足：

(11)

证明取Lyapunov函数为：

V(t)=V1(t)+V2(t)

将V1(t)和V2(t)分别沿系统(8)的状态轨线求导，得:

=eT(t)(IN⊗Pr)[F(x(t))-F(y(t))+c1(Gr⊗Γ1)e(t-τ1(t))

-eT(Λα⊗Pr)e(t)-eT(Λβ⊗Pr)e(t-d)

(12)

根据假设1，有：

eT(t)(IN⊗Q1)(F(x(t))-F(y(t)))≤-ηeT(t)e(t)=-ηeT(t)(IN⊗In)e(t)

利用式(12)～(16)，得：

(17)

式中：

再利用Schur补引理可知，如果不等式(11)成立，则ψlt;0。所以：

注3 在定理1的证明中，笔者用的是完全平方公式而不是不等式±2aTb≤aTPa+bTP-1b，这样得到的结果具有较小的保守性。

作为一个特例，当σ(t)=1时，可以得到如下的推论。

推论1 在假设1和假设2下，如果存在正定对称矩阵Q1gt;0,Q2gt;0,Q3gt;0,Pgt;0和常数αi≠0,βi≠0(i=1,2,…,N)，ηgt;0满足：

(18)

则复杂网络：

(19)

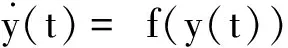
当自适应控制律不含时滞项时，即ui(t)=-ki(t)ei(t)，有如下推论。

推论2 在假设1和假设2下，如果存在正定对称矩阵Q1gt;0,Q2gt;0,Prgt;0(r∈S)和常数αi≠0(i=1,2,…,N)，ηgt;0满足：

(20)

注4 利用Matlab中的mincx命令，可以通过求解不等式(11)得到η的最优值。

4 数值算例

考虑一个由5个节点，每个节点都是三维子系统以及2个切换模态构成的复杂网络(1)，函数f(xi)=(-2.5xi1,-2xi2,-3xi3)T，当取η=3,c1=0.4,c2=0.7时，假设1满足。假定外耦合矩阵分别是：

图1 目标节点的状态轨线

利用Matlab中的线性矩阵不等式工具箱，可以得到不等式(11)的可行解为:

P1=diag{0.0602,0.0648,0.0654}

P2=diag{0.0503,0.0574,0.0621}

Q1=diag{0.7842,0.7994,0.8200}

Q2=diag{0.7524,0.7449,0.7292}

Q3=diag{0.8652,0.8864,0.8964}

在自适应控制律的作用下，误差系统(8)的状态轨线如图2和图3。图2表明误差系统是稳定的，5个节点是同步的。图3表明当网络达到同步后，控制器的增益为常数。

图2 误差系统的状态轨线(i=1,2,…,5)

5 结 语

利用 Lyapunov-Krasovskii 稳定性理论，完全平方公式和 Kronecker 乘积分析技巧，研究了具有切换拓扑和时滞的复杂网络自适应同步控制问题，得到了网络同步的一些条件和控制器的设计方法。数值仿真说明笔者的方法是有效的。

[1]Watts D J, Strogatz S H.Collective dynamics of small world networks[J].Nature,1998,393:40～442.

[2]Jeong H, Tombor B, Albert R,etal.The large-scale organization of metabolic networks[J].Nature, 2000, 407:651～654.

[3]Jin C W,Marsden I, Chen X Q,etal.Dynamic DNA contacts observed in the NMR structure of winged helix protein-DNA complex[J].J Mol Biol，1999，289：683～690.

[4]Li Z, Chen G.Global synchronization and asymptotic stability of complex dynamical networks[J].IEEE Transactions ASCII,2006,53：28～33.

[5] Perales G S, Velazquez E R, Rodriguez D V. Synchronization in complex networks with distinct chaotic nodes[J]. Commun Nonlinear Sci Numer Simulation, 2009,14:2528～2535.

[6] Wang L, Dai H, Sun Y.Synchronization criteria for a generalized complex delayed dynamical network model[J]. Physica A， 2007,383: 703～713.

[7]Zhou J L J.Pinning adaptive synchronization of a general complex dynamical network[J].Automatica,2008, 44:996～1003.

[8]Yu W, Cao J, Chen G,etal.Local synchronization of a complex network model[J].IEEE Transactions on Systems, Man, and Cybernetics-Part B: Cybernetics, 2009,39:230～241.

[9]Dai Y, Cai Y, Xue X. Synchronization criteria for complex dynamical networks with neutral-type coupling delay[J].Physica A， 2008,387 :4673～4682.

[10]Liu Y R, Wang Z D, Liu X H. Exponential synchronization of complex networks with Markovian jump and mixed delays[J].Physics Letters A, 2008,372:3986～3998.

[11]Liu H, Lu J, L J,etal.Structure identification of uncertain general complex dynamical networks with time-delay[J].Automatica,2009,45:1799～1807.

[12]Lu W L, Chen T P. Global synchronization of discrete-time dynamical network with a directed graph[J].IEEE Transactions on Circuits System II: Express Briefs, 2007,54:136～140.

[13]Liu Y R, Wang Z D, Liang J L,etal.Synchronization and state estimation for discrete-time complex networks with distributed delays[J]. IEEE Transactions on Systems, Man, and Cybernetics-Part B: Cybernetics,2008,38: 1314～1325.

[14]Fei Z Y, Gao H J, Zheng W X.New synchronization stability of complex networks with an interval time-varying coupling delay[J].IEEE Transactions on Circuits and System-II: Express Briefs，2009,56:499～503.

[15]Wei, G L, Wang Z D, Lam J,etal.Robust filtering for stochastic genetic regulatory networks with time-varying delay[J].Mathematical Biosciences, 2009,220:73～80.

[16]Wang Y, Wang Z D, Liang J L.A delay fractioning approach to global synchronization of delayed complex networks with stochastic disturbances[J].Physics Letters A，2008,372:6066～6073.

[17]Lu W, Chen T. New approach to synchronization analysis of linearly coupled ordinary differential systems[J].Physica D，2006,213:214～230.

[18] Han Q L, Jiang X F, Ma X.Computation of delay bound for linear neutral systems with interval time-varying discrete delay[J].Dynamics of Continuous, Discrete and Impulsive Systems,2006,13:117～131.

[19] Li Z K, Duan Z S, Chen G R,etal.Consensus of multi-agent systems and synchronization of complex networks: a unified viewpoint[J]. IEEE Transactions on Circuits and Systems I: Regular Papers，2010,57:213～224.

[20] Kolmanovskii V B, Myshkis A D. Introduction to the theory and application of functional differential equations[M].Norwell, MA: Kluwer, 1999.

[21]Zhong Q C, Li H X. A delay-type PID controller[A].15th Triennial World Congress of the International Federation of Automatic Control[C].Barcelona,2002.

[编辑] 洪云飞

O231.5

A

1673-1409(2010)03-N001-08

2010-06-27

国家“863计划”项目(2008AA042902)；国家自然科学基金资助项目(61075060，60874113)；中国高等教育博士研究基金项目(200802550007)；上海市教委科学研究和创新项目(09ZZ66)；上海市基础研究项目(09JC1400700)；工业控制技术国家重点实验室开放基金项目。

周武能(1959-)，男，1982年大学毕业，博士，教授，现主要从事复杂网络稳定性与同步、随机系统分析与综合、鲁棒H无穷控制等方面的教学与研究工作。