裂隙岩体声波传播特征数值模拟研究

2010-11-27贾善坡张艳娜

长江大学学报(自科版) 2010年7期

关键词：波幅倾角投影

贾善坡，王强张艳娜

(长江大学城市建设学院，湖北荆州 434023) (中国石油勘探开发研究院，北京 100083)

裂隙岩体声波传播特征数值模拟研究

贾善坡，王强张艳娜

(长江大学城市建设学院，湖北荆州 434023) (中国石油勘探开发研究院，北京 100083)

以工程中常见的裂隙岩体为研究对象，采用显式动力有限元法研究了不同长度、宽度、倾角、密度、形态(连续与断续)的裂隙对岩体声波传播特性的影响，测试了声波在裂隙介质中的衰减规律。以ABAQUS为数值分析平台，对裂隙介质中的声波传播过程进行数值仿真分析。结果表明，波幅的衰减取决于垂直于波传播方向的裂隙水平投影长度，裂隙水平投影长度越大，波幅衰减量越大；波幅衰减几乎不受裂隙宽度的影响；随着裂隙密度的增加，波幅衰减速度明显加快；裂隙形态(连续与断续)对波幅影响不大。将模拟结果与相关试验进行对比，发现数值模拟和相关试验结果符合较好。

裂隙岩体；非贯通裂隙；波传播；数值仿真；波幅衰减

岩石是矿物的集合体，它是由多种矿物、裂隙等组成的多相体。裂隙的存在是岩石结构的重要特点，由于岩石中裂隙的存在，才有可能蕴藏地下水、石油、天然气和其他矿产资源。裂隙的数目及破坏程度等造成了岩石微结构的不均匀性和复杂性。应力波传播过程中遇到岩体中裂隙，应力波能量的传播会有很大衰减，岩体中裂隙的分布形式和尺寸对岩体中应力波传播具有很大影响。针对裂隙岩体的波传播问题，学者们开展了大量的工作，并取得了一定的研究成果。王卫华[1]预制含不同锯齿的人工裂隙试样，并研究了应力波在人工裂隙试样中的传播问题；邓向允等[2]研究含不同缺陷的玄武岩、水泥砂浆和混凝土等声波频散效应，认为裂隙密度等对玄武岩频散效应有很大影响；Hudson[3]通过数值分析方法给出分布大尺度裂隙的介质位移与应力之间的关系。实际上，岩体是含各种各样细观结构、裂隙和孔洞等缺陷的复杂结构体，同时由于地应力的存在，岩体一般处于复杂的应力状态，其响应非常复杂，很难用确定性模型准确描述[4～6]。

在工程实践中，广泛存在着裂隙岩体，岩体声波测试成为评价岩体完整性和岩体质量的重要指标之一，同时，应力波在岩石介质中的传播也是岩石动力学的重要课题。应力波在岩石介质中的传播性质，取决于岩石介质的内在特征。因此，研究裂隙的分布形式和尺寸对应力波传播规律的影响具有重要意义，但由于裂隙分布的随机性及位置的不确定性，对于裂隙岩体中的波传播特性进行现场试验研究是很困难的。笔者通过数值模拟，采用大型有限元软件ABAQUS对含有一定几何分布特征的裂隙模型的应力波传播特性进行了系统研究。

1 弹塑性波传播的有限元方程

2.1动力平衡方程

用虚功原理可以导出材料非线性问题的物理动力平衡方程，在只考虑面力荷载时，虚功方程为[7]：

(1)

式中,{σ}、{f}和{u}分别为应力、面力和位移向量；下标t或t+τ表示时刻；{δεL}和{δu}分别为虚应变和虚位移向量；ρ为密度，kg/m3；Δ表示增量。

引入插值函数，用节点位移表示内点位移，并引入几何方程和非线性的物理方程，将上述的虚功方程离散化，可得到有限元的动力平衡方程：

(2)

式中,[M]为整体质量矩阵；[K]NL为整体非线性刚度矩阵；[Ft]为t时刻的节点内抗力向量；{Rt+τ}为t+τ时刻的等效节点外荷载向量。

2.2本构方程和屈服准则

岩体具有很强的非线性效应，其压缩模量和变形的历史相关。一般情况下可采用Prandtl-Reuss流动理论[8]给出以增量形式表述的本构关系，即：

{dσ}=[Dep]{dε}

(3)

式中,弹塑性矩阵[Dep]为：

式中，De为弹性矩阵；F为屈服函数；A为加工硬化模量，只与材料的种类有关，可由试验确定。可见只要选用一个屈服函数，即可通过式(3)导出不同状态下的弹塑性矩阵的具体表达式。

在岩体中，为了考虑平均压力的影响，一般采用Drucker-Prager屈服准则[8]：

(4)

式中，a、K与岩体介质的内摩擦角和粘聚力有关。

2.3数值积分方法和迭代求解法

采用Newmark法对动力平衡方程逐步积分，取δ=0.5，a=0.25，式(2)可写为：

(8)

式(8)为增量的非线性方程组。t+Δt时刻的待求运动量为：

(9)

(10)

ut+Δt=ut+Δu

(11)

采用修正的牛顿迭代法求解。迭代公式为：

(12)

式中，i为迭代次数，该迭代公式只在每个时步开始时重新计算刚度矩阵。用位移收敛准则来保证得到平衡状态的解，允许误差取为1%。

3 裂隙分布对声波传播的影响

图1 数值模拟模型

3.1数值模拟模型

将数值模拟模型长度取为0.5m，宽度为0.12m，如图1所示。在模型的一端输加动态荷载，从而引起向另一端传递的应力波，取模型的形心为中心点，通过中心点处的应力波来研究裂隙的几何特征(长度、宽度、倾角和密度)对波传播的影响。

3.2数值模拟方案

1)裂隙的倾角(裂隙方位与垂向的夹角)α= 0°，厚度为0.3mm，长度分别为12、25、39、54、66、77和92mm。

2)裂隙长度为54mm，厚度为0.3mm，倾角分别为 0、30、45、60和90°。

3)裂隙长度为54mm，倾角α=0°，厚度分别为0.1、0.2、0.3、0.4和0.5mm。

4)裂隙长度为54mm，厚度为0.3mm，倾角α=0°，分别建立含 1、2 、3、4和5排裂隙的模型。

5)裂隙长度为54mm，厚度为0.3mm，倾角α=0°，分别建立1段(长为54mm)、2段(每段长为27mm)、4段(每段长为13.5mm)的裂隙模型。

3.3结果分析

图2 裂隙长度对波幅透射系数的影响

1)裂隙长度的影响定义含裂隙模型的应力波波幅与完整模型应力波波幅的比值A/A0为波幅透射系数，得到波幅透射系数随裂隙长度变化曲线，如图2所示。由图2可以看出，在固定单条裂隙的倾角α=0°、厚度为0.3mm不变时，随着裂隙长度的增加，透过裂隙所接收到的应力波波幅线性减小。这是由于随裂隙长度的增加，更多的应力波能量被裂隙所阻挡而不能透过，故测得的应力波波幅随裂隙长度的增加而减小，即波幅透射系数A/A0随裂隙长度增加而减小，且应力波波幅与裂隙长度成反比关系。

2)裂隙厚度的影响当固定单条裂隙长度为54mm、倾角均为0°时，改变裂隙厚度，研究裂隙厚度对应力波在裂隙中传播的影响。采用的裂隙厚度分别为0.1、0.2、0.3、0.4和0.5mm。不同裂隙厚度模型模拟结果如表1所示。由表1可以看出，在裂隙长度相同的情况下，在5种不同厚度的裂隙中，应力波波幅相差不大，可见裂隙厚度的变化对波幅影响很小。

3)裂隙倾角的影响对长度为54mm、厚度为0.3mm的单条裂隙在不同倾角下进行模拟，其结果如表2所示。由表2可以看出，裂隙倾角对应力波的影响可以近似转化为垂直投影长度对应力波的影响，裂隙垂直投影长度越大，波幅越小，波幅与裂隙垂直投影长度成反比关系。

表1 不同裂隙厚度模型模拟结果

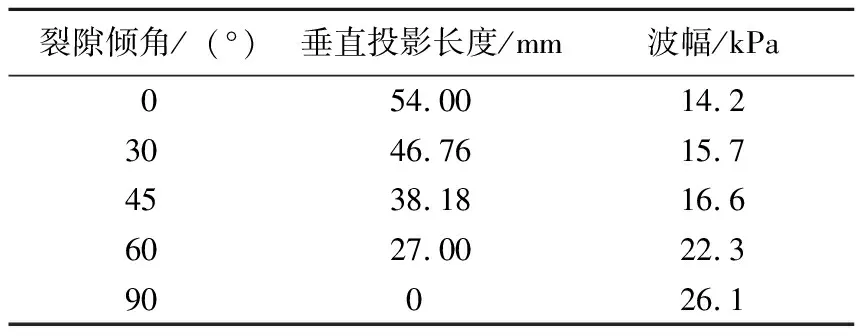
表2 不同裂隙角度模型模拟结果

4)裂隙密度的影响固定裂隙长度为54mm、厚度为0.3mm，倾角α=0°不变，改变裂隙的排数，研究裂隙密度对波幅的影响。结果表明，随着裂隙排数的增加，波幅快速衰减，且应力波波幅与裂隙排数成反比关系(如图3所示)。这是由于通过第1排裂隙，应力波波幅受裂隙影响衰减一部分，当通过第2排裂隙时，透射过第1排裂隙的应力波波幅又要损失一部分，同样通过第3排裂隙时，还要减少一部分。故随着裂隙密度(排数)的增加，透射过去的波幅(能量)随之减小。

5)裂隙形态(连续与断续)的影响固定裂隙总长度为54mm，厚度为0.3mm，倾角α=0°不变，改变裂隙的段数，研究裂隙形态(连续与断续)对波幅透射系数的影响，如图4所示。从图4可以看出，在裂隙总长一定、改变裂隙段数的情况下，应力波幅透射系数A/A0变化很小。对波幅透射值起决定作用的是裂隙的总长度，而与裂隙形态关系不大。因此，裂隙形态对应力波幅影响不大。

图3 裂隙密度对波幅的影响图4 裂隙形态对波幅透射系数的影响

6)数值模拟结果与试验结果的对比邓向允等[2,9]进行了玄武岩中裂隙分布形式对声波传播的影响室内试验。试验结果表明，当裂纹方向与波传播方向垂直时，散射效应最大，波幅有很大的衰减；当裂纹方向与波传播方向平行时影响最小，波幅衰减不很明显。笔者进行的数值模拟结果显示，当裂纹方向与波传播方向垂直时，波幅最小为14.2kPa，衰减最大；当裂纹方向与波传播方向平行时，波幅最大为26.1kPa，衰减不明显，数值模拟结果和试验结果一致。另外，室内试验表明，随着裂隙垂直波传播方向长度的增加，衰减量也愈大，裂隙平行波传播方向的长度没有造成波幅的大幅度衰减。而数值模拟结果显示，裂隙倾角对应力波的影响作用可以近似转化为垂直投影长度对波的影响，裂隙垂直投影长度越大，波幅越小，波幅衰减量与裂隙垂直投影长度成反比关系，数值模拟结果也和试验结果一致。