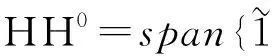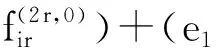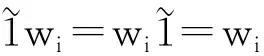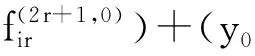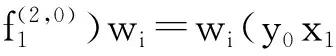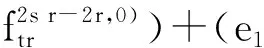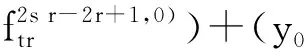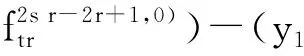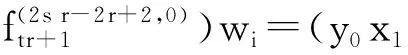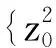量子外代数的2-Galois覆盖的Hochschild上同调环
2010-11-26汪俊
汪俊
(湖北大学 数学与计算机科学学院,湖北 武汉 430062)
0 引言
设Λ是域k上的有限维结合代数(含单位元1).它的包络代数定义为Λe=Λop⊗kΛ,其中Λop是Λ的反代数.则Λ是右Λe-模,通篇路的合成采用从左到右的顺序.Λ第n阶Hochschild上同调群定义为[1]
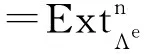
Hochschild上同调是结合代数较精细的不变量,如Marita等价不变量,Tilting等阶不变量,及导出等价不变量等等.且它在Artin代数的表示理论中扮演着重要的角色,例如,它和代数的单连通性,可分性质及形变理论密切相关[2-7].
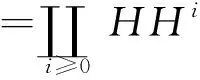
Koszul代数在表示理论的研究中扮演着重要的角色.量子外代数Aq=k〈x,y〉/(x2,xy+qyx,y2)是一类有趣的Koszul代数[14-15].设Λq为Aq的2-Galois覆盖,韩阳在文献[16]中证明Λq也是Koszul代数.本文中首先计算出了Λq的各阶Hochschild上同调群的k-基;其次,由于Buchweitz等人用Yoneda积描述的Λq的上同调环的乘法结构较抽象,本文中用平行路的语言刻画了上同调环的乘法结构,且在此基础上,找出了HH*(Λ)的生成元及关系.
1 Hochschild上同调群的k-基
这一节,我们将给出覆盖代数Λq的各阶Hochschild上同调群的k-基.对于kQ中的任意非零元素x,如果在Q0中存在点u和v,使得x=uxv,则称x为一致(uniform)的.设X,Y是kQ中的一致元素组成的集合,记X∥Y={(x,y)∈X×Y|o(x)=o(y)且t(x)=t(y)},则(x,y)∈X∥Y称为平行路,并记k(X∥Y)是以X∥Y为基的k-向量空间.
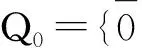
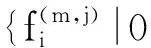
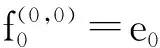
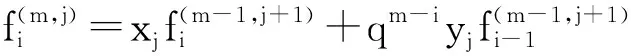
(1)
下面我们可以给出Λ在Λe上的一个极小投射双模分解
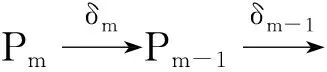
将函子HomΛe(-,Λ)作用于极小投射双模分解( P·,δ·),则有下面引理.
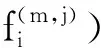
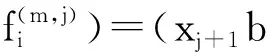
欲找出Λ的各阶上同调群的k-基,由公式HHm(Λ)=Kerσm+1/Imσm知,我们需找出子空间Kerσm+1和Imσm的k-基.
显然,对任意的(b,f)∈B∥Γ(m),易知l(b)和m具有相同的奇偶性,因此dimkMm=4(m+1).
对m=0,1,2,直接计算可得
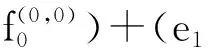
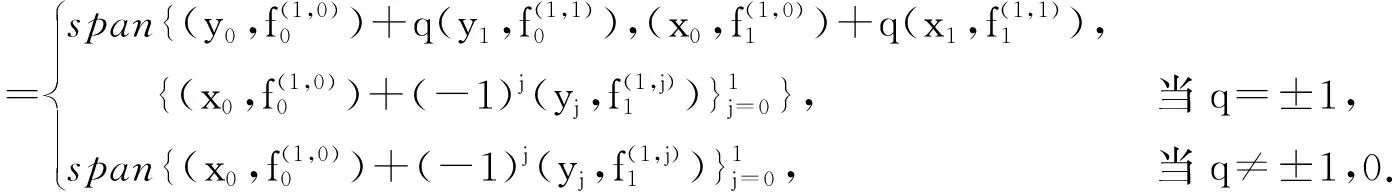
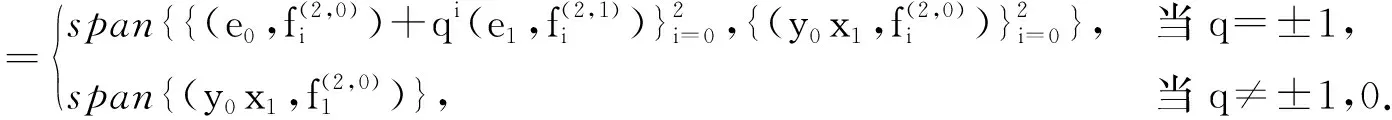
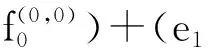
欲找出Λ高阶的Hochschild上同调群的k-基,我们需要对q进行分类讨论,即
当q≠0不是单位根时,有下列引理.
引理1.2 如果q≠0不是单位根,则HHm(Λ)=0(m>2).
当q≠0是单位根时,将分下面3种情况进行讨论:(1)q≠0是一个r次本原单位根且r为奇数(r>2);(2)q≠0是一个r次本原单位根且r为偶数(r>2);(3)q=±1.
引理1.3 如果q≠0是一个r次本原单位根(r>2)且r为奇数,则对于m>2,
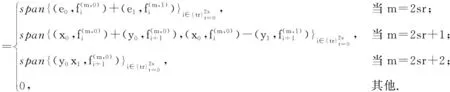
引理1.3的证明由已有文献知
又因为dimkKerσm+1+dimkImσm+1=dimkMm=4(m+1),所以
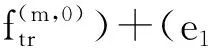
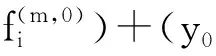
类似地,我们有下列引理.
引理1.4 如果q≠0是一个r次本原单位根(r>2)且r为偶数,则对于m>2,
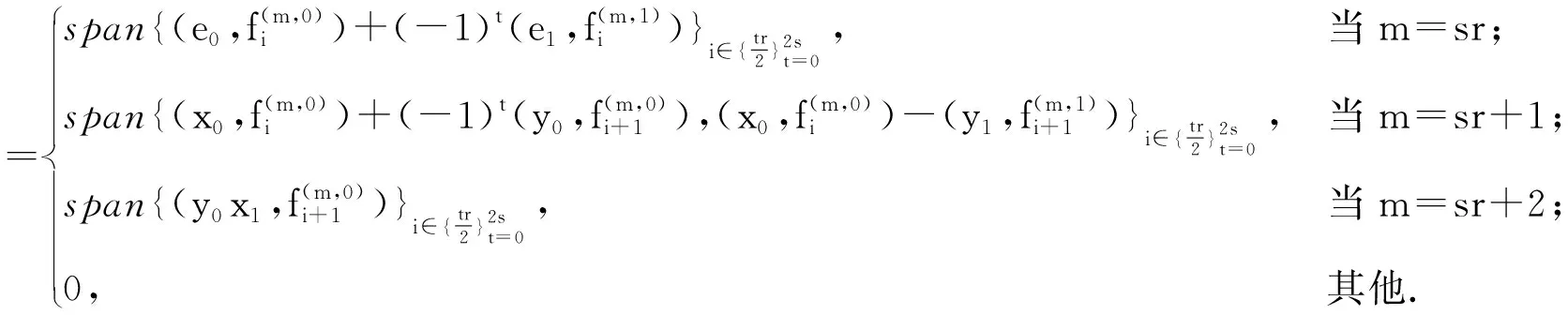
引理1.5 如果q=±1,则对于m>2,
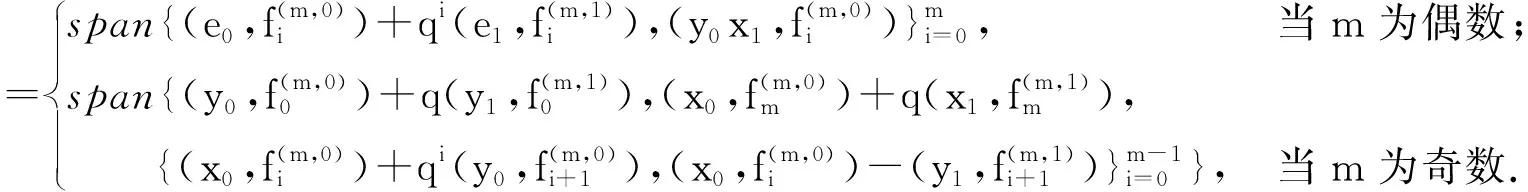
2 乘法结构
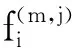
引理2.1的证明对r作归纳法.
(1)当r=0时,结论显然成立.当r=1时
所以r=1时,结论成立.
(2)假设该式对于≤r-1时均成立,下证对于r也成立.
由假设,有
(*)
(a)0≤i≤r-1时.
(*)式变为
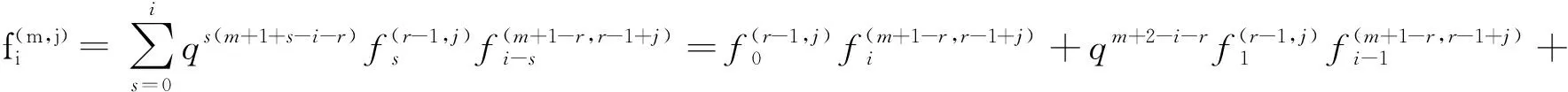
(b)r-1 (*)式变为 (c)m-r+1≤i≤m时. (*)式变为 下面定义平行路的乘法. 我们将向量空间HomΛe(Pm,Λ)到k(B∥Γ(m))的同构映射及其逆映射分别记为φ与ψ[18],Yoneda积记为*,则有下列定理. 因为Λ是Koszul代数,对于任意的η∈HomΛe(Pn,Λ),θ∈HomΛe(Pm,Λ),它们的Yoneda积η*θ可由下面的映射合成 另一方面 这一节我们将给出覆盖代数Λq的Hochschild上同调环的结构.如果R→k,S→k是两个环同态,记R与S的纤维积为R×kS. 下面我们通过对q分类讨论给出Λq的Hochschild上同调环HH*(Λq)的结构.将HH*(Λq),HHn(Λq)分别简记为HH*,HHn. 定理3.1 设Λq是二元量子外代数Λq的2-Galois覆盖.如果q≠0不是单位根,则HH*作为环同构于纤维积k[z0,z1]/,z0z1,×kΛ*(u0,u1),其中Λ*(u0,u1)是由u0,u1生成的二元外代数. 引理3.2 如果q≠0是一个r次本原单位根(r>2),且r为奇数,则HH2s r=HH2(s-1)r∨HH2r,HH2s r+1=HH2(s-1)r+1∨HH2r,HH2s r+2=HH2(s-1)r+2∨HH2r,s≥1. 下面通过对s作归纳法进行证明. s=1时,由定义2.2给出的乘法有如下乘法表. 根据引理1.3有,HH2r=HH0∨HH2r,HH2r+1=HH1∨HH2r,HH2r+2=HH2∨HH2r.故结论成立. 假设对于 再根据引理1.3有,HH2s r=HH2(s-1)r∨HH2r,HH2s r+1=HH2(s-1)r+1∨HH2r,HH2s r+2=HH2(s-1)r+2∨HH2r.证毕. 同理有如下两个引理. 引理3.3 如果q≠0是一个r次本原单位根(r>2)且r为偶数,则HHs r=HH(s-1)r∨HHr,HHs r+1=HH(s-1)r+1∨HHr,HHs r+2=HH(s-1)r+2∨HHr,s≥1. 引理3.4 如果q=±1,则HH2k+1=HH2k-1∨HH2,HH2k+2=HH2k∨HH2,k≥1. 定理3.5 设Λq是二元量子外代数Aq的2-Galois覆盖,如果q≠0是一个r次本原单位根(r>2),且r为奇数,则HH*作为环同构于纤维积k[z0,z1]/,z0z1,×k(Λ*(u0,u1)[w0,w1,w2]/,其中wi=(e0,,,i=0,1,2,Λ*(u0,u1)是由u0,u1生成的二元外代数. 根据引理3.3和定义2.2,类似地我们有下面的定理. 定理3.6 设Λq是二元量子外代数Aq的2-Galois覆盖,如果q≠0是一个r次本原单位根(r>2)且r为偶数,则HH*作为环同构于纤维积k[z0,z1]/,z0z1,×k(Λ*(u0,u1)[w0,w1,w2]/,其中wi=(e0,,i=0,1,2,l≡r(mod4),Λ*(u0,u1)是由u0,u1生成的二元外代数. 根据引理3.4和定义2.2,即有下列定理. 定理3.7 设Λq是二元量子外代数Aq的2-Galois覆盖,如果q=±1,则HH*作为环同构于纤维积,w1,w2]/Iq,其中u2=(y0,,,u3=(x0,,,wi=(e0,,,i=0,1,2,Λ*(u0,u1,u2,u3)是由uk,k=0,1,2,3生成的外代数,理想Iq由集合Rq={z0wi-qz1wi,u0u2+z0w0,u1u2+z0w0,u2u3-2qz0w1,u0u1-qz0w1,u0u3-qz0w2,u1u3+qz0w2,u2w1+q(u1w0-u0w0),u2w2+u1w1-u0w1,u3w0-q(u0w1+u1w1),u3w1-u0w2-u1w2,生成,i=0,1,2. 参考文献: [1] Cartan H,Eilenberg S.Homological algebra[M].Princeton NJ:Princeton University Press,1956. [2] Happel D.Hochshcild cohomology of finite-dimensional algebras[R].Springer Lecture Notes in Math,1404,Berlin:Springer,1989:108-126. [3] Skowroński A.Simply connected algebras and Hochschild cohomology[J].Proc ICRA IV(Ottawa,1992),Can Math Soc Proc,1993,14:431-447. [4] Assem I,de la Pea J A.The foundamental groups of a triangular algebra[J].Comm Algebra,1996,24:187-208. [5] Cibils C.Rigid monomial algebras[J].Math Ann,1991,289:95-109. [6] Cibils C.Rigidity of truncated quiver algebras[J].Adv Math,1990,79:18-42. [7] Gerstenhaber M.On the deformation of rings and algebras[J].Ann Math,1964,79:59-103. [8] Siegel F S,Witherspoon S J.The Hochschild cohomology ring of a group algebra[J].Proc London Math Soc,1999,79(3):131-157. [9] Xu Y G,Han Y.Hochschild(co)homology of exterior algebras[J].Comm Algebra,2007,35(1):115-131. [10] Bustamante J C.The Hochschild cohomology ring of string algebras[J].Journal of Pure and Applied Algebra,2006,204(3):616-626. [11] Cibils C.Hochschild cohomology algebra of radical sequare zero algebras[J].CMS Conf Proc,1998,24:93-101. [12] Green E L,Snashall N,Solberg Ø.The Hochschild cohomology ring of a self-injective algebra of finite representation type[J].Proc Amer Math Soc,2003,131:3 387-3 393. [13] Green E L,Solberg Ø.Hochschild cohomology rings and triangular rings[C]//In:Happel D,Zhang Y B,eds.Proceedings of the Ninth International Conference,vol 2.Beijing:Beijing Normal University Press,2002,192-200. [14] Buchweitz R O,Green E L,Madsen D,et al.Finite Hochschild cohomology without finite global dimension[J].Mathematical Research Letters,2005,12:805-816. [15] Beilinson A,Ginsburg V,Soergel W.Koszul duality patterns in representation theory[J].J Amer Math Soc,1996,9:473-527. [16] Han Y,Zhao D K.Construction of Kosztd algebras by finite Galois covering[EB/OL].arXiv:math.RA/0605773. [17] Auslander M,Reiten I,SmalØ S O.Representation theory of artin algebraS[M].Cambridge:Cambridge University Press,1995. [18] 董培佩,徐运阁,侯波.Koszul 代数的 Hochschild 上同调环[J].数学学报,2008,51(6):115-116.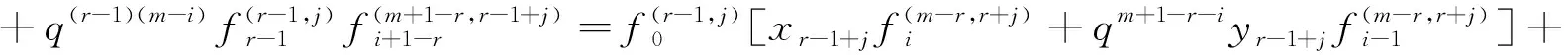
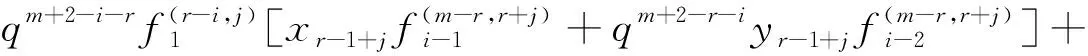
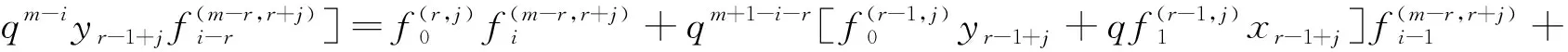
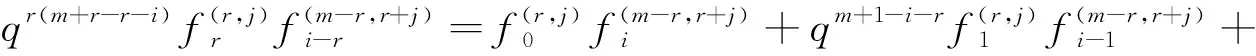
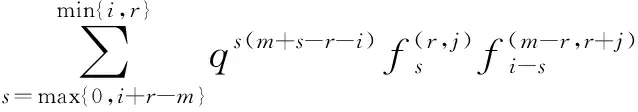
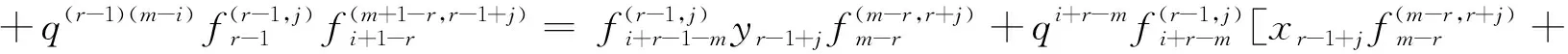
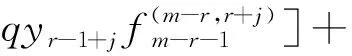
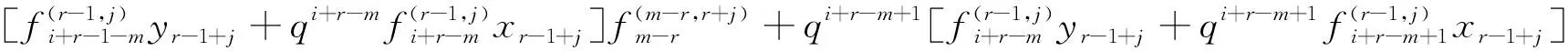
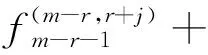
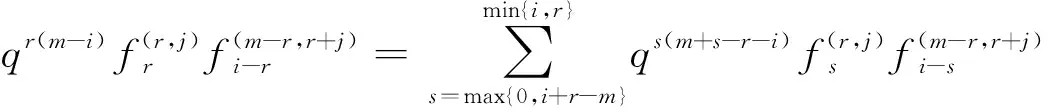
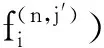
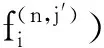
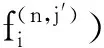
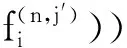
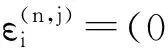
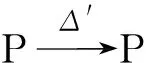
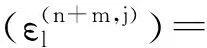
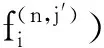
3 上同调环的结构