基于数值分析聚合物共挤出工艺的探讨

程蕾,闫普选

(1.广西师范大学 科技处,广西 桂林 541004;2.中国化学工业桂林工程公司,广西 桂林 541004)

挤出成型是聚合物最基本的成型方法之一[1].为了得到具有特殊性能和外观的橡塑制品,工业生产中常采用共挤出工艺,该工艺能够实现不同性能聚合物的有机复合.然而,复合制品性能及尺寸的稳定性,不仅取决于复合挤出机头流道结构的优化,还取决于工况条件的科学筛选和聚合物的种类.

传统筛选工艺参数的挤出实验,因调整挤出工艺时间长且成本高而不能满足工业生产需求.数值分析作为科学的工艺设计工具,能够快速解析工艺参数与挤出结果之间的规律性关系[2],为工艺设计提供理论指导,其中有限元数值分析方法能够对工艺参数与挤出结果进行定量分析[3],在理论上优选共挤出工艺,从而加速产品的更新速度.

本文中以多流道共挤出工艺为研究对象,根据聚合物流体本构方程,采用有限元方法分析不同工艺条件下典型聚合物在挤出机头流道中的等温流变行为,解析聚合物流体流道出口的速度场,从而优选共挤出工艺,为多流道共挤出工艺提供理论依据,避免单凭经验设计工艺的盲目性.

1 实验部分

1.1主要原料PS,广州市华立颜料化工实业公司,密度1.05×103kg·m-3;PP,扬子石化巴斯夫有限公司,密度0.90×103kg·m-3;PVC,石家庄驰瑞化工科技有限公司,密度1.45×103kg·m-3;NR,广州建维化工有限公司,密度0.925×103kg·m-3.

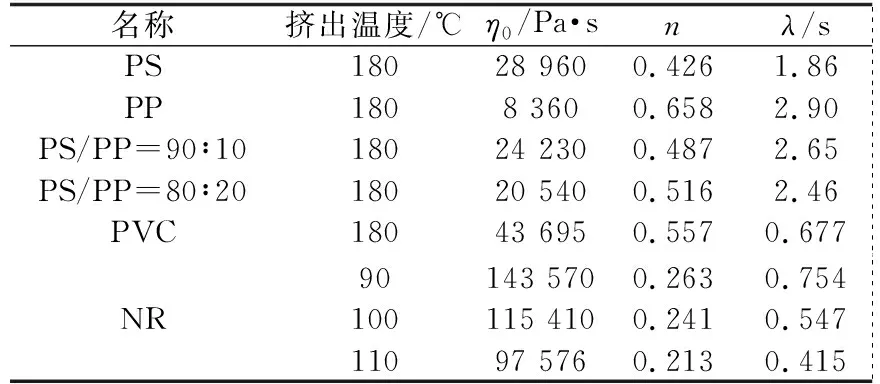
表1 不同聚合物对应cross本构方程的参数

1.2成型工艺将PS和PP原料用真空干燥箱烘干后,按一定的比例均匀的混合,用双螺杆挤出机挤出,造粒,烘干备用.

1.3流变性能测试采用CFT-500D型毛细管流变仪测试聚合物的流变性能,毛细管直径1.0 mm,长度10.0 mm,预热时间30 s,聚合物测试温度如表1所示.流体本构方程采用cross模型,其公式为[4]:

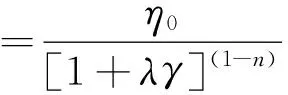
(1)

式中:η为粘度,Pa·s;η0为零剪切粘度,Pa·s;λ为松弛时间,s;n为非牛顿指数,无因次;γ为剪切速率,s-1.

通过毛细管流变仪测试聚合物流体表观粘度和剪切速率的数据,采用统计软件拟合不同聚合物cross本构方程的参数,具体如表1所示.

2 物理模型

2.1三流道共挤出流道结构对于多层复合材料的制备工艺,传统共挤工艺和气辅共挤工艺均需调节工艺参数来优化材料性能,其性能体现在复合材料中不同聚合物的厚度比和界面稳定性.研究表明[5],当不同聚合物流体的速率比为1时,复合材料性能达到最优化.本文中以三流道共挤出片材机头为例,由图1所示,三股不同物理性质的聚合物流体从不同入口流入流道,在进入交汇点之前扩展成平板流体;同时,平板流体速率相对偏差尽量小.此时定量分析挤出工艺参数与聚合物流体出口速率的对应关系,从而优化复合材料的性能.

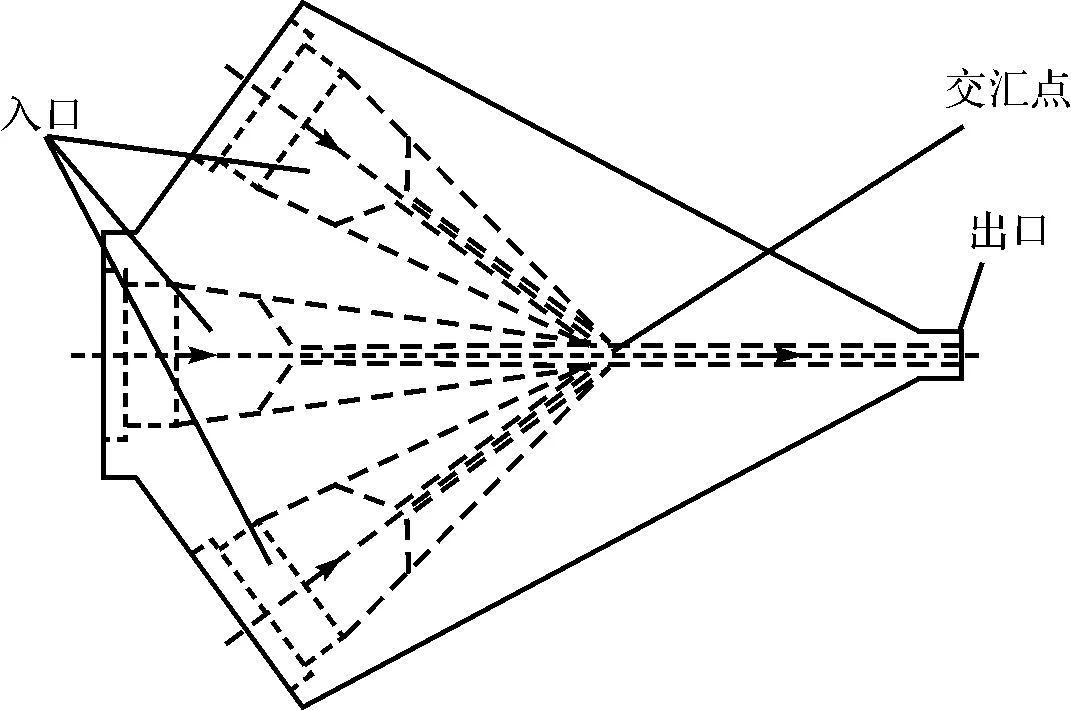
图1 三流道共挤出流道结构

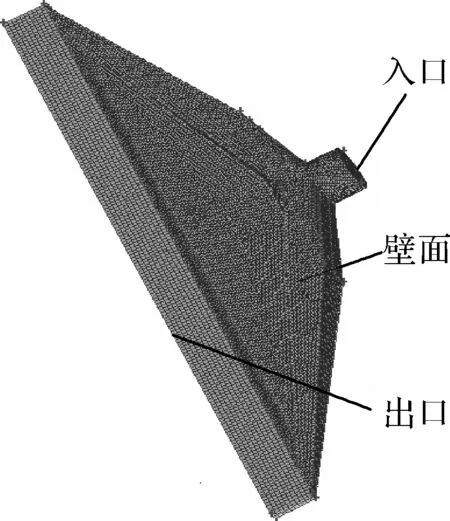
图2 挤出流道网格及边界条件

2.2挤出流道网格及边界条件为提高计算效率,以中流道为例分析流体交汇前的流道出口速度场,从而对各聚合物出口速率进行定量分析.

为便于有限元数值分析,假设流道中流体为不可压缩流体,其流动为等温稳态流动,流道全充满,同时流道内壁无滑移[6].因流体粘度大,惯性力和重力相对于粘性力可忽略不计.图2表明了挤出流道求解域的三维网格图,其实际边界条件如下:

1) 流道入口采用压力入口边界条件,压力由挤出工艺设定;

2) 流道出口采用压力出口边界条件,压力为1个大气压;

3) 其余为壁面,设置为非滑移边界条件.

3 结果与讨论

3.1入口压力对流道出口PVC流体速率的影响图3为在其他工况相同情况下不同入口压力对应流道出口PVC流体速率曲线.由图可知,各曲线依次代表入口压力为15 MPa、20 MPa和25 MPa时流道出口PVC流体的速率曲线,随着入口压力的增加,流体的速率逐步上升,同时出口速率相对偏差(分别为2.1%、1.8%和1.5%)逐渐减小,从而流道出口速率的均匀性增加.

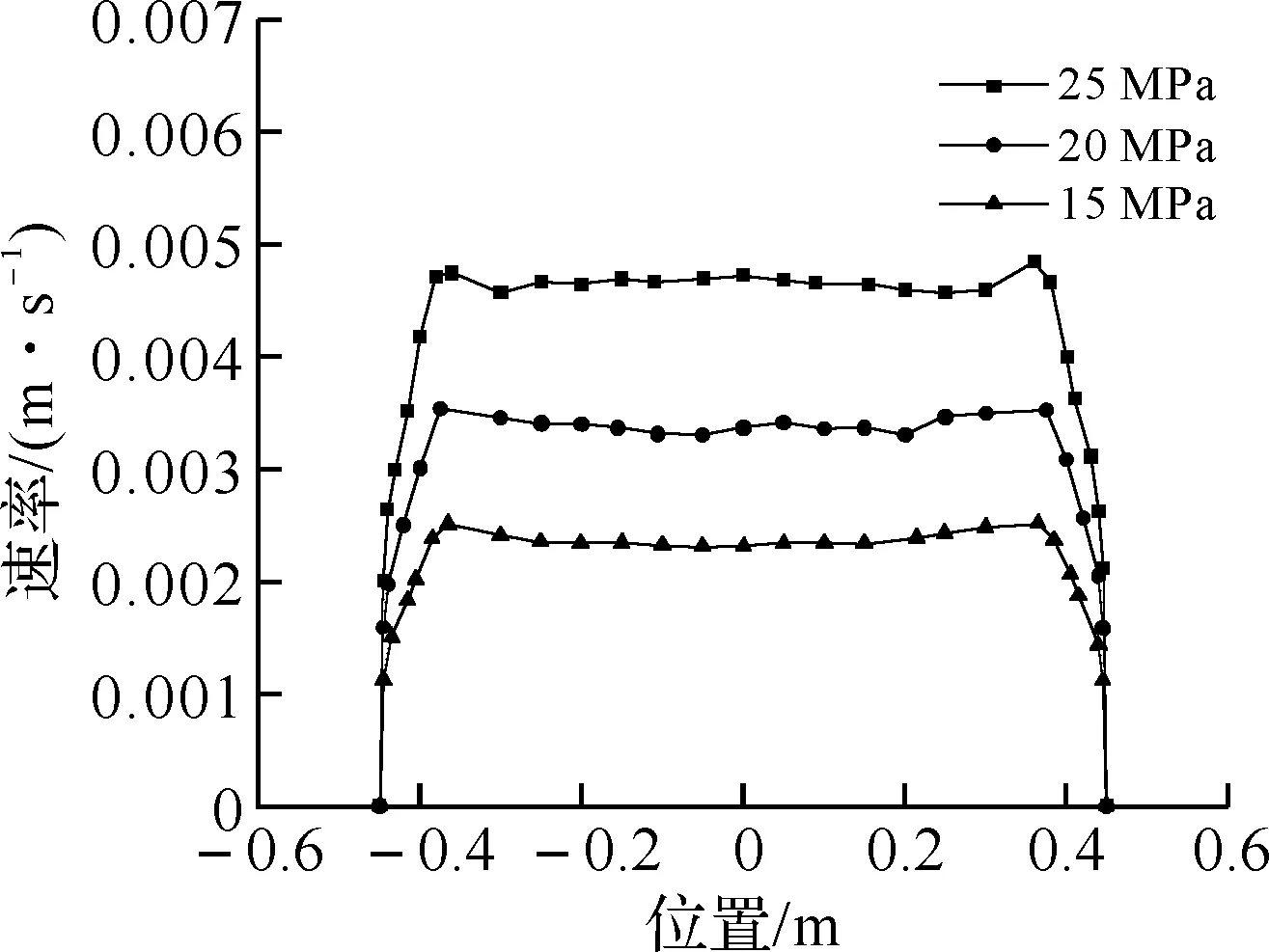
图3 挤出流道出口PVC速率曲线

流道出口速率相对偏差和动量微分方程[7]的公式分别为:

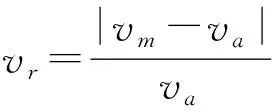
(2)

(3)

式中:ρ为物料密度,kg·m-3;τ为剪切应力张量,Pa;p为压力,Pa;v为速度,m·s-1;vr为速率相对偏差,m·s-1;va为平均速率,mv·s-1;vm为最大或最小速率,m·s-1.

由动量微分方程[6]分析可知,随着流道入口压力的增加,PVC流体出口速率增加;同时,因流道中间部分增加的压力比两端多,使流道出口中部速率比两端增加地多;同时,工业生产中要求速率相对偏差小于2.5%,否则会造成片材出口不均和中间易变形,从而影响产品的质量.

3.2挤出温度对流道出口NR流体速率的影响调节挤出温度能够控制流体的速率.图4为在其他工况相同情况下,不同挤出温度对应流道出口NR流体的速率曲线.由图可知,随着挤出温度的增加,NR流体出口速率曲线上升;同时,流体速率相对偏差均小于2.5%,且没有变化.由自由体积理论分析可知,随着挤出温度升高,NR流体分子间的空穴增加,从而流体受到的流动阻力减小,单元能量增加,有序化程度减小,表观粘度下降,从而使得流体易于流动;同时,NR流体粘度因温度升高而均匀地下降,从而表现为流体出口速率相对偏差未变化.因此,调节挤出温度不会影响流道出口速率的均匀性,但挤出温度不能超过聚合物的热解温度,否则会出现降解或焦烧现象.

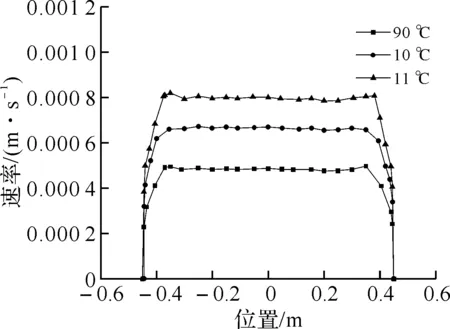
图4 挤出流道出口NR速率曲线

图5 挤出流道出口PS/PP速度矢量图

3.3 PP含量对流道出口PS/PP合金流体速率的影响图5为在其他工况相同情况下不同PP含量对应流道出口PS/PP合金流体的速度矢量图.

由图可知,各出口速度矢量图依次代表PP含量分别为0%、10%和20%时流道出口流体速度矢量图,随着PP含量的增加,聚合物流体的出口速率逐渐上升,且速率相对偏差没有变化.温度与表观粘度得关系式由阿仑尼乌斯公式[8]表示:η=A·exp(Eη/RT)

(4)

式中:Eη为流动活化能,J;η为表观粘度,Pa·s;A为常数;T为绝对温度,K;R为气体常数,8.314 J·mol-1·K-1.

分析可知,挤出温度为180 ℃时,因PS流体的粘度比PP流体高,随着PP含量的增加,使得流体的流动活化能下降,流动性能增加,表观粘度下降,从而使得出口速率升高;同时,PP和PS均匀混合,合金流体的粘度均匀下降,因此流体出口速率相对偏差未变化.采用该方法调节出口速率,在保证该材料特有性能的前提下,能够避免温度调节的局限性,更大范围调节聚合物的出口速率.

表2 优选前后不同工艺参数对应聚合物流体出口速率比

3.4优选聚合物共挤出工艺由以上数值分析可知,共挤出工艺参数直接影响在交汇之前不同聚合物的平均速率比.在当前工艺参数下,NR流体的平均速率与其他聚合物流体相差很远;同时,提高挤出温度容易产生大量热量,从而产生焦烧现象,而入口压力增加过高使得出口速率相对偏差高于2.5%,且不利于节约成本.因此选择其他3种聚合物进行复合比较合理.

图6和图7分别表示优选前和优选后其余3种聚合物流体汇合前流道出口的速度矢量图.

图6 优选前挤出流道出口速度矢量图

图7 优选后挤出流道出口速度矢量图

由图6和图7可知,在聚合物种类和温度选定后,优选其他工艺参数(压力和组分),使得3种聚合物的平均速率比更接近1∶1∶1,且速率相对偏差均小于2.5%;采用优选后的挤出工艺参数,结合实际工况,就能够加快工艺参数调节.

4 结论

以多流道共挤出工艺为研究对象,采用有限元数值方法分析主要工艺参数(挤出温度、入口压力、聚合物种类及合金组成含量)对聚合物流体出口速度场的影响.可知,采用数值分析方法能够在提高效率和节省成本的基础上合理筛选多层复合材料中聚合物的组成,微调其他工艺参数,从而优选共挤出工艺,保证复合材料制品性能和尺寸的稳定性.

参考文献:

[1] 赵艳志,麻向军.塑料挤出成型过程的数值模拟研究[J].橡塑技术与装备,2007,33(4):7-12.

[2] 周国发,纪占国.马鞍型异型材挤出成型过程三维等温粘弹性的数值模拟[J].工程塑料应用,2008,36(8):37-40.

[3] 张敏,孙胜,贾玉玺.双层聚合物共挤出过程的数值模拟[J].高分子材料科学与工程,2005,11:15-18.

[4] 周持兴.聚合物加工理论[M].北京:科学出版社,2004.

[5] 蔡奎,周国发,钟序光,等.气辅共挤成型界面不稳定的数值模拟研究[J].工程塑料应用,2005,33(4):22-25.

[6] 柳和生,涂志刚,熊洪槐.L型异型材挤出口模内聚合物熔体三维等温流动的数值模拟[J].机械设计与制造,2004,10(5):57-60.

[7] 陈晋南,胡敏,彭炯.数值模拟硬质聚氯乙烯双螺杆模具挤出过程[J].科技导报,2009,27(13):54-59.

[8] 何伟,蹇锡高,廖功雄,等.PPEK/PPS共混物流变性能的研究[J].工程塑料应用,2002,8(30):16-19.