TSK模糊逻辑系统混合学习算法的进一步研究

赵 星，郭裕顺

（杭州电子科技大学电子信息学院，浙江杭州310018）

0 引 言

模糊逻辑应用的关键是建立问题的模糊逻辑模型，学习是通过观测数据建立模型的系统方法。BP与最小二乘的混合算法是TSK模糊系统学习的有效算法［1］。这一算法的主要优点是对结论参数用最小二乘可一次求得其全局最优解，从而显著改善学习算法的性能。目前，这是这类模糊系统学习中广泛使用的方法［2、3］。MATLAB的模糊逻辑工具箱也采用了这一算法。本文对这一学习算法作了进一步研究。基本思想是考虑如下事实：既然一个TSK模糊系统前提部分确定后结论部分总可用线性最小二乘法确定，结论中的各参数就可看作是前提部分参数的一个函数，整个模糊逻辑系统可看作是只依赖于前提部分参数的一个系统，学习算法也因此转变为只对前提部分参数的一个优化问题。这降低了优化的参数空间维数，有利于改善算法收敛性能，加快学习速度。对这一问题应用梯度优化，等价于对均方误差目标函数采用一次BP迭代与最小二乘的混合算法，由此还可说明现有混合算法中对前件参数进行多次BP迭代是不必要的。对问题应用拟牛顿优化，可给出TSK模糊系统的拟牛顿学习算法，与直接对全部参数应用拟牛顿优化的算法相比，可显著减少计算量，改善收敛性。对应用其它各种高级优化技术的学习算法，这一观点也是有指导意义的。

1 TSK模糊系统

考虑有n个输入变量，一个输出变量的系统。用模糊逻辑建立这一系统的模型。采用TSK一阶逻辑，规则库是：if x1isμ1 j（x1）and x2isμ2 j（x2）and…and xnisμnj（xn），then y=α0j+α1jx1+…+αnjxn，j=1，2，…，m。取高斯型隶属度函数，对每条规则采用乘积推理机制，则输出是：

对式2作最小化：

式中，yk=y（xk）是在各输入样本点由式1给出的模糊系统输出，e是误差矢量。

将模糊逻辑系统表示为一个前馈网络，则可对式3使用BP算法。但众所周知，BP算法有收敛慢、不稳定、容易陷入局部极小等缺点。

式1中的权重完全由规则的前提决定，y关于结论部分的参数是线性的，可表示为：

根据式 4，把 yk=y（xk）表示为：

式中，d=［d1d2… dN］T。

文献1提出的混合学习算法即是先给定一组规则前提中各变量隶属函数的中心与宽度，由式6的最小二乘解求出一组系数，然后固定这组系数，对各隶属函数的中心与宽度应用BP算法作修改，再从式6解得一组系数，如此交替反复，直至收敛。较基本的BP算法，混合算法的性能有明显改进。

混合算法将式3对全部参数的同时优化分裂为对前提与结论参数的分别优化，实质是一个松弛或交替迭代过程，交替迭代的每一步由对前提参数的BP迭代与对结论参数的最小二乘组成。显然这里存在这样的问题：即对前提参数的BP迭代以多少步为宜？ANFIS只采用一步BP［4］，但没有说明理由。按通常松弛迭代的观点，用多步BP或迭代到收敛，也是合理的。但通过下面的分析可以看出，这是不必要的。

2 只考虑前提参数优化的学习算法

因此可将α看成是各隶属函数的中心与宽度的函数，误差函数式2也成为只取决于中心与宽度的一个函数：

由于α总可由式6的最小二乘解确定：

于是，式3成为：

即对误差函数式8进行优化时，变量只是隶属函数的中心与宽度。与式3比较，式9大大降低了优化的搜索空间维数。显然，降维后对加快收敛速度，改善收敛性能都是有利的。

优化需要计算目标函数的梯度，式8的梯度是：

式中，包含两项导数，分别是由前提决定的与结论参数α对cij的导数。容易求得前一项是：

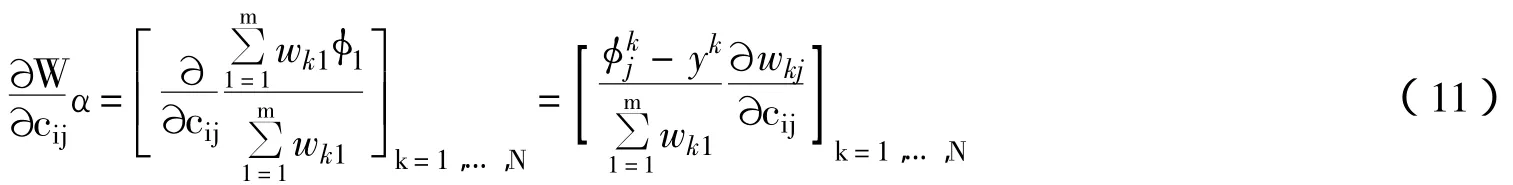
而第二项导数实际并不需要求出，因为当α是式6的最小二乘解时，有：

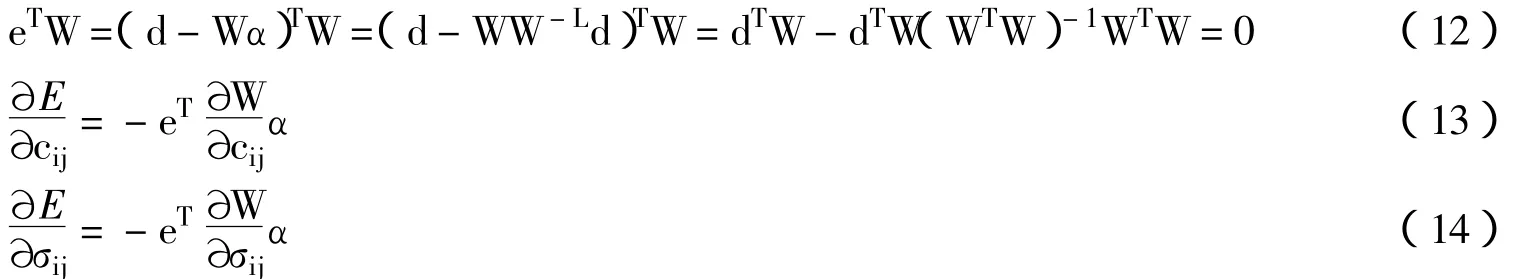
按以上表达计算出梯度，即可对式9进行梯度优化。不难看出式13、14的梯度表达与对式3采用BP算法时需要的梯度是一致的，不同的是式13、14中的α总是由式7决定的。由此可以看出，若采用BP与最小二乘的混合算法并在每次交替迭代中只执行一次BP迭代，则过程与对式9执行一次梯度迭代完全等价（假定采用相同步长）；而执行更多的BP迭代仅仅是在α固定时的一种局部优化，对式3的整体优化则未必有益。

3 采用拟牛顿优化的混合算法

BP算法的收敛速度较慢。拟牛顿法是效果更好的优化技术，将其用于模糊逻辑系统的学习，可取得较快的收敛速度。可直接对式3使用拟牛顿法，如文献5。但通过以上的分析，可知对式9使用拟牛顿法是更为有效的，这就是拟牛顿法与最小二乘混合的学习算法，步骤如下：

（1）按DFP或 BFGS公式确定近似Hessian矩阵H（k）；

（2）在方向 s（k）=-H（k）g（k）上进行一维搜索（g（k）是由式 13、14 组成的梯度矢量），确定前提参数；

（3）用最小二乘确定结论参数；

（4）重复step 1-step 3至收敛。

注意在step 2中执行一维搜索时，每次计算目标函数的值均须根据当时的前提参数用最小二乘求出结论参数，再计算误差的均方和。

上述过程是对式9的拟牛顿迭代。与直接对式3的拟牛顿法相比，这样做显著缩小了Hessian矩阵的规模，减少了计算量；同时由于优化搜索空间维数降低，对收敛可能更有利。

对这一算法进行了数值实验。实验选取了一些数学函数，部分结果如下：

（1）3 输入函数 t=（1+x0.5+y-1+z1.5）2，其中 x，y，z∈［1，6］。利用数论网格法［6］产生 216 个训练样本，再随机产生125个测试样本；

（2）6输入函数y=x1+x0.52+x3x4+2e2（x5-x6），其中x1，x2∈［1，5］，x3∈［0，4］，x4∈［0，0.6］，x5∈［0，1］，x6∈［0，1.2］。随机产生300个训练样本，再利用数论网格法产生2 129个测试样本。

3输入函数是模糊逻辑文献中常见的一个测试例子，6输入函数取自最近的文献7。分别用上述拟牛顿与最小二乘混合的学习算法和MATLAB模糊工具箱中的ANFIS进行训练，结果如表1所示，其中训练时间是在酷睿2上测得的CPU时间，均方误差指在全部检验样本上的均方误差。可以看出较ANFIS，拟牛顿与最小二乘混合的学习算法无论在速度还是精度方面都有明显优势。

表1 建模结果比较

对TSK模糊逻辑系统的学习应用其余各种高级优化技术，如进化算法等，也可按上述类似步骤：每对前提参数迭代一次，即用最小二乘更新一次结论参数，这样每次迭代都等价于系统对全部参数的一次整体优化，而搜索只在由前提参数决定的空间中进行。

4 结 论

本文对TSK模糊逻辑系统的学习算法作了进一步研究。根据这类系统的特点，首先指出学习可转化成只对前提参数的优化，这降低了问题的维数。然后证明采用一次BP迭代与最小二乘的混合算法等价于对这一问题的梯度优化，指出在混合算法中采用多次BP迭代是不必要的。给出了拟牛顿与最小二乘混合的学习算法步骤，并用数值实例说明了效果。本文的观点与结论对采用各种高级优化技术的学习算法也是有指导意义的。

［1］ Jang JS.ANFIS：Aadptive-network-based fuzzy inference system［J］.IEEE Trans SystMan Cybern，1993，23（1）：665-685.

［2］ Chen-Sen Ouyang，Wan-Jui Lee，Shie-Jue Lee.A TSK-type neurofuzzy network approach to system modeling problems［J］.IEEE Trans on SystMan Cybern B，2005，35（4）：751-767.

［3］ Gang Leng.Design for self-organizing fuzzy neural networks based on genetic algorithms［J］.IEEE Trans Fuzzy Syst，2006，14（6）：755-766.

［4］ Jang JS，Sun C T.Neuro-fuzzy modeling and control［J］.Proceedings of the IEEE，1995，83（3）：378-405.

［5］ 张良杰，李衍达，陈惠民.基于变尺度寻优与遗传搜索技术的模糊神经网络全局学习算法［J］.电子学报，1996，24（11）：6-11.

［6］ 方开泰，王元.数论方法在统计中的应用［M］.北京：科学出版社，1996：19-25.

［7］ Botzheim J，Lughofer E，Klement E P，et al.Separated antecedent and consequent learning for Takagi-Sugeno fuzzy system［C］.Canada：IEEE Int Conf on Fuzzy Systems，2006：2 263-2 267.