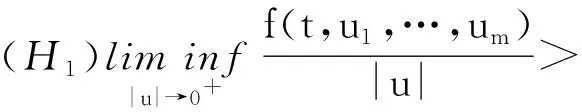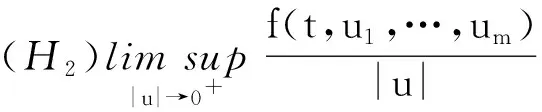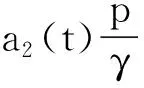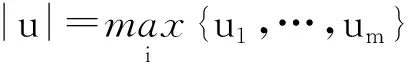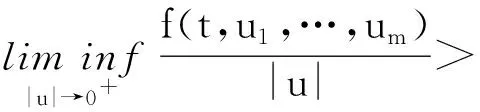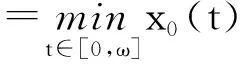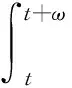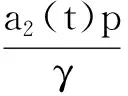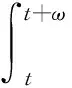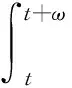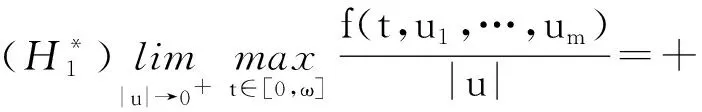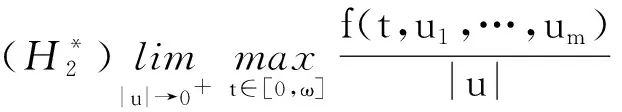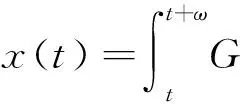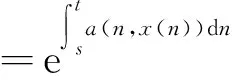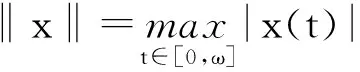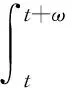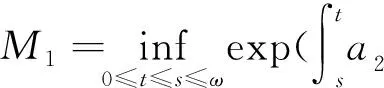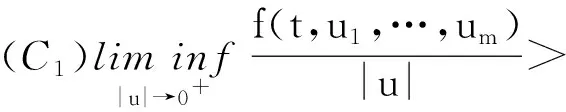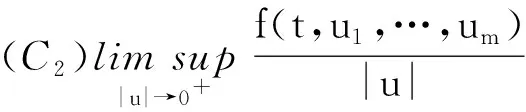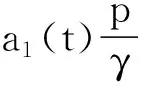具状态依赖时滞更一般微分方程周期正解
2010-11-26丘冠英
丘冠英
(嘉应学院 数学系,广东 梅州 514015)
在文献[1]中,利用Mawhin重合度理论研究了方程具状态依赖时滞方程:x′(t)=-F(t,x(t-τ(t,x(t))))周期正解的存在性,而文献[2]中研究了一类较之更为一般的方程:
x′(t)=-a(t)x(t)+f(t,x(t-τ1(t,x(t))),…,x(t-τm(t,x(t))))
(1)
x′(t)=a(t)x(t)-f(t,x(t-τ1(t,x(t))),…,x(t-τm(t,x(t))))
(2)
至少存在一个周期正解的充分条件.实际上,通过在一个函数空间构造一个全连续算子,再利用不动点定理,它有至少存在两个周期正解和一些保证该类方程存在多个周期正解更好的充分条件.
上述a∈C(R×R+,R),对∀(t,x)∈R×R+有a(t+w,x)=a(t,x),f∈C(R×[R+]m,R+),f(t+w,x1,x2,…,xm)=f(t,x1,x2,…,xm),τi(t+ω,x)=τi(t,x),i=1,2,…,m,R+=[0,+∞],ω>0是一个常数.

1 一些引理及证明
引入本文将要使用的不动点定理.
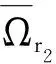
(1)对任意的x∈K∩∂Ωr1和λ∈[0,1]有xλΦx;
(2)存在ψ∈K
则算子Φ在K∩x∈X|r1<|x| 引理2[4]若引理1中的条件(1)和(2)分别用下面的条件来代替, (1)*对任意的x∈K∩∂Ωr2和λ∈[0,1]有xλΦx; (2)*存在ψ∈K 则算子Φ在K∩x∈X|r1<|x| 引理3 x是方程(1)的ω周期解,当且仅当x是下面积分方程的ω周期解. (3) 对上面方程两端从t到t+ω积分,得: 因而x是方程(1)的一个周期解. 反之,若x是方程(3)的一个周期解,则在方程(3)两端同时对t求导,可得方程(1),因而x是方程(1)的周期解,证毕. 下面在Banach空间X中定义算子如下: (Tx)(t),∀t∈R,x∈X. 因而T∶X→X.从上面的分析可知x是方程(1)的ω周期解当且仅当x是算子T在X中的不动点. 引理4T∶K→K. 引理4的证明对于任意的x∈K,t∈R,s∈[t,t+ω],可得: 引理5 T∶K→K是全连续的. 引理5的证明先证明T是连续的.设Ω是K中的任一有界集,则存在数M>0满足对任意的x∈Ω有‖x‖≤M,则由f的连续性和f关于t的周期性可得f(t,u1,…,um)在[0,w]×[0,M]m是一致连续的.因此对于任意的ε>0,存在δ>0满足对任意的t∈R,只要ui,vi∈[0,M]并且|ui-vi|<δ,i=1,2,…,m都有|f(t,u1,…um)-f(t,v1,…,vm)|<ε.在Ω中任意选取一点x0,因为x0(t)在R上连续并且是周期的,所以有x0(t)是一致连续的,因此存在δ1>0(选取δ1>δ),对于满足|t1-t2|<δ1的R中的t1,t2都有: |x0(t1)-x0(t2)|<δ/4 (4) 由于τi(t,y),i=1,2,…,m关于t是周期的,又在R×[0,M]上关于(t,y)是连续的,所以可得τi(t,y),i=1,2,…,m在R×[0,M]上是一致连续的.因此存在数δ2>0(选取δ2<δ1/2)只要满足u1,u2∈[0,M]并且|u1-u2|<δ2,对任意的t∈R都有: |τi(t,u1)-τi(t,u2)|<δ1i=1,2,…,m (5) 因而,由(5)式,对任意的‖x0-y‖<δ2和y∈Ω,都有: |τi(t,x0(t))-τi(t,y0(t))|<δ1, 对任意的t∈R,i=1,2,…,m (6) 因此由(4)—(6)式可得对任意的t∈R,‖x0-y‖<δ2和y∈Ω都有: |x0(t-τi(t,x0(t)))-y(t-τi(t,y(t)))|≤ 从而,对任意的y∈Ω,只要‖x0-y‖<δ2,有: ‖f(t,x0(t-τ1(t,x0(t))),…,x0(t-τm(t,x0(t))))-f(t,y0(t-τ1(t,y0(t))),…,y0(t-τm(t,y0(t))))‖<ε, 对任意的t∈R成立. 所以,若t∈R,y∈Ω并且‖x0-y‖<δ2,则有: 然后,证明集合Tx|x∈Ω中的函数在[0,ω]上是一致有界且等度连续的.因为f(t,u1,…,um)在R×[0,M]m是有界的,所以存在数M3>0满足: ‖f(t,u1,…,um)‖≤M3,对任意的t∈R,ui∈[0,M],i=1,2,…,m (7) 对任意的x∈Ω,有‖x‖≤M,而且 因此可得: (8) 最后,对任意的t∈R,可得: (9) (H4)存在数p>0满足:对任意t∈[0,ω],只要σp≤|u|≤p就有:f(t,u1,…,um)>a1(t)pγ; 定理1 若(A),(H1)和(H3)成立,则方程(1)至少存在两个ω周期正解x1和x2满足0<‖x1‖ f(t,u1,…,um)>γa1(t)(1+ε)|u| (10) 因而,对任意的x∈K且‖x‖=r1,可得r1≥x(t)≥σ‖x‖=σr1>0. 取Ψ≡1.下面证明,对任意的x∈K∩∂Ωr1,η≥0有: x≡Tx+ηΨ (11) 其中Ωr1=x∈X|‖x‖ 用反证法证明.若不然,则∃x0∈K∩∂Ωr1且η0≥0满足: x0=Tx0+η0 (12) 可得α>(1+ε)α.显然矛盾.因此(11)式成立. 接下来,利用假设(H3)的不等式证明对任意的x∈K∩∂Ωp,λ∈[0,1]有: xλTx (13) 其中Ωp={x∈X|‖x‖ 用反证法证明.若不然,则存在x0∈K∩∂Ωp和λ0∈[0,1]使得下面等式成立: x0=λ0Tx0 (14) 显然,λ00,否则有x0≡0,这与x0∈K∩∂Ωp相矛盾,因此对任意的t∈R,有‖x0‖=p且σp≤x0(t)≤p.由(H3)成立,可得对任意的t∈R, (15) 那么由(14)和(15)式,对于任意的t∈R,有: 可得‖x0‖=p 由(11)、(13)式和引理2,可得算子T有不动点x1∈K∩x|r1<‖x‖ (16) 取Ψ≡1.下面证明对任意的x∈K∩∂Ωr2,η≥0有: xTx+ηψ (17) 其中 用反证法证之.若不然,则存在x0∈K∩∂Ωr3和η0≥0满足: x0=Φx0+η0ψ (18) . 所以β≥(1+ε)β.于是,矛盾.因此(17)式成立. 再由(13)、(17)式和引理1,可得算子T有不动点x2∈K∩x|p<‖x‖ 可见,方程(1)至少存在两个ω周期正解,证毕. 显然,由定理1可得下面的推论. 推论1 在定理1中,若条件(A),(H3)保持不变,条件(H1)被下面条件代替: 注记1 定理1得到了比文献[6]的定理2.1更好的结果,理由有二: (1)若在方程(1)中的时滞不是状态依赖的,且方程的右端线性项不含有x,则方程(1)的形式简化为: x′(t)=-a1(t)x(t)+f1(t,x(t-τ1(t)),…,x(t-τm(t))) (19) 这是文献[6]的定理2.1研究的方程.定理1要求的条件(H1)比文献[6]的定理2.1要求的条件要弱,即极限值不需要是+∞. (2)若方程(1)可转化为方程(19)的形式,则函数f1可以不必是恒正的,因而文献[6]的定理2.1的结论不能用在此类方程上. 定理2 假设条件(A),(H2)和(H4)成立,则方程(1)至少存在两个周期正解x1和x2满足0<‖x1‖ 定理2的证明证明方法类似定理1,略. 推论2 若定理2中的条件(A)和(H4)成立,条件(H2)被下面条件代替: 则方程(1)至少有两个ω周期正解. 注记2 定理2得到了比文献[6]的定理2.2更好的结果,理由有二: (1)若在方程(1)中的时滞不是状态依赖的,且方程右端线性项不含有x,则方程(1)的形式简化为 x′(t)=-a1(t)x(t)+f1(t,x(t-τ1(t)),…,x(t-τm(t))) (20) 这是文献[6]的定理2.2研究的方程.定理2要求的条件(H1)比文献[6]的定理2.2要求的条件要弱,即极限值不需要是0. (2)若方程(1)可转化为方程(20)的形式,则函数f1可以不必是恒正的.因而文献[6]的定理2.2的结论不能用在此类方程上. 下面论证方程(2). 同理可得T∶X→X. 取如下假设: (C4)存在数p>0满足:对任意的t∈[0,ω],只要σp≤|u|≤p就有: f(t,u1,…,um)>a2(t)pγ, 则与定理1、定理2的证明过程相同,可得下面定理. 定理3 假设条件(A),(C1)和(C3)成立,则方程(2)至少存在两个ω周期正解x1和x2满足0<‖x1‖ 定理4 假设条件(A),(C2)和(C4)成立,则方程(2)至少存在两个ω周期正解x1和x2满足0<‖x1‖ 参考文献: [1] Li Yongkun,Yang Kuang.Positive solutions in periodic state-dependent delay equations and population models[J].Proceedings of the American Mathematical Society,2001,130(5):1345-1353. [2] 李大潜,林正炎.具状态依赖时滞的微分方程的周期正解[J].高校应用数学学报,2002,17A(1):22-28. [3] Deinling K.Nonlinear functional analysis[M].New York:Springer,1985. [4] Jiang D,O’Regan D,Agarwal R P.Optimal existence theory for single and multiple positive periodic solutions of functional differential equations[J].Nonlinear Oscil,2003,6(3):327-338. [5] 尤秉礼.常微分方程补充教程[M].北京:人民教育出版社,1981:2-3. [6] Li Bing.Positive periodic solution for a nonautonomons delay differential equations[J].ACTA Mathematical Applicata Sinica,2003,19(2):307-316.
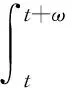
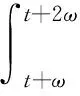
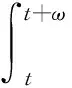
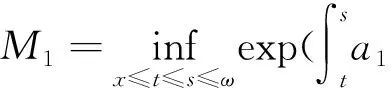
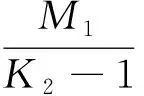
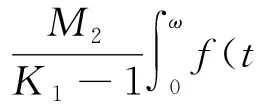

|x0(t-τi(t,x0(t)))-x0(t-τi(t,y(t)))|+|x0(t-τi(t,y(t)))-y(t-τi(t,y(t)))|≤
δ/4+δ2<δ/4+δ/2<δ,i=1,2,…,m.
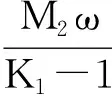
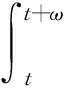
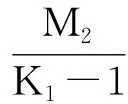
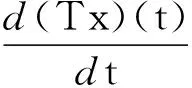
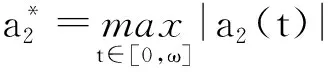
2 多个周期正解的存在性