含有2个最大度点的树的极大独立集个数*
2010-11-24刘雪姿梁小影卜月华
刘雪姿, 梁小影, 卜月华
(浙江师范大学 数理与信息工程学院,浙江 金华 321004)
含有2个最大度点的树的极大独立集个数*
刘雪姿, 梁小影, 卜月华
(浙江师范大学 数理与信息工程学院,浙江 金华 321004)
研究了限制条件下图的极大独立集的计数问题.运用数学归纳法,给出了含有2个最大度点的树的极大独立集个数的最大值,同时刻画了取得最大值时的树.
极大独立集;树;最大度;计数
0 引 言
给定图G,V(G)的一个子集S称为独立集,若S中的任何2个顶点在V(G)中都不相邻;如果一个独立集不真包含于其他任一独立集,就称该独立集为极大独立集;用mi(G)表示G中极大独立集的个数.
图的极大独立集的计数问题对于算法设计有重要的意义.Moon和Moser[1]解决了n阶图G中mi(G)的最大值,以及何时达到最大值的问题;随后,学者们针对这个问题,对许多特殊图进行了研究[2-7].笔者研究了含有2个最大度点的树的极大独立集的个数问题,得到了最大值,并刻画了极图的情况.
1 引 理
引理1[4]对G中的任一顶点x,有
(1)mi(G)≤mi(G-x)+mi(G-N[x]);
(2)如果x是与y相邻的叶子点,那么mi(G)=mi(G-N[x])+mi(G-N[y]).
引理2[4]对任何2个不相交的图G和H,mi(G∪H)=mi(G)mi(H).
明显地,有引理3成立.
引理3设G是一个n阶的图,如果G含有2个顶点x和y,其中d(x)=d(y)=1,N(x)=N(y),那么mi(G)=mi(G-x).
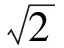

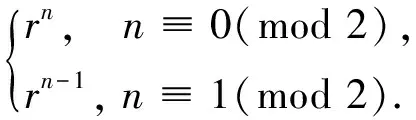
引理4[6]如果T是一棵n阶的树,那么mi(G)≤t1(n),等号成立当且仅当
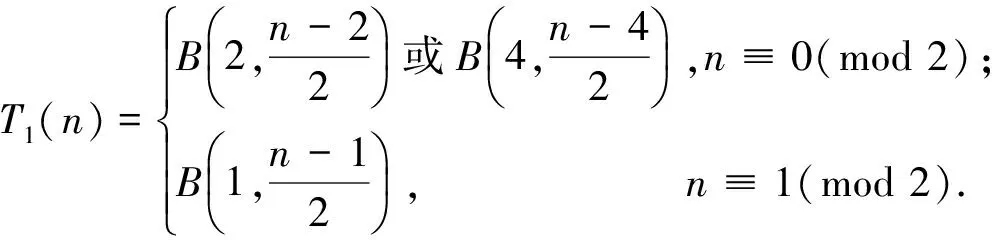
引理5[8]如果F是一个n(n≥1)阶的森林,那么mi(F)≤f(n),等号成立当且仅当
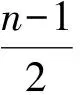
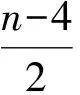
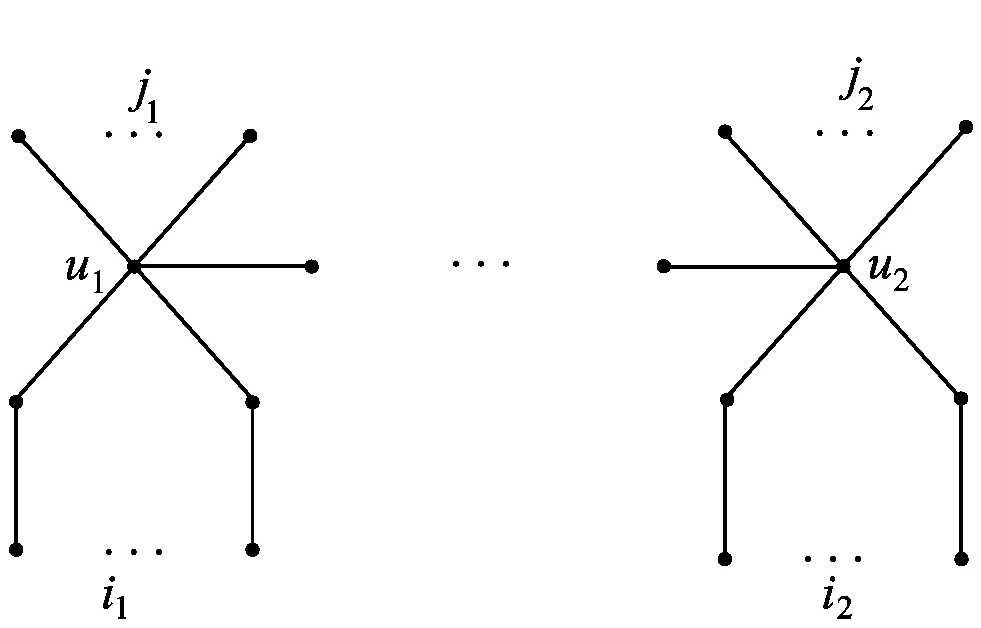
图1 树B(l;i1,j1;i2,j2)
引理6[9]如果T是一棵n阶的树,TT1(n),那么mi(T)≤t2(n),并且等式成立当且仅当T≅T2(n).
B(l;i1,j1;i2,j2)(如图1所示)表示一棵树:给定一条有l个顶点的路P,在路P的一个端点u1下挂有i1条长为2的路和j1条长为1的路,另一个端点u2下挂有i2条长为2的路和j2条长为1的路.当j1=0且j2=0时,把B(l;i1,j1;i2,j2)简记为B(l;i1;i2).
利用引理1易得引理7和引理8.
引理7若l≥2,i1≥1,j1≥1,则
mi(B(l;i1+1,j1-1;i2,j2))≥mi(B(l+1;i1,j1;i2,j2)),
等号成立当且仅当l=2,i2=0,j2=0.
引理8若l≥1,d≥1,则
mi(B(4l+1;d+1;d+1))gt;mi(B(4l+5;d;d));
mi(B(4l-1;d+1;d+1))gt;mi(B(4l+3;d;d)).
2 主要结果
定理1若T是一棵含有2个最大度点的树,则
等号成立当且仅当T≅T(n).其中
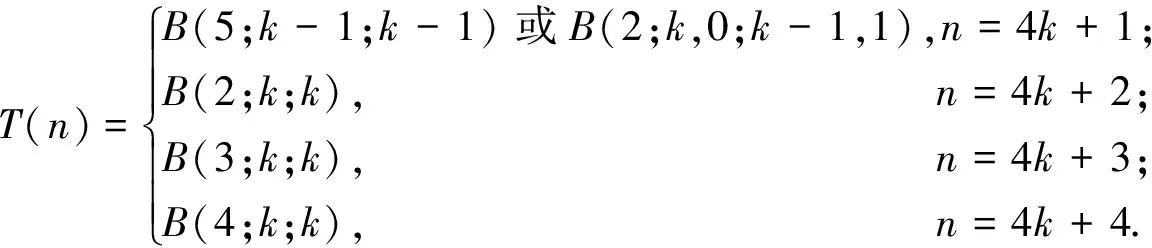
证明 当n=4k+2和n=4k+4时,由引理4知,定理1显然成立,所以只需证明n=4k+1和n=4k+3的情况.对n进行归纳.由于n=4k+3与n=4k+1的证明思路完全类似,因此只证明n=4k+1的情况.
当n≤12时,定理1显然成立.令n≥13,假设当n′lt;n时结论成立.令T为一棵阶为n,且含有2个最大度点的树.为方便起见,令T为平面中的有根树且至少含有2层,w为只有2层子孙的顶点,y为w的一个儿子,x为y的儿子.显然,x是T中的一个叶子点.令n=4k+1.
若d(y)≥3,则

情形1d(w)≠Δ
如果w有1个叶子儿子,由归纳假设可得

假设T′≅T1(n-2d(w)+1),那么T′为图2中的一棵树.不失一般性, 假设a,b,c,d,e,f,g中的一个是w的父亲.显然
mi(T-N[y])=r2(d(w)-2)(rn-2d(w)+1-2+1)=rn-5+r2(d(w)-2).
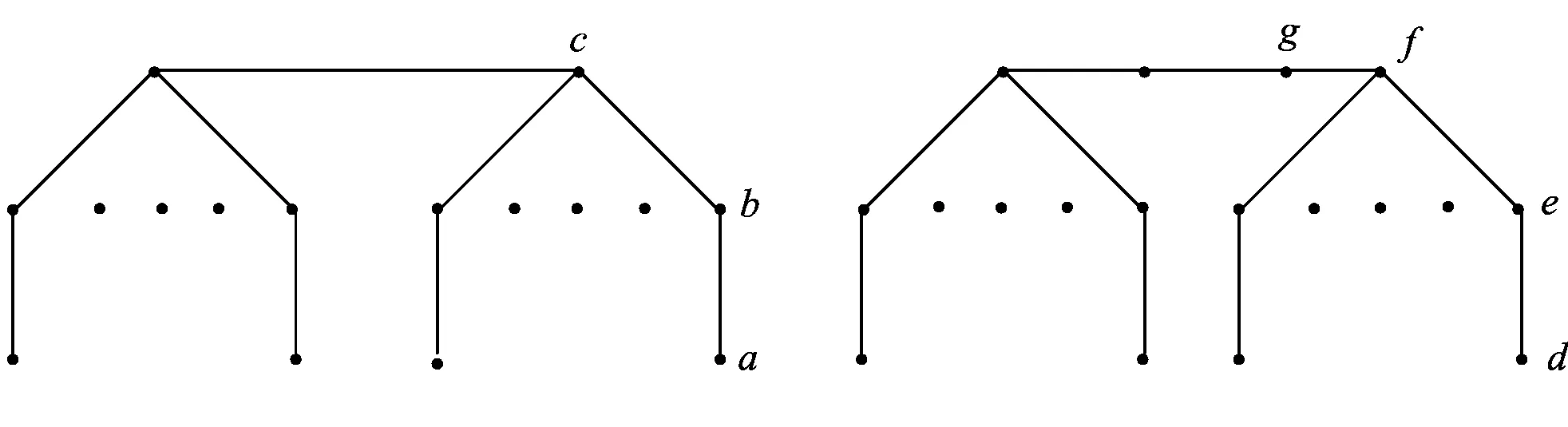
图2 树T′ 的可能情形
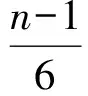
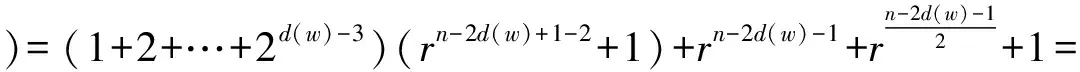

bw∈E(T);cw∈E(T);dw∈E(T);ew∈E(T);fw∈E(T);gw∈E(T).
若T′T(n-2d(w)+1),由归纳假设及引理6有
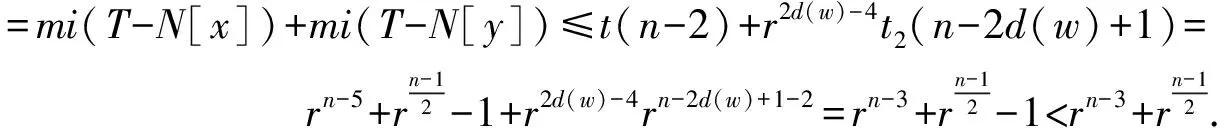
不失一般性,假设只含有2层子孙的顶点是T中的最大度点.
令另外一个最大度点为w′,可以假设w′的不包含w的子孙分支恰好有2层.令P为T中唯一的w-w′路.
(1)P中有1个内点的度至少为3
令z为P中一个度至少为3的内点.由于T中包含2个最大度点,因此d(z)≠Δ.令T以z为根(如图3所示),用A表示T-z中不包含w和w′的分支的点集.由情形1知,A中的任何一个点至多含有1层子孙.因此,z与A中的任何一个点的距离至多为2.分别用T(w)和T(w′)表示T-z中包含w和w′的分支.令|T(w)|=n1, |T(w′)|=n2.

图3 以z 为根的树T
假设z没有叶子儿子,那么n1+n2=n-2d(z)+3.令a为A中的一个叶子点,由归纳假设及引理1有
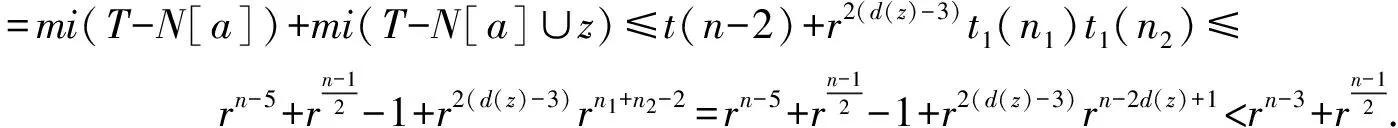
若d(z)≥4,即z中除了x的子孙形成一个匹配.令a为A-x中的一个叶子点,由归纳假设及引理1有
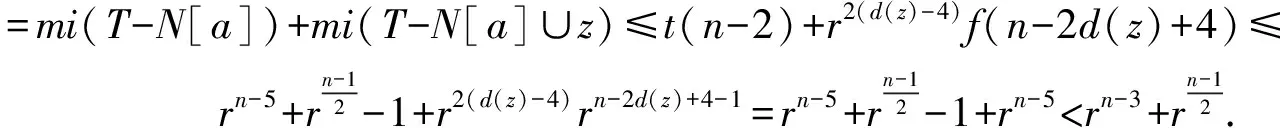
①zw∉E(T)
由引理1及引理4可得
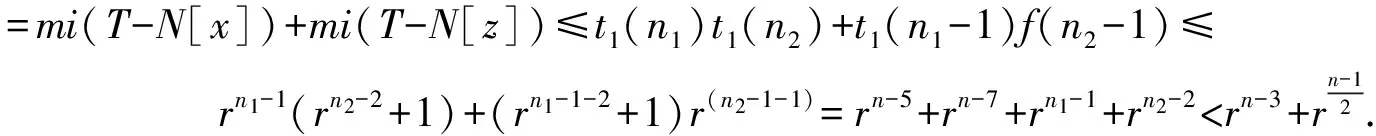
因为n≥13,d(w)=d(w′),所以n1lt;n-6.若w有1个叶子儿子,则由|T(w)|=n1≡1(mod 2)可得w至少含有2个叶子儿子.由引理1及引理4得

此时T≅B(l;i1,j1;i2,j2),其中l+2i1+2i2+j1+j2=4k+1,i1+j1=i2+j2.
①l-2lt;j1+j2
由引理7得,mi(T)≤mi(B(2;i1+j1,0;i2+(l-2-j1),j1+j2-(l-2))).

②l-2≥j1+j2
由引理7得,mi(T)≤mi(B(l-(j1+j2);i1+j1;i2+j2)).
由于l+2i1+2i2+j1+j2=4k+1,i1+j1=i2+j2,所以
(l-2)-(j1+j2)=4k-1-4(i1+j1)=4[k-(i1+j1)]-1≥0.
令k-(i1+j1)=t,t≥1,则l-(j1+j2)=4t+1,t≥1.由引理8可得
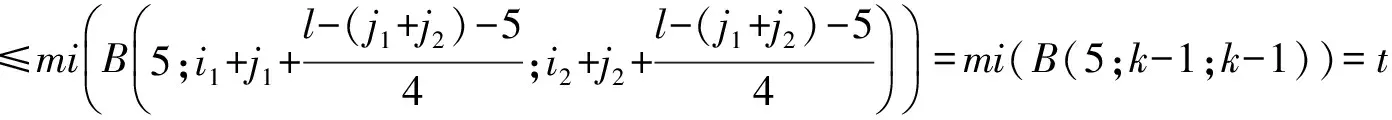
等号成立当且仅当T≅B(5;k-1;k-1).定理1得证.
[1]Moon J W,Moser L.On cliques in graphs[J].Israel J Math,1965,3(1):23-28.
[2]Füredi Z.The number of maximal independent sets in connected graphs[J].J Graph Theory,1987,11(4):463-470.
[3]Griggs J R,Grinstead C M,Guichard D R.The number of maximal independent sets in a connected graph[J].Discrete Math,1988,68(2/3):211-220.
[4]Hujter M,Tuza Z.The number of maximal independent sets in triangle-free graphs[J].SIAM J Discrete Math,1993,6(2):284-288.
[5]Meir A,Moon J W.On maximal independent sets of nodes in trees[J].J Graph Theory,1988,12(2):265-283.
[6]Sagan B E.A note on independent sets in trees[J].SIAM J Discrete Math,1988,1(1):105-108.
[7]Wilf H S.The number of maximal independent sets in a tree[J].SIAM J Algebraic Discrete Methods,1986,7(1):125-130.
[8]Jou M J.The number of maximal independent sets in graphs[D].Taibei:National Center University,1991.
[9]Jou M J,Lina J J.Trees with the second largest number of maximal independent sets[J].Discrete Math,2009,309(13):4469-4474.
(责任编辑 陶立方)
Countingthemaximalindependentsetsintreeswithtwomaximumdegreevertices
LIU Xuezi, LIANG Xiaoying, BU Yuehua
(CollegeofMathematics,PhysicsandInformationEngineering,ZhejiangNormalUniversity,JinhuaZhejiang321004,China)
It was studied the number of maximal independent sets in trees with constrained conditions. Using the mathematical induction, the largest value ofmi(T) for trees with two maximum degree vertices was obtained. Extremal trees achieving these values were also characterized.
maximal independent sets; trees; maximum degree; counting
1001-5051(2010)01-0045-05
2009-05-07
国家自然科学基金资助项目(10701065);浙江省自然科学基金资助项目(Y607467)
刘雪姿(1986-),女,浙江温州人,硕士研究生.研究方向:运筹学与控制论.
O157.5
A
