一类非线性三阶三点边值问题的可解性*

许也平

(杭州广播电视大学,浙江 杭州 310012)

一类非线性三阶三点边值问题的可解性*

许也平

(杭州广播电视大学,浙江 杭州 310012)

讨论了一类非线性项含一阶和二阶导数的三阶三点边值问题的可解性,在非线性项f满足线性增长的限制条件下,通过构造适当的Banach空间,并利用Leray-Schauder非线性抉择,证明了一个存在定理.

三阶三点边值问题；解；存在性；Leray-Schauder非线性抉择

三阶边值问题在应用数学和物理中有着非常重要的意义，对此已有许多研究成果[1-5].本文研究三阶三点边值问题

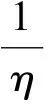
笔者讨论上述非线性项含一阶和二阶导数的三阶三点边值问题(1)解的存在性,得到如下结论：

定理1假设f:[0,1]×R×R×R→R连续并存在非负函数a,b,c,d∈L1[0,1],使得

|f(t,u,v,w)|≤a(t)|u|+b(t)|v|+c(t)|w|+d(t),0≤t≤1.

如果

则问题(1)至少有1个解u*∈C2[0,1].

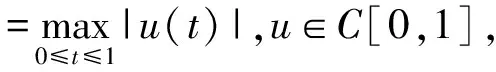
E={u∈C2[0,1]:αu(0)=βu′(0)=0,u′(1)=αu′(η)}

是一个关于范数|‖u‖|=max{‖u‖,‖u′‖,‖u"‖}的Banach空间.

引理1[1]设G(t,s)是齐次三阶三点边值问题

的Green函数，那么

引理2对G(t,s),有

另外,由式(2)知

下面证明

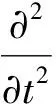
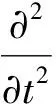
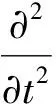
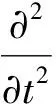
接下来证明

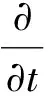
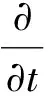
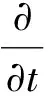
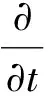
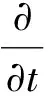
于是引理2得证.

定理1的证明 对于u∈E，定义T算子为

容易证明T:E→E全连续且算子T在E中的不动点均为问题(1)的解.因此,证明的目标就是寻找T在E中的不动点.显然,零函数为问题(1)的解当且仅当

f(t,0,0,0)≡0,0≤t≤1.

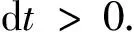
假设存在u∈∂Vρ,λgt;1,使得Tu=λu.因为|‖u‖|=ρ，那么‖u‖≤ρ,‖u′‖≤ρ,‖u"‖≤ρ.这表明

|u(s)|≤ρ,|u′(s)|≤ρ,|u"(s)|≤ρ,0≤s≤1,

故

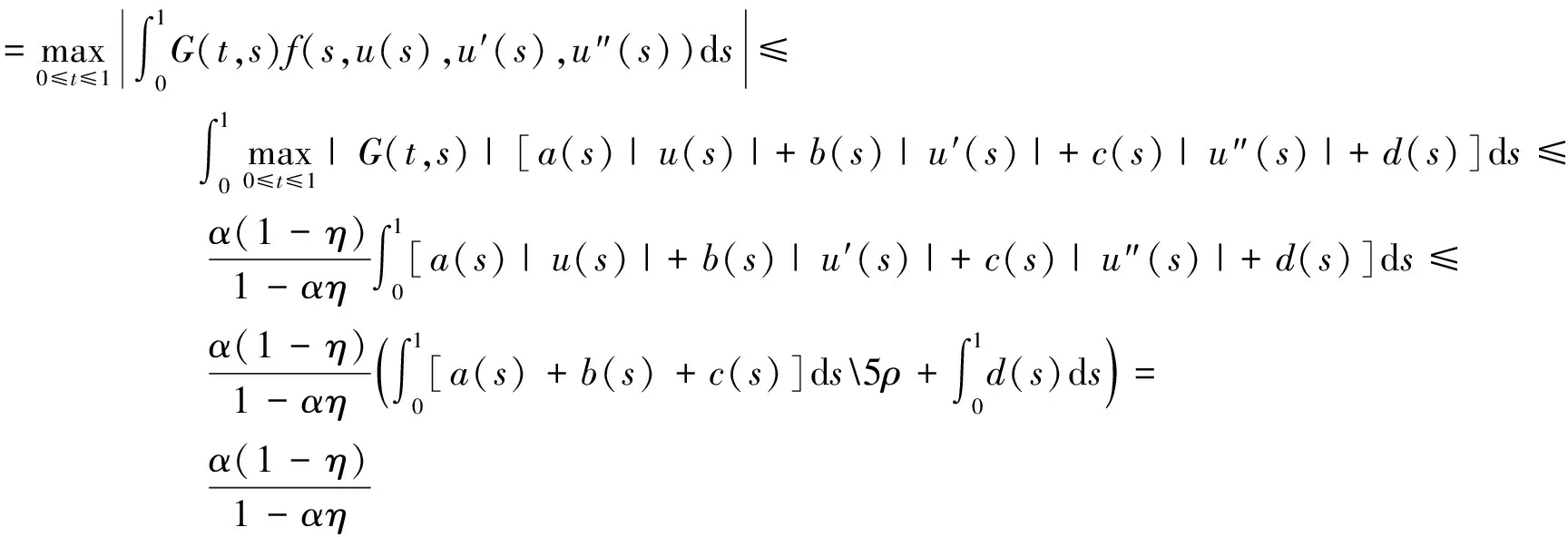
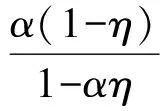
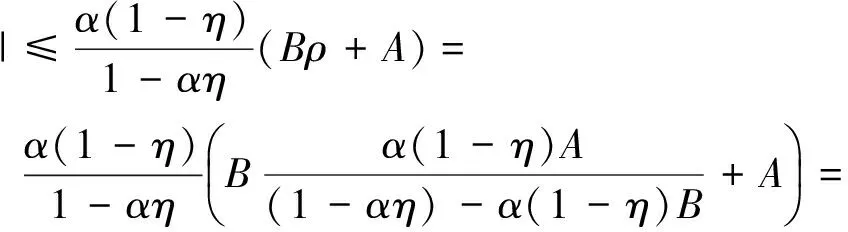
这与λgt;1,ρgt;0矛盾.根据引理3,算子T至少有1个不动点u*∈Vρ.也就是说,问题(1)至少有1个解u*∈E.定理1证毕.

[1]Zhao Weili.Singular perturbations for third order nonlinear boundary value problems[J].Nonl Anal,1994,23(10):1225-1242.

[2]姚庆六.线性增长限制下一类三阶边值问题的可解性[J].纯粹数学与应用数学,2005,21(2):164-167.

[3]王素云.三阶非线性常微分方程正解的存在性[J].甘肃科学学报,2003,15(3):1-5.

[4]Guo Lijun,Sun Jianping,Zhao Yahong.Existence of positive solution for nonlinear third-order three-point boundary value problem[J].Nonlinear Analysis:Theory Methods amp; Applications,2008,68(10):3151-3158.

[5]Yao Qingliu.The existence and multiplicity of positive solutions for a third-order three-point boundary value problem[J].Acta Math Appl Sinica,2003,19(1):117-122.

(责任编辑 陶立方)

Solvabilityofathird-orderthree-pointboundaryvalueproblem

XU Yeping

(HangzhouRadioandTVUniversity,HangzhouZhejiang310012,China)

The solvability was considered for a class of third-order three-point boundary value problem with first and second derivatives. With the nonlinear termfsatisfied a restriction of linear growth, by constructing a suitable Banach space and applying the Leray-Schauder nonlinear alternative, an existence theorem was established.

third-order three-point boundary value problem; solutions; existence; Leray-Schauder nonlinear alternative

1001-5051(2010)01-0022-05

2009-09-06

浙江省教育厅科研项目(Y200804663)

许也平(1962-),男,浙江杭州人，副教授.研究方向:微分方程及其应用.

O175.8

A