平坦模的一些注记*

潘 媛, 陈淼森

(1.浙江师范大学 数理与信息工程学院,浙江 金华 321004;2.义乌工商职业技术学院,浙江 义乌 322000)

平坦模的一些注记*

潘 媛1,2, 陈淼森1

(1.浙江师范大学 数理与信息工程学院,浙江 金华 321004;2.义乌工商职业技术学院,浙江 义乌 322000)

主要讨论了平坦模的一些性质.设R是诺特环,J是R的Jacobson根,证明了R/J是平坦R-模当且仅当R是半单环;若Λ是局部有限的诺特的连通分次代数,M是任意有限生成的分次Λ-模,则M是平坦模当且仅当M是投射模,当且仅当M是自由模.

半单环;连通分次代数;平坦模;投射模;自由模

0 引 言

平坦模是经典模论和同调代数的基本研究对象之一,在数学的诸多领域中有着十分广泛的应用[1-2].随着模理论的不断发展，平坦模的理论也受到越来越多学者的关注，其概念也有不同方向的推广.例如，广义平坦模[3]、强Gorensrein平坦模[4]以及在复形上研究平坦模的性质[5]，等等.本文主要讨论了平坦模的一些性质,利用平坦模刻画半单环.设R是诺特环,J是R的Jacobson根,证明了R/J是平坦R-模当且仅当R是半单环.然而，半单环上的每个模都是投射模,这就会自然地考虑如何用平坦模去刻画投射模和自由模这一问题,从而得到了:若Λ是局部有限的诺特的连通分次代数,M是任意有限生成的分次Λ-模,则M是平坦模当且仅当M是投射模，当且仅当M是自由模.

1 平坦模对半单环的刻画

半单环是经典环论中结构最清楚、性质最好的一类环,且有性质：R是半单环当且仅当任意R-模是投射模.

证明 由于K⊗R/I≅K/KI,M⊗R/I≅M/MI,则0→K⊗R/I→M⊗R/I是正合的当且仅当f:K/KI→M/MI,x+KI|→x+MI是单同态.对任意的x∈K∩M,kerf=0当且仅当若k∈MI,则k∈KI,即KI≥K∩MI.显然有KI≤K∩MI,因此KI=K∩MI.

引理2设J为环R的Jacobson根,则下列陈述等价:

(1)R/J是平坦R-模;

(2)R的任意右理想I都有IJ=I∩J;

(3)R的任意右理想I,TorR1(R/I,R/J)=0.

证明 (1)⟹(2) 若R/J是平坦模,则对R的任意右理想I,有正合列0→I⊗R/J→R⊗R/J,由引理1得IJ=I∩RJ=I∩J.

(2)⟹(1) 设I是R的任意一个右理想,则根据引理1可知,0→I⊗RR/J→R⊗RR/J是正合的,故R/J是平坦右R-模.

(1)⟸⟹(3) 设I是R的任意一个右理想,则有正合列0→I→R→R/I→0.由长正合列定理得

…→TorR1(R/I,R/J)→R/I⊗RI→R/I⊗RR→R/I⊗R/J→0,

故TorR1(R/I,R/J)=IJ/I∩J.因此,TorR1(R/I,R/J)=0当且仅当IJ=I∩J.

引理3(Nakayama引理)[1]设I是环R的左理想,I≤J,M是有限生成左R-模,若IM=M,则M=0.

由引理3,可考虑R/J的平坦性,并且用其平坦性来刻画半单环.

定理1设R是诺特环,J为R的Jacobson根,则下列陈述等价:

(1)R/J是平坦R-模;

(2)R/J是投射R-模;

(3)R是半单环.

证明 (1)⟹(3) 设R/J是平坦模,由引理2知,对任意的右理想I,都有IJ=I∩J.取I=J,得J2=J.注意到R是诺特环,故有限生成模的子模还是有限生成的.又正则模R是有限生成的,由引理3得J=0.故R是半单的.

推论1设R是诺特环,若J≠0,则R/J不可能是平坦模.

2 平坦模、投射模和自由模之间的关系

平坦模、投射模和自由模构成了模论中最基本、最重要的三大模类,且有以下关系:

M是自由模⟹M是投射模⟹M是平坦模.

因此，自然要考虑的一个问题是:平坦模何时成为投射模,投射模何时是自由模?

在接下来的讨论中，用R表示一个有单位元的诺特环；在没有特别说明时,Λ均为局部有限的诺特连通分次代数;并用Mod(Λ)和Grmod(Λ)表示Λ-模范畴和分次Λ-模范畴;mod(Λ)和grmod(Λ)表示有限生成的Λ-模范畴和有限生成的分次Λ-模范畴,易知mod(Λ)和grmod(Λ)分别是Mod(Λ)和Grmod(Λ)的满子范畴;用r表示Λ的分次Jacobson根.对一个局部有限的诺特连通分次代数Λ来说(即形如Λ=k⊕Λ1⊕Λ2⊕…⊕Λn⊕…,且满足:(1)Λ是诺特的(未必是有限维);(2)每个向量空间Λi都是有限维的;(3)k是任意一个基础域),有如下主要结果:

定理2设Λ=k⊕Λ1⊕Λ2⊕…⊕Λn⊕…是一个局部有限的诺特的连通分次代数,M是有限生成的Λ-模,则下列陈述等价:

(1)M是平坦模;

(2)M是投射模;

(3)M是自由模.

证明 (3)⟹(2)和(2)⟹(1)显然，故略.下面只证(1)⟹(3).分几步来证明:

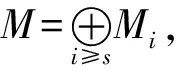
第2步:对于任意一个有限生成的分次Λ-模M,证明存在一个有限维的向量空间Mc,使得φ:Λ⊗kMc→M是grmod(Λ)中的满同态.特别地,诱导态射1⊗Λφ:k⊗ΛΛ⊗kMc→k⊗ΛM是同构的.事实上,作为一个分次向量空间,M=rM⊕Mc,其中Mc是rM在M中的直和补.不难发现,Mc就是M作为Λ-分次模,且以其极小生成齐次元作为基生成的向量空间.考虑到M是有限生成的,故Mc是有限维的.作映射

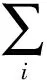
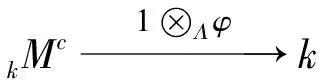
由于k⊗ΛΛ⊗kMc≅Mc及k⊗ΛM≅Mc作为向量空间是有限维的,故1⊗Λφ是同构的.

第3步:证明M是自由的当且仅当TorΛ1(k,k)=0,其中M∈grmod(Λ).根据第2步可得正合列

0→kerφ→Λ⊗kMc→M→0.

由文献[2]中的长正合列定理知,有正合列

…→TorΛ1(k,k)→k⊗Λkerφ→k⊗ΛΛ⊗kMc→k⊗ΛM→0.

假设TorΛ1(k,k)=0,则有正合列

0→k⊗Λkerφ→k⊗ΛΛ⊗kMc→k⊗ΛM→0.

根据第2步知,k⊗Λkerφ=0;再根据第1步知,kerφ=0.所以,M≅Λ⊗kMc是自由的.必要性是显然的，故略.

因此，若M是平坦模,则TorΛ≥1(k,k)=0,由第3步知,M是自由模.

综上，定理2证毕.

[1]Anderson F W,Fuller K R.Rings and Categories of Modules[M].New York:Springer-Verlag,1974:169;177-249.

[2]Weibel C A.An Introduction to Homological Algebra[M].Cambridge:Cambridge University Press,1995:66-90.

[3]Crivei S.Epic Envelopes by Generalized Flat Modules[J].Mathematica(Cluj),2009,51(1):47-53.

[4]Ding Nanqing,Li Yuanlin,Mao Lixin.Strongly Gorenstein Flat Modules[J].J Aust Math Soc,2009,86(3):323-338.

[5]Hashimoto M.Acyclicity of Complexes of Flat Modules[J].Nagoya Math J,2008,192:111-118.

(责任编辑 陶立方)

Somenotesonflatmodules

PAN Yuan1,2, CHEN Miaosen1

(1.CollegeofMathematics,PhysicsandInformationEngineering,ZhejiangNormalUniversity,JinhuaZhejiang321004,China; 2.YiwuIndustrialandCommercialCollege,YiwuZhejiang322000,China)

Some new properties of modules were discussed. LetRbe a Noetherian ring andJdenote its Jacobson radical, it was proved thatR/Jwould be flat if and only ifRwas supposed to be semi-simple. LetΛbe a Noetherian locally finite graded algebra andMa finitely generated graded module overΛ, thenMwould be flat if and only ifMwas supposed to be projective or free.

semisimple rings; connected graded algebra; flat modules; projective modules; free modules

1001-5051(2010)01-0038-03

2009-11-06

潘 媛(1980-),女,湖北广水人,讲师,硕士研究生.研究方向：非交换代数.

O153

A