分类讨论 数形结合 解题赏析——2010年浙江省数学高考自选模块解题体验

●

(温岭中学 浙江温岭 318000)

分类讨论数形结合解题赏析——2010年浙江省数学高考自选模块解题体验

●孙海琴

(温岭中学 浙江温岭 318000)

2010年浙江省数学高考自选模块“数学史与不等式选讲”考查的是含参数的绝对值不等式.作为选拔性的题目，含参数的绝对值不等式有一定的难度，需要对参数进行合理地分类讨论，在讨论过程中运算也很复杂.下面给出这道题的其他解法.

题目已知m∈R，解关于x的不等式:

1-x≤|x-m|≤1+x.

1 考生答题反馈

解法1等价变形去绝对值符号.原不等式等价于

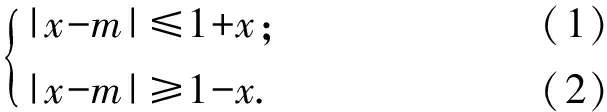
由式(1),得

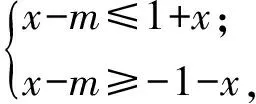
即

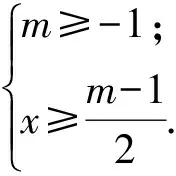
(3)

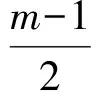
x∈φ.

(4)

由式(2),得

x-m≥1-x或x-m≤x-1,

即

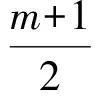
(5)

实际上,式(5)等价于当m≥1时，x∈R；当m<1时，

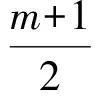
(6)

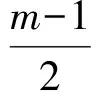
等价变形对大部分学生来说是比较简单的，但对式(3)、式(5)的等价变形是此题的难点.绝大多数学生因为无法理解式(3)和式(5)而无法继续完成此题.原因有2个：一是对变量参数的理解没到位；二是没有真正理解“且”与“或”.

解法2零点分区间讨论去绝对值符号(参考答案的解法,此处略)，此法解题的困难同解法1.

2 巧妙解法

其实对于含参数的绝对值不等式，不应急于去绝对值符号.如果采用数形结合的方法，那么不仅可以大大降低难度，而且可以变抽象为直观，有利于学生理解.

解法3利用数形结合,分别作出函数y=1-x，y=|x-m|，y=1+x的图像，则不等式1-x≤|x-m|≤1+x表示介于直线y=1+x下方和直线y=1-x上方之间.

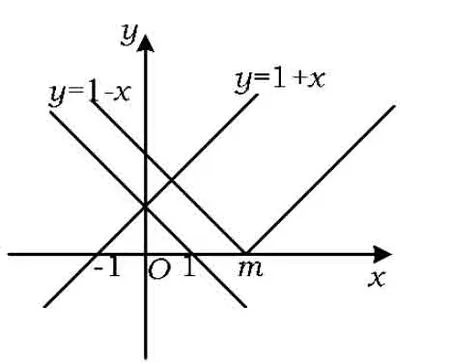
图1

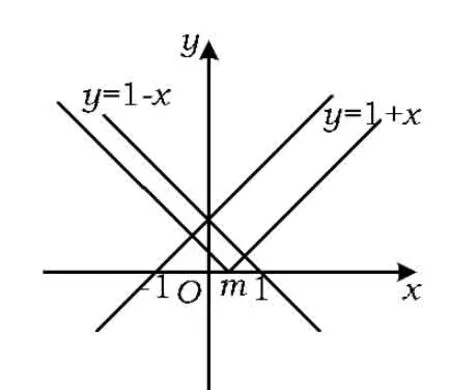
图2

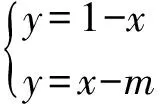
当m<-1时，不等式的解集为φ，如图3所示.

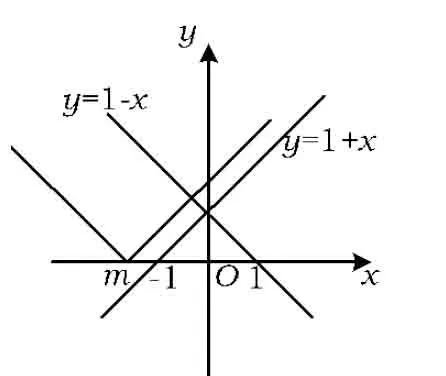
图3

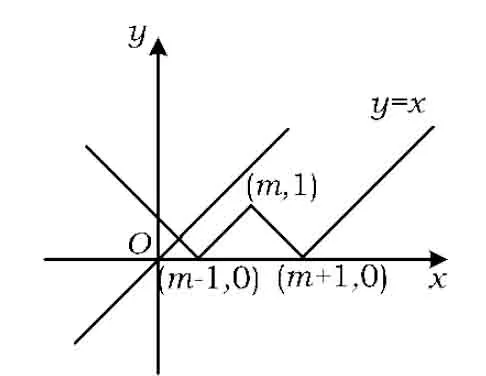
图4

解法4利用数形结合,不等式1-x≤|x-m|≤1+x等价于

-x≤|x-m|-1≤x，

即

||x-m|-1|≤x，

于是作出函数y=||x-m|-1|和函数y=x的图像.

当m-1≥0，即m≥1时，由

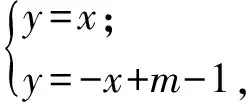
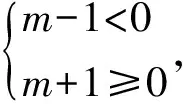
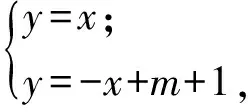
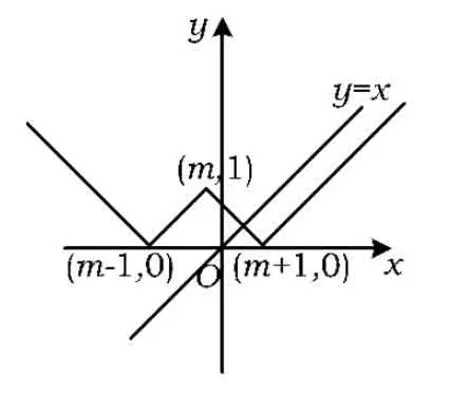
图5

图6

数形结合的方法其优势是让讨论变得自然，让分类标准明确，答案简洁明了.其局限性是学生作图能力差，数形结合的意识淡薄，自行处理图像有困难.

3 教学思考与启示

3.1 应加强学生对数学基础知识的学习

从学生不完善的解法中可以发现，出现的问题主要是学生对一些基本概念(譬如交、并)、基本技能(数形结合)没有掌握好.在教学中应强调对基本概念和基本思想的理解和掌握，对一些核心概念和基本思想(如函数、空间观念、运算、数形结合、向量、导数、统计、随机观念、算法等)要贯穿于高中数学教学的始终，帮助学生逐步加深理解.熟练掌握一些基本技能，如重视运算、作图、推理、处理数据以及科学计算器的使用等基本技能训练,但应注意避免过于繁杂和技巧性过强的训练.这些对学好数学都是非常重要的.

3.2 应加强学生对数学知识整体的认识

高中数学课程是以模块和专题的形式呈现的.因此，在教学中应注意沟通各部分内容之间的联系，例如，在教学中要注重函数、方程、不等式的联系；数与形的联系等.通过类比、联想、知识的迁移和应用等方式，使学生体会知识之间的有机联系，感受数学的整体性，进一步理解数学的本质，提高解决问题的能力.