从困惑到解惑 得益于科研先行

●

(江口中学 广东封开 526500)

从困惑到解惑得益于科研先行

●黎伟初

(江口中学 广东封开 526500)

1 困惑点的生成

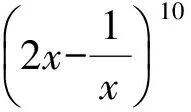
通常的解法是：设展开式中第r+1项的系数绝对值最大.由

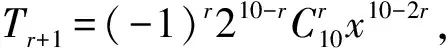
得

即

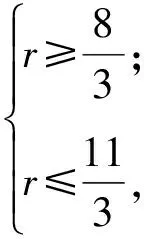
解得

r=3，

故系数绝对值最大的项是T4=-15 360x4.

困惑点1为什么只要第r+1项的系数绝对值与前后相邻两项的系数绝对值一比较就可以求出“系数绝对值最大项”的r值？有什么理论依据？能否拿第r+1项的系数绝对值与其他任意两项的系数绝对值比较也可以确定“系数绝对值最大的项”的值？

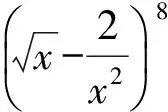
学生的做题情况为：设展开式中第r+1项系数最大.由

得

得

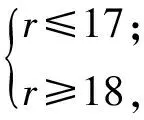
即r值不存在!

解这个组合数不等式确实得到r值不存在的结果.

困惑点2为什么计算出的r值会超出r∈{0,1,2,3,4,5,6,7,8}的范围?

2 解惑的心路历程

这2个困惑点迫使笔者有一个解惑的驱动,下面把科研的心路历程奉献给广大同行,供参考.

历程1对例1来说，拿第r+1项的系数绝对值与任意一项(譬如第2,7项)的系数绝对值相比较，试图求出目标项的r值.由

无法求出r的值,原因是r为抽象值，不等式2边的r约简不了.

历程2拿第r+1项的系数绝对值与跟第r+1项相距离为3,4的项的系数绝对值相比较，试图求出目标项r的值.由不等式组

无法求出r的值,原因是无法求解高次不等式组.

历程3结合历程1和历程2的解法碰壁及例1的系数绝对值最大项是第4项，突获灵感：对任意一个二项式的展开式，系数绝对值最大的项是否都在展开式的中间或偏向中间.不妨把例1展开式所有项的系数绝对值逐一求出验证想法,发现系数绝对值逐渐递增再逐渐递减.

历程4从历程3又生灵感：系数绝对值有没有严格单调递增或严格单调递减，使得“系数绝对值”出现在2端？经冥思苦想，想出一个例子.

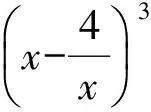
历程5结合历程3与历程4，进一步否定了“系数绝对值最大的项在展开式的中间或偏向中间”的观点，也否定了“系数绝对值最大的项在2端”的观点.展开式中系数绝对值排成一个数列，该数列有什么样的性质？是否具有单调性？若具有单调性并且知道其单调性，则最值项定位基本把握准确.基于这样的想法，继续设一般的二项式探究它的系数绝对值的性质.

例4设二项式(axt+bxs)n或(axt+bys)n(其中s,t∈Q,a,b≠0).

探究因为

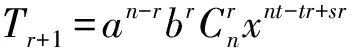
所以第r+1项与第r项的系数绝对值之比为(出于比较相邻两项系数绝对值大小的考量)：

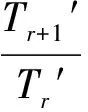
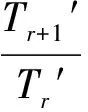
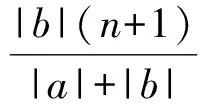
又r∈N*，则

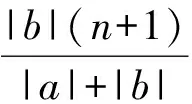
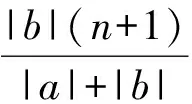
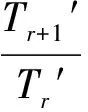
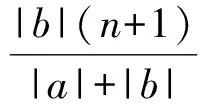
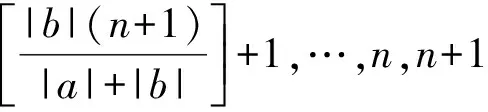
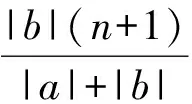
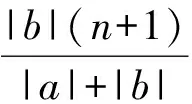
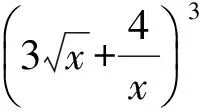
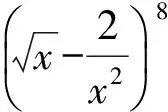
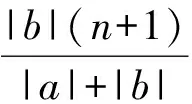
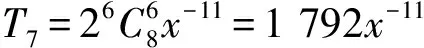
和

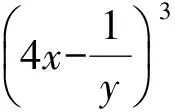
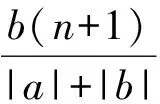
历程7历程5和历程6已经探明了系数绝对值的变化规律，因此对一般的二项式(axt+bxs)n或(axt+bys)n(其中s,t∈Q,a,b≠0)，若展开式中第r+1项的系数绝对值最大，则说明从第1项到第r项(或第r+1项)的系数绝对值构成递增关系，从第r+1项到第n+1项的系数绝对值构成递减关系.这自然有

这就证明了例1解法的理论依据.至此，文章开头所提的困惑点1得到解决，与此同时也找到新的确定展开式中系数绝对值最大项方法的求解公式.对于困惑点2，原因在于所列不等式组

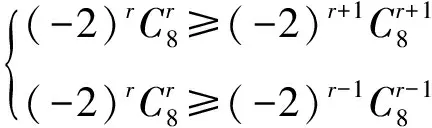
是不完全正确的.细心观察不等式2边的系数，显然有正负系数混杂在一起.正确解法应是设第2k+1项正系数最大，此时r=2k，则

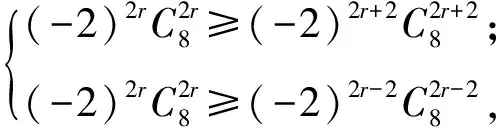
解得r=3，即系数最大项是T7=1 792x-11.至此困惑点2也得到了解决.

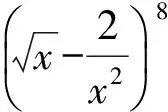
重解因为

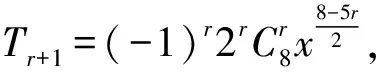
所以设第r+1项系数的绝对值最大，则有不等式组

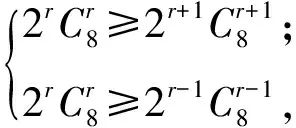
解得

5≤r≤6,

即第6项与第7项系数绝对值最大且相等.又

同理可得

T7=1 792x-11，

比较知系数最大的项应是第7项：T7=1 792x-11.

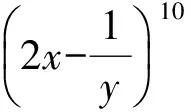
分析因为

设第r+1项系数的绝对值最大，则有不等式组

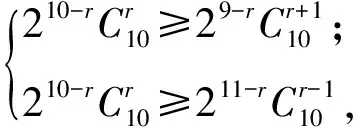
即

得r=3，所以

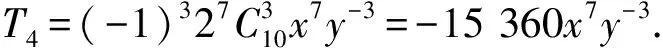
另前后相邻2项分别是

T3=11 520x8y-2和T5=13 440x6y-4，

经比较知,系数最大项是T5=13 440x6y-4.

3 解惑后的收获盘点

由困惑到解惑的心路历程，逐步探明了一些重要结论和方法，对二项式(axt+bxs)n或(axt+bys)n(其中s,t∈Q,a,b≠0)有：

(1)展开式中各项系数的绝对值构成先增后减的数列，或递减数列(当系数绝对值最大在首项时)，或递增数列(当系数绝对值最大在末项时).

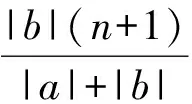
(3)至于要找出系数(当系数有正有负时)最大的项，可分2步：第1步,先确定系数绝对值最大时的值;第2步,再计算Tr+1项的系数与前后2相邻项Tr,Tr+2的系数，比较这3项系数就可确定目标项.

以上为找二项展开式中系数(或绝对值)最大项提供了强有力的操作工具与理论方法，以服务于广大师生.