一个不等式猜想引出的问题

●

(衢州市第二中学 浙江衢州 324000)

一个不等式猜想引出的问题

●舒金根

(衢州市第二中学 浙江衢州 324000)

在文献[1]中,李韵教师提出了如下猜想:

设a,b,c∈R+且a+b+c=1,n∈N+，则

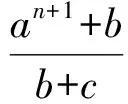
无独有偶，文献[2]～[4]都用极限法和特殊值法指出该猜想是错误的.

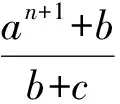
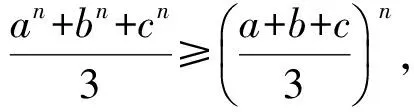
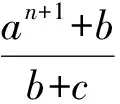
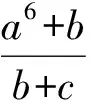
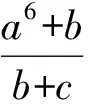
81(a7+b7+c7)+81abc(a5+b5+c5)+81(ab+bc+ca)-41(b2c+c2a+a2b)≥

122(a2c+b2c+c2b+2abc).

(1)

因为

ab+bc+ca=(ab+ca+ca)(a+b+c)=ab2+ac2+ba2+bc2+ca2+cb2+3abc,

所以不等式(1)等价于

81(a7+b7+c7)+81abc(a5+b5+c5)+40(b2c+c2a+a2b)≥41(a2c+b2a+c2b)+abc.

(2)

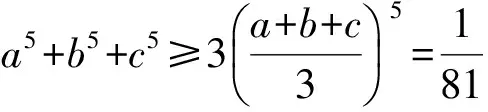
81(a7+b7+c7)+40(b2c+c2a+a2b)-41(a2c+b2a+c2b)≥0，

即

81(a7+b7+c7)+[40(b2c+c2a+a2b)-41(a2c+b2a+c2b)](a+b+c)4≥0.

当a≥b≥c时，设a=1+x+y，b=1+x(x≥0,y≥0)，并代入不等式(3)得

不等式(3)的左边=146x7+x6(974+1 159y)+x5(2 706+6 810y+3 565y2)+x4(3 966+15 513y+

17 649y2+5 043y3)+x3(3 141+16 680y+32 820y2+19 736y3+4 106y4)+

x2(1 134+7 992y+27 630y2+27 156y3+11 793y4+2 060y5)+x(1 134y+

9 909y2+14 916y3+10 515y4+3 870y5+607y6)+1 134y2+2 529y3+2 742y4+

1 686y5+566y6+81y7≥0;

当b≥a≥c时，设b=1+x+y,a=1+x(x≥0,y≥0)，代入不等式(3),得

不等式(3)的左边=146x7+x6(974-137y)+x5(2 706-966y-323y2)+x4(3 966-1 983y-1 791y2+

507y3)+x3(3 141-816y-2 172y2+2 240y3+1 514y4)+x2(1 134+1 431y+

1 386y2+5 286y3+4 989y4+1 331y5)+x(1 134y+3 348y2+6 168y3+6 141y4+

2 898y5+526y6)+1 134y2+2 529y3+2 742y4+1 686y5+566y6+81y7.

(4)

为了判断式(4)的正负,将式(4)恒等变形为

(96x7-137x6y+81y7)+(974x6-966x5y+566y6)+(50x7-323x5y2+1 331x2y5)+(2 706x5-1 983x4y+1 686y5)+x4(3 966-1 791y2+507y3)+x3(3 141-816y-2 172y2+2 240y3+1 514y4)+x2(1 134+1 431y+1 386y2+5 286y3+4 989y4)+x(1 134y+3 348y2+6 168y3+6 141y4+2 898y5+526y6)+1 134y2+2 529y3+2 742y4.

(5)

下证式(5)中每个“括号”均为非负.

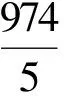
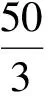
364x5y≥323x5y2;

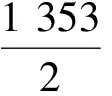
4 533x4y≥1 983x4y;

当0≤y≤1时，

3 141-816y-2 172y2+2 240y3+1 514y4≥3 141-816-2 172>0;

当y>1时，3 141-816y-2 172y2+2 240y3+1 514y4=y2(2 240y-2 172)+y(1 514y3-816)+3 141>0,

即

3 141-816y-2 172y2+2 240y3+1 514y4>0，

从而式(5)≥0.故

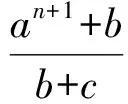
证明设a=0.15,b=0.35,c=0.5,则

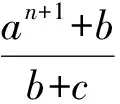
于是

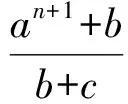
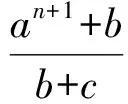
[1] 李韵.优美不等式中的三姐妹[J.]数学通讯,2009(1):37.

[2] 车之森.一个不等式猜想的否定及猜想成立的条件[J].数学通讯，2009(6):33.

[3] 王凯成.一个猜想的探究[J].数学通讯，2009(6):34.

[4] 吴开亮.一个猜想的否定及改正[J].数学通讯，2009(11):33.

[5] 舒金根.一个不等式猜想引发的思考[J].中学数学研究，2010(5):15-16.