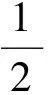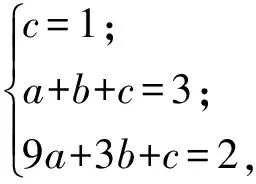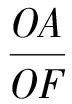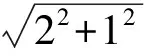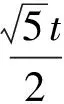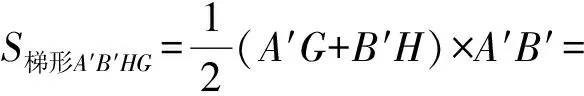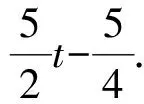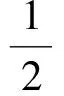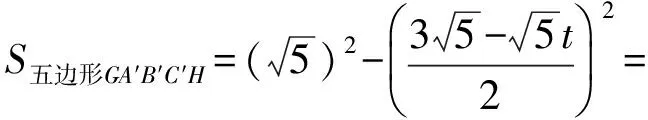简析以二次函数为背景的动态几何问题
2010-11-23张家港外国语学校江苏张家港215600
●(张家港外国语学校 江苏张家港 215600)
动态几何问题以其丰富的特性频频亮相于中考试题,尤其是与二次函数的结合,更加增添了动态几何的“个性”魅力.现采撷2009年中考试题几例作一简析,供学习参考.
1 单动点与二次函数
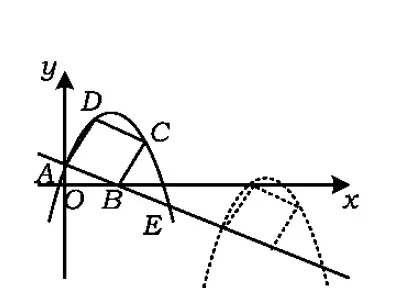
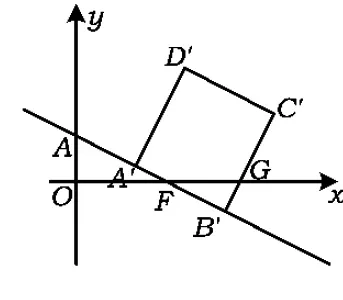
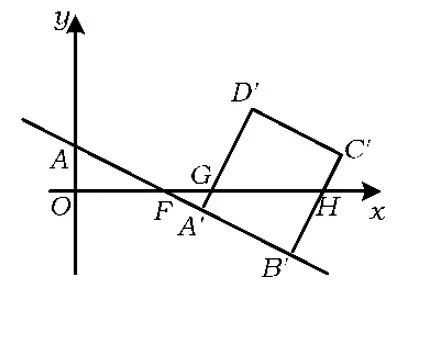
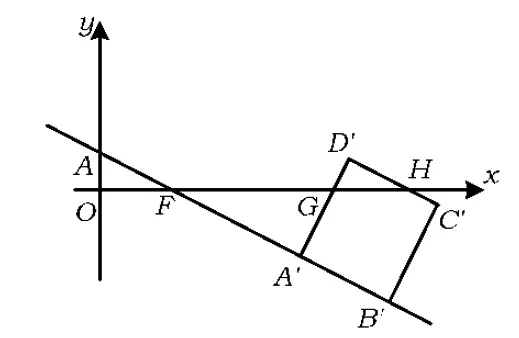
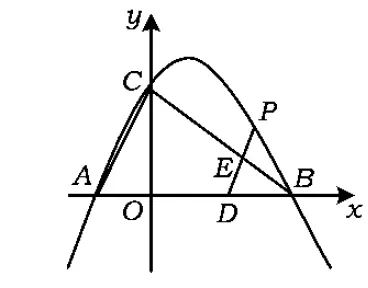
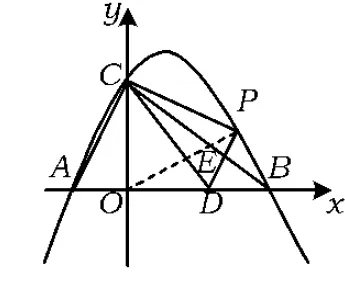
例1已知Rt△ABC的斜边长为5,斜边上的高为2,将这个直角三角形放置在平面直角坐标系中,使其斜边AB与x轴重合(其中OA 图1 图2 (1)求线段OA,OB的长和经过点A,B,C的抛物线的关系式. (2)如图2,点D的坐标为(2,0),点P(m,n)是该抛物线上的一个动点(其中m>0,n>0),连结DP交BC于点E. ①当△BDE是等腰三角形时,直接写出此时点E的坐标. ②连结CD,CP(如图3),△CDP是否有最大面积?若有,求出△CDP的最大面积和此时点P的坐标;若没有,请说明理由. (2009年深圳市数学中考试题) 解(1)设OA的长为x,则OB=5-x.由题意得OC=2,AB=5,∠AOC=∠BOC=90°,∠OAC=∠OCB,因此 △AOC∽△COB, 于是 CO2=OA·OB, 即 22=x(5-x), 解得 x1=1,x2=4. 又由OA OA=1,OB=4, 从而点A,B,C的坐标分别为A(-1,0),B(4,0),C(0,2).可设此二次函数的表达式为 y=a(x+1)(x-4), 将点C的坐标代入,得a=-0.5.故这个二次函数的表达式为 y=-0.5x2+1.5x+2. 图3 图4 ②如图4,连结OP,则 S△CDP=S四边形CODP-S△COD= S△COP+S△ODP-S△COD= 评析通过三点确定了抛物线的解析式;在分析△BDE是等腰三角形时,要抓住等腰三角形的特征,分3种情况进行讨论,即BD=BE,DB=DE,EB=ED;结合等腰三角形的三线合一来解题.由于是求△CDP的最大面积,因此要与二次函数的最值问题联系在一起,故要以△CDP的面积为因变量来建立二次函数. 例2如图5所示,在平面直角坐标系中,已知矩形ABCD的3个顶点B(4,0),C(8,0),D(8,8).抛物线y=ax2+bx过点A,C. 图5 (1)直接写出点A的坐标,并求出抛物线的解析式. (2)动点P从点A出发,沿线段AB向终点B运动,同时点Q从点C出发,沿线段CD向终点D运动.速度均为每秒1个单位长度,运动时间为t秒.过点P作PE⊥AB交AC于点E. ①过点E作EF⊥AD于点F,交抛物线于点G.当t为何值时,线段EG最长? ②连结EQ.在点P,Q运动的过程中,判断有几个时刻使得△CEQ是等腰三角形?请直接写出相应的t值. (2009年河南省数学中考试题) 解(1)点A的坐标为(4,8),将A(4,8),C(8,0)分别代入y=ax2+bx,得 解得 于是抛物线的解析式为 (2)①在Rt△APE和Rt△ABC中, 即 因此 从而 PB=8-t, 于是 评析由矩形的性质可知点A的坐标,近一步求得二次函数的解析式,为以下各小题打下伏笔;随着点P和点Q的运动,EF与抛物线的交点G始终在点E的上方,故EG的长等于点G的纵坐标与点E的纵坐标之差且它们的横坐标相同,所以可以通过建立二次函数来求最值.针对等腰三角形,根据点P,Q的运动分3种情况讨论即可. 例3如图6所示,在梯形ABCD中,AD∥BC,AD=6 cm,CD=4 cm,BC=BD=10 cm,点P由点B出发沿BD方向匀速运动,速度为1 cm/s;同时线段EF由DC出发沿DA方向匀速运动,速度为1 cm/s,交BD于点Q,连结PE.设运动时间为t(s)(0 (1)当t为何值时,PE∥AB. (2)设△PEQ的面积为y(cm2),求y与t之间的函数关系式. (4)连结PF,在上述运动过程中,五边形PFCDE的面积是否发生变化?请说明理由. (2009年山东省青岛市数学中考试题) 图6 图7 解(1)由PE∥AB,可得 而DE=t,DP=10-t,因此 解得 (2)由EFCD,可得四边形CDEF是平行四边形,因此 ∠DEQ=∠C,∠DQE=∠BDC. 又由BC=BD=10,得 ∠DEQ=∠C=∠DQE=∠BDC, 因此 △DEQ∽△BCD, 从而 解得 如图7,过点B作BM⊥CD,交CD于点M,过点P作PN⊥EF,交EF于点N,则 因为ED=DQ=BP=t,所以 PQ=10-2t. 又△PNQ∽△BMD,所以 即 解得 从而 (3) 解得 t1=1,t2=4. (4)在△PDE和△FBP中,由DE=BP=t,PD=BF=10-t,∠PDE=∠FBP,可得 △PDE≌△FBP, 因此S五边形PFCDE=S△PDE+S四边形PFCD= S△FBP+S四边形PFCD=S△BCD= 故在运动过程中,五边形PFCDE的面积不变. 评析由于线段的运动,因此四边形EFCD为平行四边形;利用相似或比例线段可用t的代数式表示三角形的底与高,故可求得函数解析式.针对五边形面积的定值问题,可利用等积变换转换成已求三角形的面积. (1)请直接写出点C,D的坐标. (2)求抛物线的解析式. (4)在第(3)小题的条件下,抛物线与正方形一起平移,直至顶点D落在x轴上时停止,求抛物线上C,E两点间的抛物线弧所扫过的面积. (2009年浙江省台州市数学中考试题) 图8 图9 解(1)C(3,2),D(1,3). (2)设抛物线方程为y=ax2+bx+c.由抛物线过点(0,1),(3,2),(1,3),可得 解得 于是 (3)①当点A运动到点F时,t=1.当0 所以 即 从而 ②当点C运动到x轴上时,t=2.当1 因此 图10 图11 因为 所以 即 于是 (4)如图12,因为 图12 所以 S阴影=S矩形BB′C′C= S矩形AA′D′D= AD×AA′= 评析随着正方形的整体移动,在x轴下方的部分分别为直角三角形、直角梯形和五边形,因此这个函数关系式应分情况进行讨论.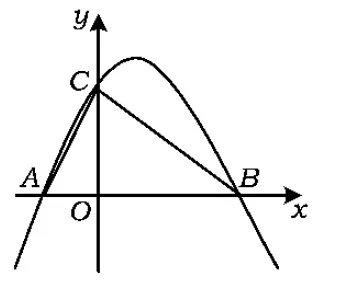


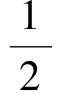

2 双动点与二次函数




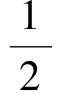
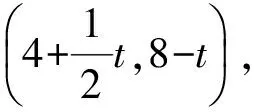
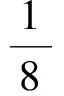
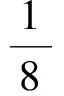

3 动线段与二次函数



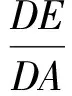
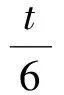




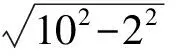
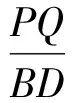
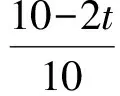



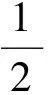
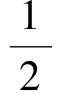


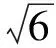
4 运动的封闭图形与二次函数