《数学通报》1786号问题的简证

●(鹿城区临江中学 浙江温州 325022)

《数学通报》2009年第5期刊登了曾昌涛教师提供的1786号问题的解答，过程较为繁琐，方法不易想到.现笔者提供如下一种简单的证法，供同行参考.

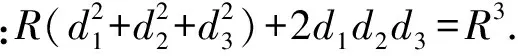
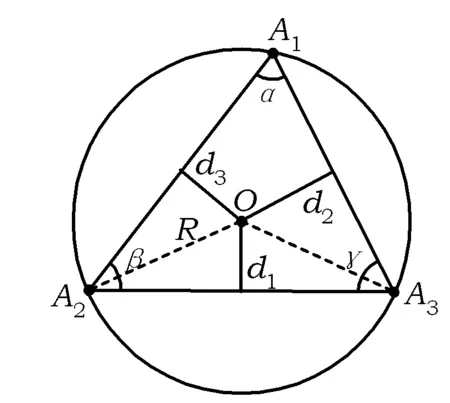
图1

简证如图1所示，连结OA2,OA3.设△A1A2A3的3个内角分别为α,β,γ.由圆心O在锐角△A1A2A3的内部，得

∠A2OA3=2α，A2A3=2Rsinα.

因为

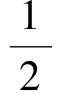
所以

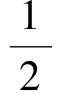
即

d1=Rcosα.

同理可得

d2=Rcosβ，d3=Rcosγ.

在三角形中，由三角恒等式可得,当α+β+γ=π时，

cos2α+cos2β+cos2γ+2cosαcosβcosγ=1，

因此

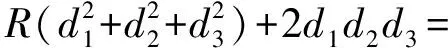
R3(cos2α+cos2β+cos2γ)+2R3cosαcosβcosγ=

R3(cos2α+cos2β+cos2γ+2cosαcosβcosγ)=

R3·1=R3,

故命题得证.

注原题中若去掉“锐角△A1A2A3”的限制，则结论可改为：

证明方法类似.