“平均变化率”教学设计

●(艾青中学 浙江金华 321000)

1 内容和内容解析

内容：平均变化率的概念及其求法.

内容解析：本节课是高中数学(选修2-2)第一章《导数及其应用》的第一节变化率与导数中的变化率问题.本节内容通过分析研究气球膨胀率问题、高台跳水问题，总结归纳出一般函数的平均变化率概念，在此基础上，要求学生掌握函数平均变化率解法的一般步骤.

本节课是起始课，对导数概念的形成起着奠基作用.平均变化率是个核心概念，它在整个高中数学中占有及其重要的地位，是研究瞬时变化率及其导数概念的基础.在这个过程中，要注意特殊到一般、数形结合等数学思想方法的渗透.

新课标对“导数及其应用”内容的处理有较大的变化，它不介绍极限的形式化定义及相关知识，也有别于以往教材将导数仅仅作为一种特殊的极限、一种“规则”来学习的处理方式，而是按照“平均变化率—瞬时变化率—导数的概念—导数的几何意义”这样的顺序来安排，用“逼近”的方法定义导数.这种概念建立的方式形象、直观、生动,又易于理解，突出了导数概念的本质.

教学重点：函数平均变化率的概念.

2 目标和目标解析

目标：理解平均变化率的概念，掌握求平均变化率的一般步骤.

目标解析：(1)经历从生活中的变化率问题抽象概括出函数平均变化率概念的过程，体会从特殊到一般的数学思想，体现了数学知识来源于生活，又服务于生活;

(2)在信息技术环境下，可以使实例的背景更形象、更逼真，从而激发学生的学习兴趣，通过演示平均变化率的几何意义让学生更好地体会数形结合思想;

(3)通过应用举例的教学，不断地提供给学生比较、分析、归纳、综合的机会，体现了从特殊到一般的思维过程，既关注了学生的认知基础，又促使学生在原有认知基础上获取知识，提高思维能力，保持高水平的思维活动，符合学生的认知规律.

3 教学问题诊断分析

(1)学生学情分析

现有知识储备:①直线的斜率；②物体运动的速度.

现有能力特征:具有一定归纳、概括、类比、抽象思维能力.

现有情感态度:对导数这一新鲜的概念具有强烈的求知欲和渴望探究的积极情感态度.

(2)对于平均变化率概念的理解，学生的认知困难主要在于：用准确的数学符号语言刻画图像变化的快慢速度，这种由形到数的翻译、从直观到抽象的转变对学生来说是比较困难的，因此在教学中可以从学生熟悉的身高变化、气温变化、气球膨胀、运动速度等这些背景简单的实际问题出发，利用图像的陡升引导学生发现函数值变化快慢的不同，并将这种不同用数学语言表达出来，从而使学生逐步概括出函数平均变化率的定义.

教学难点：函数平均变化率的概念.

4 教学支持条件分析

为了有效实现教学目标，准备计算机、投影仪、多媒体课件等增加课堂知识的交互性；用学生感兴趣的名人身高，儿时的吹气球游戏等寓教于乐，提高学生的兴趣和课堂效率；用奥运健儿成功的事例，让情感引领学生的学习热情.

5 教学过程

5.1 简单介绍、总体把握

(1)介绍微积分的创始人——牛顿和莱布尼茨.

设计意图：通过播放牛顿和莱布尼茨的图片(幻灯片展示)，向学生介绍微积分的产生是数学发展史上一个具有划时代意义的伟大创造，被誉为数学史上的里程碑.而牛顿和莱布尼茨在不断地探索与研究中，各自独立地创立了微积分，并对微积分的发展做了突出的贡献.使学生初步了解相关的数学文化，感知科学家们不懈求真的科学态度与精神.

(2)微积分与4类科学问题.

一是已知物体运动的路程作为时间的函数，求物体在任意时刻的速度与加速度;反之，已知物体的加速度作为时间的函数，求速度与路程.

二是求曲线的切线.

三是求函数的最大值与最小值.

四是求长度、面积、体积和重心等.

设计意图：利用章引言中提示的微积分的相关数学史，引导学生探寻微积分发展的线索，体会微积分的创立与人类科技发展之间的紧密联系，认识导数和定积分在研究和处理实际问题中的作用，从而激发学生学习本章内容的兴趣.笔者建议学完本章内容后，再次引导学生阅读章引言，以加深学生对导数的思想、方法和作用的体会.

5.2 创设情境，生成概念

5.2.1 实例分析、初探概念

情境1某运动员的身高曲线图

设计意图：把生活中某运动员的身高曲线图引入课题(如图1)，以激发学生的学习兴趣，为生成函数平均变化率提供实际背景.

师生活动：引导学生从图1中观察得到某运动员的身高随年龄的变化情况.在13～16年龄段中，身高增长最快.进一步探究得，需用“身高的增长量与年龄的增加量”的比值来刻画这一问题，而这个比值就是身高的年平均增长率,即平均变化率.

图1

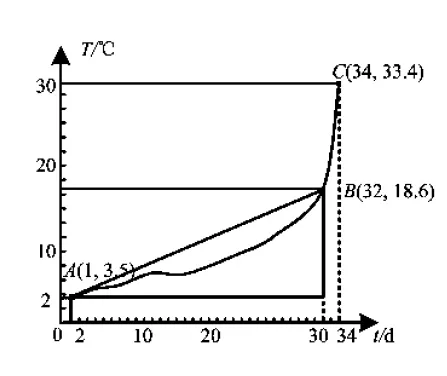
图2

情境2气温“陡升”

现有某市2009年3月18日至4月20日中某天的日最高气温记载,如图2所示.

设计意图：再次让学生从“形”中感受生活中的变化率问题——气温陡升，为生成函数平均变化率提供了又一个实际背景.

师生活动：引导学生从图2中观察得到温度的变化情况，进一步探究得到，需用“气温的增加量与时间的增加量”的比值来刻画气温变化的快慢，而这个比值就是气温的平均变化率.

5.2.2 探究过程、感悟概念

情境3气球平均膨胀率

在吹气球的过程中可以发现，随着气球内空气容量的增加，气球的半径增加得越来越慢.如何从数学的角度描述这种现象呢？

设计意图：“对生活现象作数学解释”不仅可以激发学生深入探究的兴趣，而且可以让学生感受到数学是有用的.问题中涉及到气球内空气容量，即气球体积V，气球半径r这2个变量.“随着气球内空气容量的增加，气球的半径增加得越来越慢”，从数学角度进行描述就是“随着气球体积的增大，半径的增加量与体积的增加量的比值越来越小”，而这个比值就是气球的平均变化率.

师生活动：一个学生利用打气筒给气球打气，连续打2次，每次打10下(尽量做到每次打入的空气体积相同)，让另一个学生用直尺测量2次的气球直径，直观感受气球的平均变化率.由球的体积公式推导出半径关于体积的函数解析式，然后通过计算，用数据来回答问题，解释上述现象.

思考：当空气容量从V1增加到V2时,气球的平均膨胀率是多少?

设计意图：把情境3中的具体数据运算抽象到一般的字母表示,为生成函数平均变化率概念作铺垫.

师生活动：教师播放多媒体，学生可以直接回答问题，教师板书其正确答案.

情境4高台跳水

在高台跳水运动中，运动员相对于水面的高度h(单位:m)与起跳后的时间t(单位：s)存在函数关系：h(t)=-4.9t2+6.5t+10.如果用运动员在某段时间内的平均速度描述其运动状态，那么：(1)在0≤t≤0.5这段时间里,运动员的平均速度是多少？(2)在1≤t≤1.5这段时间里，运动员的平均速度为多少？

设计意图：高台跳水展示了生活中最常见的一种运动，而运动速度是学生非常熟悉的物理知识，这样设计可以减少因为背景的复杂而可能引起的对数学知识学习的干扰.通过计算为生成函数平均变化率概念提供了又一实际背景.

师生活动：教师播放郭晶晶、吴敏霞在2008年北京奥运会上的跳水比赛录像，让学生重温奥运会的辉煌成就，从而进一步激发爱国热情，并在情境中感受速度变化.学生通过计算回答问题，对第(2)小题的答案说明其物理意义.

5.2.3 归纳概括、恰当表征

归纳定义：根据之前的4个情景，归纳概括出平均变化率的概念：

函数f(x)从x1到x2的平均变化率的定义：

令Δx=x2-x1,Δy=f(x2)-f(x1),则

设计意图：结合具体问题的实际意义,抽象得到变化率的定义,由浅入深、由易到难、由特殊到一般，完成了思维的飞跃.

探究1平均变化率的几何意义是什么？

设计意图：概念是文字表述，只是数量角度的描述，通过之前的例子，从图形角度体会平均变化率的几何意义.数形结合扫清了学生的思维障碍，更好地突破了教学的重、难点，体验数学的简约美.

师生活动：教师再次展示“气温陡升”的图片，引导学生仔细观察图像，直观感知、体会平均变化率的几何意义.

5.3 应用举例，强化概念

5.3.1 联系实际、感受平均变化率

设计意图：感受数学来源于生活，又服务于生活.

师生活动：鼓励学生思考并举例说明生活中平均变化率的例子,教师结合学生所举的实例进行恰当地分析和引导，揭示本质.

5.3.2 变式训练、巩固概型

探究2分别求以下函数在区间[1，2]上的平均变化率.

(1)f(x)=2;

(2)f(x)=-2x+1;

(3)f(x)=x2.

变式1求函数f(x)=x2在区间[-1,1]上的平均变化率．

变式2求函数f(x)=x2在区间[1,1.1],[1,1.01],[1,1.001]上的平均变化率.

设计意图：结合前面所学的3类基本初等函数感受平均变化率,加深学生对平均变化率内涵及几何意义的理解.变式1中平均变化率为“0”这一现象引起学生的好奇，进一步为联系“高台跳水”中平均速度为0，意识到平均速度只能粗略地描述物体在某段时间内的运动状态.为了能更精确地刻画出物体运动，有必要研究某个时刻的速度即瞬时速度，为下一节瞬时变化率的讲解作铺垫.

师生活动：每生一题，认真板演.教师巡视并规范过程.

5.4 归纳总结、内化知识

设计意图：让学生自己小结，不只是总结知识更重要的是总结数学思想方法.这是一个知识重组的过程，是一个多维整合的过程，也是一个高层次的自我认识过程，可以帮助学生自行构建知识体系，理清知识脉络，养成良好的学习习惯.

师生活动：学生小结，必要时其他学生补充、完善，教师适时点评.

6 作业布置、升华提炼

设计意图：作业是学生信息的反馈，在作业中可以发现和弥补教学中的不足，同时注重个体差异、因材施教.作业1是知识的巩固与升华；作业2起到承上启下的作用，并锻炼学生自主探究的能力.

(1)作业本：变化率问题第1页第2题.

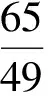
①运动员在这段时间里是静止的吗?

②你认为用平均速度描述运动员的运动状态有什么问题吗？

本教学设计的总体思路：荷兰数学家、数学教育家弗赖登塔尔从数学教育的特点出发，提出了以下4个数学教学的原则：“数学现实”原则，“数学化”原则，“再创造”原则，“严谨性”原则.笔者认为，对于本节课学习的概念“平均变化率”，学生的“数学现实”是他们非常熟悉的4个情境——身高变化、气温变化、气球膨胀、运动速度以及对相关图形的直观认识；在教师的引导下，通过学生自己的运算和思考，即“再创造”的过程，将形的问题用数量予以精确刻画；对4个问题的共同属性抽象概括而得出“平均变化率”的定义，即“数学化”的过程，再对定义进行变式，并从数和形2个角度加深对“平均变化率”的理解，最后实现对“平均变化率”概念的意义建构.