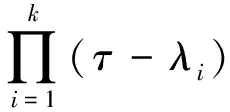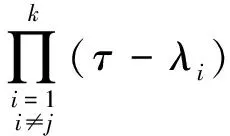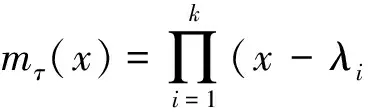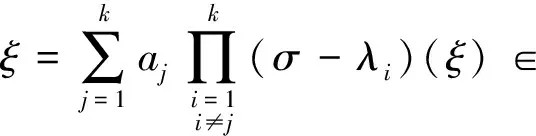The Note on Diagonalizable Linear Operators

HUANG Yun-bao

(College of Science, Hangzhou Normal University, Hangzhou 310036, China)

Theorem1([1], Theorem 8.11) A linear operatorτ∈() on a finite-dimensional vector spaceis diagonalizable if and only if its minimal polynomialmτ(x) is the product of distinct linear factors.

In what follows, we provide a new proof of Theorem 1 by making use of elementary symmetric polynomials of the eigenvalues of the operatorτ.

For a positive integern, leti∈{1,2,…,n},k∈{1,2,…,n-1} and letσk(i)(x1,x2,…,xn) (orσk(i)) denote thekth elementary symmetric polynomial inn-1 variablesx1,x2,…,xi-1,xi+1,…,xn, that is,

(1)

In general,we have

From (1) it immediately follows that

(2)

where form

Now we need to establish the following surprising result on the determinant composed of elementary symmetric polynomials.

Lemma1Let

(3)

then

(4)

ProofIn the determinant of (3), we add -1 times column 1 to column 2, column 3, …, and columnnrespectively, from (2) it follows

which implies (4).

ProofofTheorem1Letλ1,λ2,…,λkbe all different eigenvalues of the operatorτ. Ifτis diagonalizable, then from

(5)

which means

(6)

And it is easy to see

which leads to

(7)

Combining (6) with (7) gives

(8)

Conversely, ifmτ(x) is the product of distinct linear factors, then without loss of generality, we assumemτ(x) is of the form (8). It is sufficient to check (5) holds.

To do so, first, frommτ(τ)=0 it follows that

which means

(9)

as a linear combination of the vectorsξ,σ(ξ),…,σk-1(ξ) in order to obtain the following identical relation:

⋮

⋮

(10)

whereσm(i)=σm(i)(λ1,λ2,…,λk).

Now we consider the following system of equations inkvariablesa1,a2,…,ak:

(11)

Note that the coefficient determinant of the system of equations (11) is exactly equal to Δ(λ1,λ2,…,λk). Sinceλ1,λ2,…,λkare different from each other, from Lemma 2 we obtain Δ(λ1,λ2,…,λk)≠0.

according to (10) and (9). Thus (5) holds.

[1] Steven Roman. Advanced linear algebra[M]. 3th ed, Germany: Springer,2008:196-198.

[2] Zhang Herui, Hao Bingxin. Advanced algebra[M]. 5th ed, Peking: Advanced Education Press,2007:255-287.