对一个数学问题的探究

●(漳州市第一中学 福建漳州 363000)

在《数学教学》2008年第12期的数学问题与解答栏目中有这样一个问题：

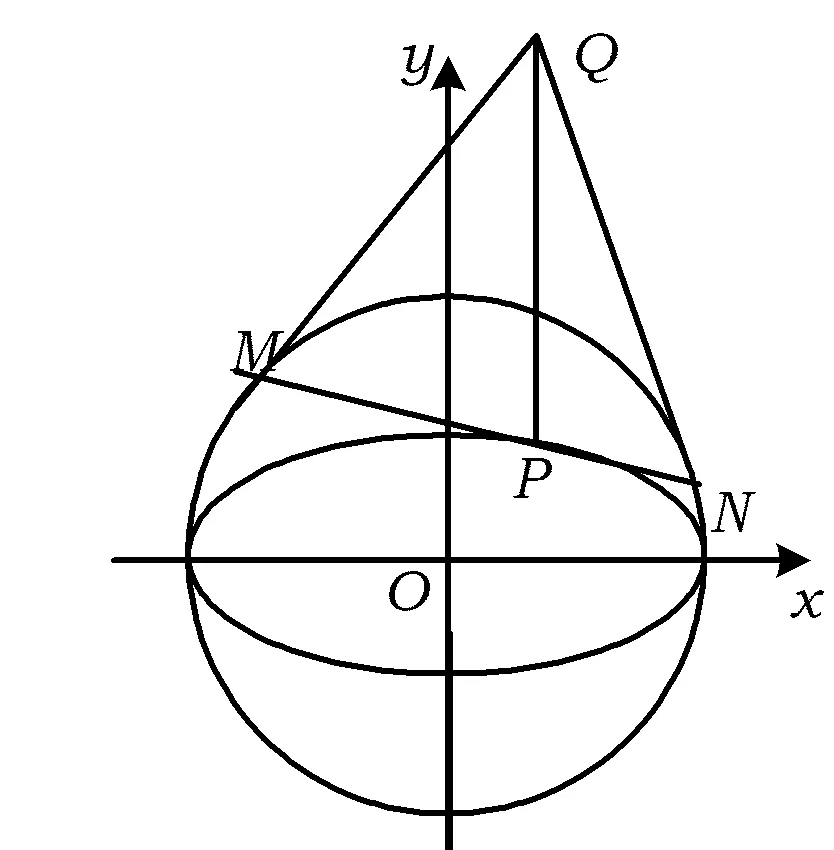
图1

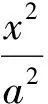
1 解法探究

《数学教学》2009年第2期上刊出了上述问题的解法，但较为繁琐.笔者对其证法作了探究，给出如下简单证法：

证明设Q(x0,y0)，M(x1,y1),N(x2,y2),则切线MQ,NQ的方程分别为

x1x+y1y=a2,x2x+y2y=a2.

由点Q在切线MQ,NQ上得

x1x0+y1y0=a2;x2x0+y2y0=a2，

因此直线MN的方程为

x0x+y0y=a2,

即

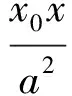
(1)

设P(x′,y′)，则椭圆在点P处的切线MN的方程为

比较式(1)，式(2),得x0=x′，所以PQ⊥x轴.

2 结论拓广

经过上述探究,可得到如下性质.

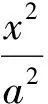
若将结论作引申拓广，则可得：

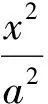
证明设Q(x0,y0),M(x1,y1),N(x2,y2)，则切线MQ,NQ的方程分别为

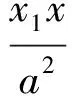
由点Q在切线MQ,NQ上得

因此直线MN的方程为

设P(x′,y′)，则圆O在点P处的切线MN的方程为

x′x+y′y=b2,

即

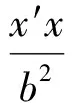
(4)

比较式(3),式(4),得y0=y′，所以PQ⊥y轴.

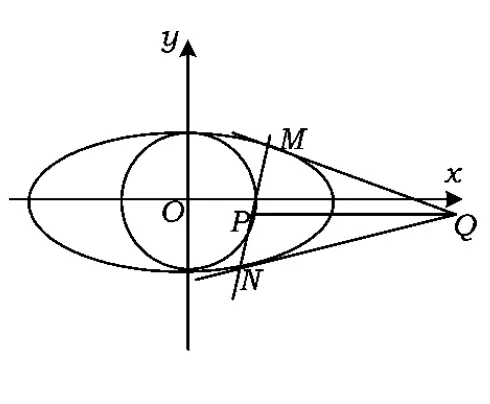
图2

图3

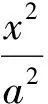
证明设Q(x0,y0),M(x1,y1),N(x2,y2)，则切线MQ,NQ的方程分别为

x1x+y1y=a2;x2x+y2y=a2.

由点Q在切线MQ,NQ上得

x1x0+y1y0=a2;x2x0+y2y0=a2.

因此直线MN的方程为x0x+y0y=a2,即

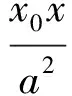
(5)

设P(x′,y′)，则双曲线在点P处的切线MN的方程为

比较式(5),式(6),得x0=x′，所以PQ⊥x轴.

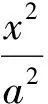
证明设Q(x0,y0),M(x1,y1),N(x2,y2)，则切线MQ,NQ的方程分别为

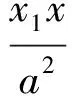
由点Q在切线MQ,NQ上得

因此直线MN的方程为

设P(x′,y′)，则圆O在点P处的切线MN的方程为

乐视的多元化经营管理的初期目标是正确的，可以整合企业的资源配置达到良好的资源优化分配效果但是在多元化经营当中企业应当依托核心优势以核心竞争力为内原动力,逐步扩张,尽量做到多元化扩张的产业与核心产业相关性较高。那么进一步思考乐视为什么跳出专业化向多元化进军呢？本文从企业的多元化经营战略的选择原则来分析。

x′x+y′y=a2,

即

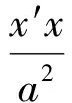
(8)

比较式(7)，式(8),得x0=x′，所以PQ⊥x轴.

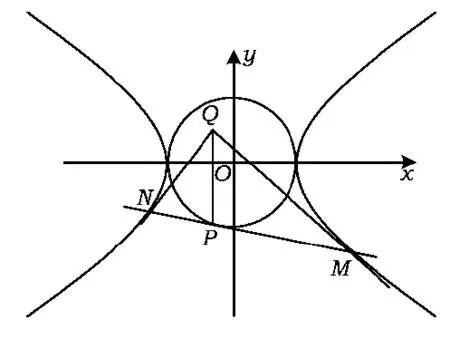
图4

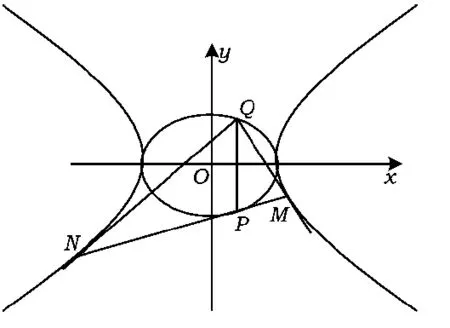
图5

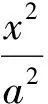
证明设Q(x0,y0)，M(x1,y1),N(x2,y2),则切线MQ,NQ的方程分别为

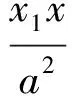
由点Q在切线MQ,NQ上得

因此直线MN的方程为

比较式(9),式(10),得x0=x′，所以PQ⊥x轴.

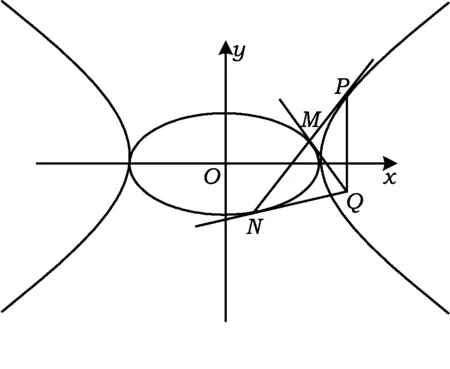
图6

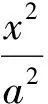
证明设Q(x0,y0)，M(x1,y1),N(x2,y2),则切线MQ,NQ的方程分别为

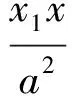
由点Q在切线MQ,NQ上得

因此直线MN的方程为

设P(x′,y′)，则双曲线在点P处的切线MN的方程为

比较式(11),式(12),得x0=x′，所以PQ⊥x轴.