发挥向量的工具功能 优化解题观念

●(义乌市第四中学 浙江义乌 322000)

向量是高中阶段的新增内容之一，它以其强大的工具性，在解决某些问题中越来越受到师生的重视，特别是近几年的高考对向量的考查更突出了向量作为工具的主体功能.它在很多情况下是和解析几何进行联系的桥梁，许多问题能用“老办法”解决，但利用向量解决会更合理，体现了高中课程改革内容的优越性和必要性.笔者通过以下几种情况，以解析几何题为例，详细分析向量的工具功能，充分体现出运用向量解题所发挥的效果.

1 题中直接给出向量信息

在一类解析几何题中明显给出了向量信息，学生能自然地联想到用向量的方法进行解题.

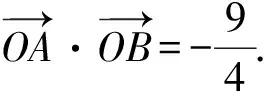
(1)求证：直线l经过一定点.

(2)设抛物线的焦点为F，∠AFB=θ,试问θ的值能否等于120°.若能，求出直线l的方程；若不能，请说明理由.

解(1)(用向量作为工具进行解题)设直线l：y=kx+b，把它代入抛物线方程x2=3y，整理得

x2-3kx-3b=0.

设A(x1,y1)，B(x2,y2)，由韦达定理知

x1+x2=3k,x1x2=-3b.

因为

所以

-4(x1x2+y1y2)=9.

又因为

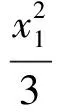
所以

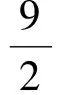
(2)方法1利用余弦定理，具体略.

方法2利用角公式，具体略.

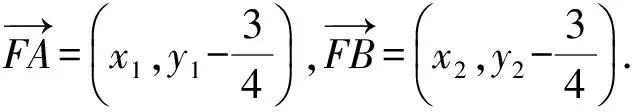
利用抛物线的焦半径公式,可知

因此

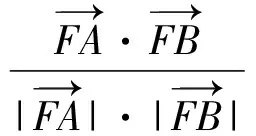
经整理得

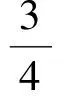
这与y1>0,y2>0矛盾,故∠AFB≠120°.

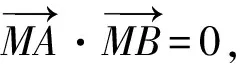
(1)求点C的轨迹D的方程；

(2)若直线l：y=k(x-1)与曲线D有2个不同的交点E,F，设P(-1，0)，当∠EPF为锐角时，求k的取值范围.

解(1)设M(1，m)，B(a，0)，则

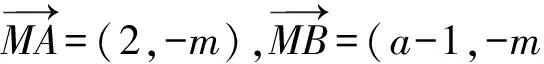
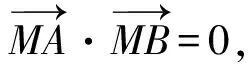
设C(x，y)，则

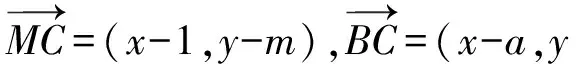
把式(2)代入式(1)并整理得

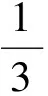
3k2x2+(1-6k2)x+3k2-1=0.

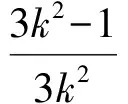
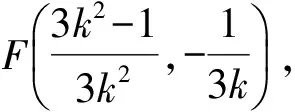
因为∠EPF为锐角，所以

解得

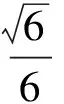
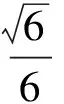
2 题中未直接给出向量信息

在实际解题过程中，许多解析几何题不会直接给出向量信息，而是隐藏在题目的某些信息中，这就要求学生有扎实的向量基础知识和敏锐的洞察力，发掘题干中的向量信息，运用向量知识简化解题过程.

图1

例3如图1,已知O为坐标原点，A，B为抛物线x2=2y上的点，且△OAB的面积S=t·tanθ，其中θ=∠AOB.

(1)求当t取最小值时，θ的最大值；

(2)求证：当t取最小值时，△OAB的垂心H在一条定曲线上，并求出此定曲线的方程.

解(1)设A(x1，y1)，B(x2，y2)，则

于是

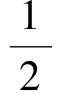
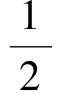
从而

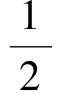
设直线AB：y=kx+b，代入抛物线x2=2y中,得

x2-2kx-2b=0，

于是

x1+x2=2k,x1x2=-2b，

因此y1y2=b2，则

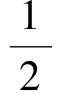
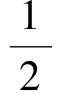
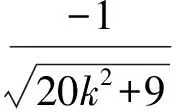
因为θ∈(0,π)，所以

(2)由第(1)小题知，直线AB的方程为y=kx+1.设H(x，y),则

因为H是垂心,所以

又由韦达定理知

x1+x2=2k,x1x2=-2.

上式经整理可得:y=-1.当k=0时,易求垂心H的坐标为(-1,0),适合上式,所以垂心H在一条定曲线上,定曲线的方程为y=-1.

回顾本题利用向量进行解题,避免了大量繁琐的运算过程,提高了解决这类问题的解题速度和准确率.