不同振子耦合系统固有频率的研究

朱仁义

（巢湖学院物理与电子科学系，安徽 巢湖 238000）

不同振子耦合系统固有频率的研究

朱仁义

（巢湖学院物理与电子科学系，安徽 巢湖 238000）

根据质心运动与相对运动建立耦合弹簧振子的动力学方程，通过特征根方程求解，确定系统固有频率，并加以讨论。

耦合弹簧振子；固有频率；振幅比

耦合弹簧振子系统的研究，无论在铁路运输、高速列车，还是在汽车运输过程中带有拖车，以及晶体学中格点的振动都广泛应用，且涉及到弹簧振子的耦合问题。例如，一列火车是多节车厢挂接在一起，每节车厢可以看作一个弹簧振子，从一维振动角度来分析火车，可以简化多弹簧振子串联。在工程上常常用多弹簧振子的串联来描述一个实际力学系统，因此，分析由多个振子串联而成的系统的运动规律，是一件有意义的工作。过去研究多半是假设耦合振子质量相同，弹簧的劲度系数相同。[1]本文将讨论一般情况下振子的耦合，首先，建立耦合弹簧振子质心运动和相对运动下动力学方程，其次，解其特征根方程，再讨论各种弹簧振子的耦合情况乃至极端情况。

1 系统的动力学方程

如图1所示，取m1物体的平衡位置为坐标原点，水平向右为x轴正方向，弹簧的自然长度为L0，任意时刻两物体的位置坐标分别为x1、x2。

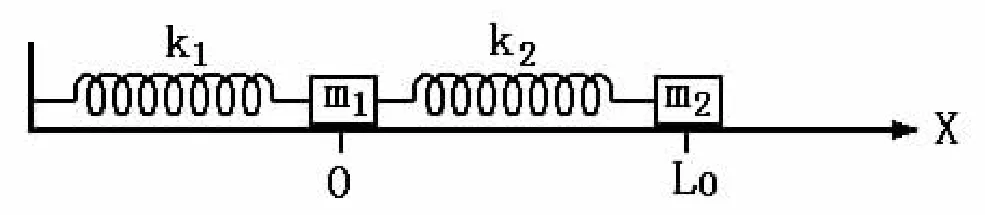
图1

根据牛顿第二定律，有：

作简单的变换，令 x′2=x2-L0、再用 x2代替 x′2得：

为了了解系统的运动规律，往往要知道整体的运动，即质心的运动，以及各部分之间的运动即相对运动。为此，引入取质心坐标xc和相对坐标xr[2]（不是严格的系统质心坐标与相对坐标）

2 系统动力学的本征解

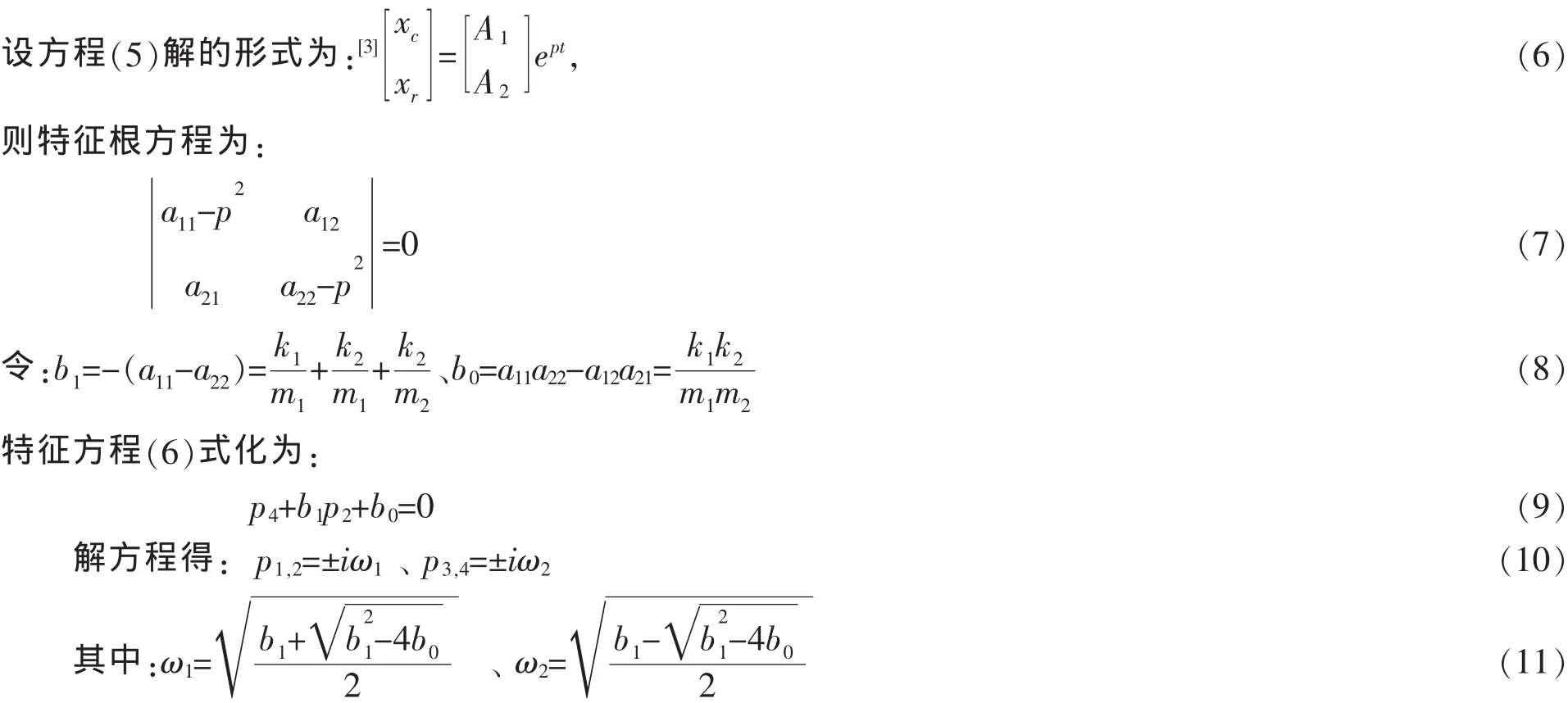
因为，b21-4b0＞0，所以以上四个解都是纯虚数，p1，2和p3，4为两对共轭复数。每对共轭复根，对应一个振动模式，说明系统质心围绕着平衡作周期性振动，它的振动是圆频率为ω1、ω2简谐振动的叠加。同理，两振子相对运动也为周期性振动，它的振动是圆频率为ω1、ω2简谐振动的叠加，这种运动称为固有振动或主振动。ω1、ω2称为系统固有频率。

3 各种耦合的振动频率ωi的讨论

下面就可能出现的各种耦合振动进行讨论。

物理意义非常清楚，从振子1角度来看，由于振子m1的质量非常大，振子2就可以看成振子1附属物，且可以忽略，系统的质心基本取决于m1的位置。也就是说，系统整体运动简化为m1在弹簧1作用下运动，其振动频率是大家熟知ω2；从振子2角度来看，由于振子m1的质量非常大，其振动极其缓慢，可以视为静止，振子2的振动就回归为我们熟知单振子的振动。

物理意义也很明确，弹簧1的劲度系数很大，相当于一根刚性杆将1物体连接固定起来，振动频率极高。振子2连接在刚性物体上，因而振子2的振动就回归为我们熟知单振子的振动，其振动频率就是自身的固有频率。

（5）两振子质量相近，但弹簧劲度k2≫k1

对于弹簧1来说，m1与m2用劲度系数很大的k2连接，就相当于用刚性杆连接，如图2所示，其振动圆满频率由（15）式中ω2决定。对于讨论m1与m2振子相对运动来说，由于它们之间用倔强系数很大的k2连接，相互作用力很大，弹簧1对系统的作用力可以忽略不计，模型可以简化为如图（3）来表示。振动圆频与（15）中 ω1一致。

图2

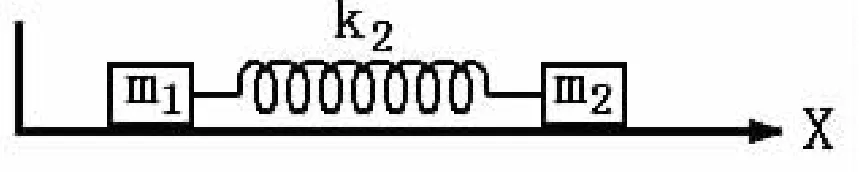
图3

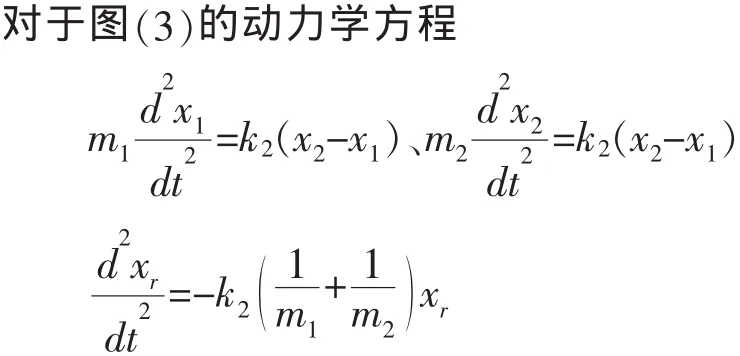
4 系统的运动情况

将（11）式代入（6），再代入（5）式可得到相应的振幅比值：

ri称为振幅比，由（16）式看出，振幅比由系统本身物理特性决定，而与初始条件无关，也是系统的固有属性。

将本征解（10）式代入（6），同时考虑到（16）可得：

其中 C1、C2、ω1、φ2，由系统的初始条件确定。 从（17）不难看出，系统在振动过程中，各质点同时到达平衡位置或最大位移，而在整个振动过程中，各质点位移比值将始终保持不变。

5 结束语

两个线性弹簧振子的耦合，其固有频率有两个，只决定于系统本身的物理特性，振子作周期性振动，其运动是两简谐振动的叠加得到。考虑到外加激励时，为了防止共振，激励的频率应避开两固有频率。

[1]杨正波，夏清华.耦合弹簧振子系统的研究[J].高等函授学报（自然科学版），2008，2（1）.

[2]周衍柏，理论力学教程[M].北京：高等教育出版社，1984.

[3]胡少华，苗同臣.结构振动理论及其应用[M].北京：中国建筑工业出版社，2005.

STUDY ON THE NATURAL FREQUENCY OF COUPLING SYSTEM FOR DIFFERENT OSCILLATORS

ZHU Ren-yi
（Department of Physics and Electronic Science，Chaohu University，Chaohu Anhui 238000）

According to the motion of mass center and relative motion，the dynamic equation of coupling spring oscillator was established in this thesis.Based on the solution of latent root equation，the natural frequency of the system was determined and discussed.

coupling spring oscillator； natural frequency； amplitude ratio

O32

A

1672－2868（2010）06－0053－04

2010－09－16

朱仁义（1958－），男，安徽和县人。高级实验师，研究方向：理论物理。

责任编辑：宏 彬