圆形隧道断面检测数据拟合新方法＊

谷 川 秦世伟

(1)上海市政工程设计研究总院,上海 200092 2)上海大学土木工程系,上海 200072)

圆形隧道断面检测数据拟合新方法＊

谷 川1)秦世伟2)

(1)上海市政工程设计研究总院,上海 200092 2)上海大学土木工程系,上海 200072)

针对圆形隧道断面检测数据拟合算法存在的不足,提出一种新的数据拟合算法。该算法首先对所有的观测点进行平面拟合,而后将所有的观测点进行球壳拟合,该球壳的球心必须位于拟合的平面内,并且在拟合的流程中加入粗差检验。该方法避免了坐标投影、坐标转换、迭代计算等复杂操作,可以直接得到空间圆的圆心、半径等参数。该模型可靠,拟合精度高,实现简便,节省计算资源,是一种良好的圆形隧道断面拟合算法。

断面检测;圆形隧道;平面拟合;球壳拟合;粗差检验

1 引言

随着现代城市的发展,轨道交通建设正在发生日新月异的变化,地铁由于其相对独特的优点,正越来越被人们认可。所以,地铁隧道的安全性要求也越来越高,如何保证地铁列车在隧道中安全运行成为了轨道交通管理部门所面临的首要任务。由于长时间的运行,同时大多数地铁隧道上方都是高层建筑,地铁隧道难免会发生一些变形,必须时刻掌握这些变形,并保证其处于安全范围之内,才能保证地铁列车的安全通行。

目前已有的方法多是首先对观测数据进行平面拟合,将观测点投影到拟合平面上,采用坐标转换的方式将三维坐标转换到平面内,基于点到圆心的距离与半径之差的平方和最小的原则,在平面内进行平面圆的拟合得到圆心和半径,将平面圆的圆心经过坐标反算转换到原坐标系中,得到空间圆的圆心[1-3]。应用该方法进行空间圆的拟合是可行和有效的,然而,其算法中涉及到坐标投影、两次坐标转换,平面圆拟合时对非线性的处理需要迭代等,原理比较复杂,实现起来比较繁琐。

文献[4]提出了一种采用空间平面和球壳相交的方法拟合空间圆,但由于没有对球壳进行限制,测点沿平面法线方向的误差对球壳方程的拟合扰动很大,抗差性不强;而且在拟合得出球壳的球心和半径等参数后,还需要进一步的计算才能得到空间圆的圆心、半径等参数,方法不够直接有效;此外,对于所有的观测点均位于同一空间圆上的特殊情况,理论上会得到无数组的解。

基于以上几点考虑,作者对现有方法进行了改进,提出了圆形隧道断面检测数据拟合新方法。该方法首先拟合得出观测点所在的空间平面,而后在球心坐标位于拟合平面内的约束下拟合空间球壳,得到的球心坐标和球壳半径即为空间圆的圆心坐标和半径。

2 隧道断面检测外业测量

对隧道断面的检测首先要保证测量断面位置正确,这样才可以和该断面的设计断面类型进行比对,其次要保证所测量的断面位于该里程点的法线方向,并且同时还要考虑纵断面方向的影响,所测的断面可能并不位于垂直面内,需要根据该里程点的坡度进行调整。

具体操作方式为：在需要进行断面测量的里程上某点设站,按照该里程的切线方向进行定向,将仪器旋转 90°到断面法线方向,然后以免棱镜模式进行断面点测量。如果采用的仪器为自动全站仪,则还可以根据需要设置按照固定的角度步长或者距离步长进行断面扫描测量。

隧道断面检测现场数据采集情况如图 1所示。

数据采集完成后,需要完成的工作就是对采集的数据进行处理,得到断面特征数据,例如圆心坐标、断面半径等。

3 空间圆拟合新方法的模型

3.1 空间平面拟合

理论上而言,断面测量的点应该位于空间的同一个平面内,为了实现最终的断面曲线拟合,首先必须找到该空间平面。但是,由于数据采集误差 (主要指观测点位置偏离检测断面)的存在,断面点可能不完全在同一个空间平面内,则需要按照最小二乘原理剔除粗差。

图1 隧道断面检测现场数据采集Fig.1 Data acquisition in tunnel section detection site

以 (Xi,Yi,Zi)T(i=1,2,…,n)表示观测点坐标,则隧道断面的平面方程可表示为:

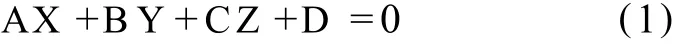
式中(A,B,C)T为平面的法线方向单位矢量,为了唯一确定该单位矢量,可令A＞0;若 A=0,则令B＞0;若A=0且B=0,则 C＞0;A、B、C不可能同时为0。

各观测点到平面的距离为：

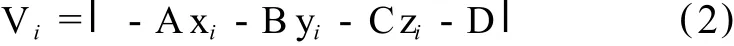
为了拟合出与观测值最接近的平面,可令各观测点至平面的距离平方和为最小,按最小二乘法则VTV=min,拟合出平面方程参数 A、B、C、D。条件式为A2+B2+C2=1,对A、B、C作单位化修正。

拟合时可以根据残差剔除数据采集粗差点。若某观测量改正残差大于限差 (如限差为 3σ,或某个设定值,或者同时满足两个条件),则视该观测量为粗差点。剔除粗差后根据最小二乘法则重新解算待估参数,找到最佳平面。本文采用同时满足Vi＞3σ和Vi＞±1 mm两个条件。

3.2 空间圆拟合新方法

空间平面与球壳的关系可以有如下的描述：

由于空间圆可由一个空间球壳与一个空间平面相交来描述。因此,可将观测数据分别拟合成一个平面和一个空间球壳,用平面和空间球壳相交表示该空间圆。即：

平面唯一,但是,球壳却可以有无穷多个,只要球壳的半径 R满足:

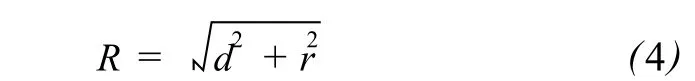
式中,d为球心到平面的距离,r为空间圆的半径。

为了使球壳唯一,可对其进行限制。本文提出将其限制为该球壳的球心位于该拟合平面上。如此,则观测点沿平面法线方向的扰动在空间圆径向方向的方向余弦为 0,即平面拟合的误差对球壳拟合没有影响。

该方法的原理如图 2所示。

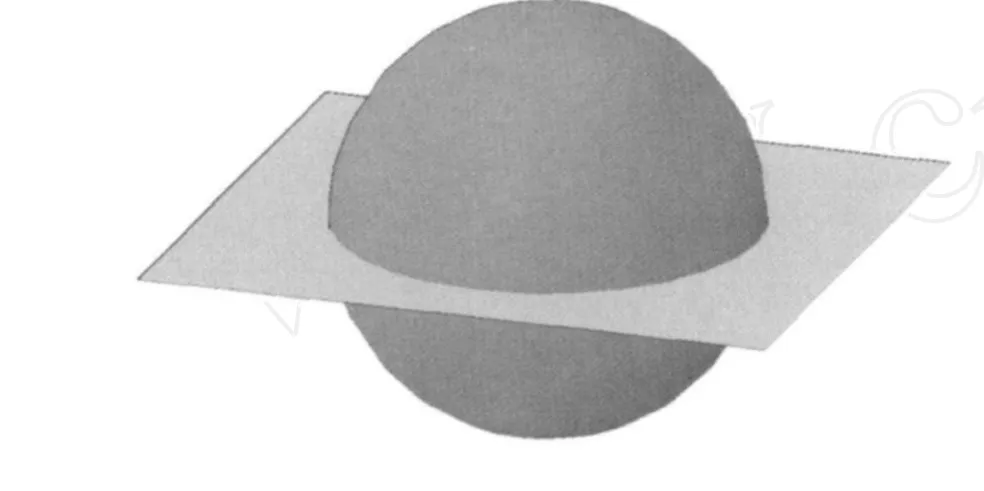
图2 空间圆拟合原理示意图Fig.2 Sketch of principle of space circle fitting

空间圆的表达方式为：

3.3 空间球壳拟合方法

球壳一般方程式为：

展开得：

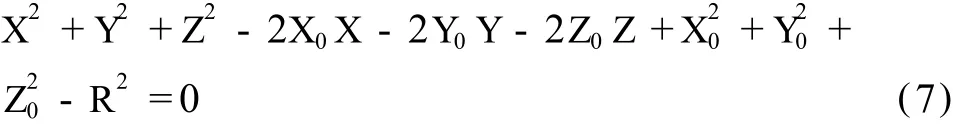
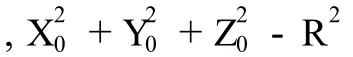
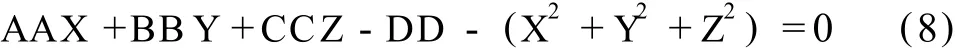
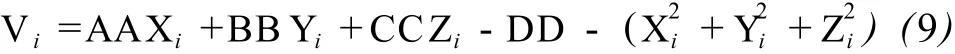
误差方程线性化为:

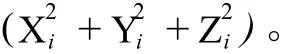
也可以写成:

式中,Ai=[XiYiZi-1],X=[dAA dBB dCC dDD]T。

对 X0、Y0、Z0加以约束,球心位于拟合平面上,

即满足公式：

亦即：

结果表明，当瓷介质磨矿时，随着pH值升高，方铅矿矿浆电位逐渐下降。但在铁介质磨矿下，随着pH值升高，方铅矿矿浆电位先略微下降，而后逐渐上升，且两种介质矿浆电位的差值随pH的升高而减小。因为当瓷介质磨矿时，方铅矿表面一直存在局部电池作用，消耗了溶解氧含量，磨矿系统氧化性越来越弱，导致矿浆电位下降。而当铁介质磨矿时，不仅矿物自身氧化溶解，存在局部电池作用，铁球介质还会发生氧化反应生成Fe2+和Fe3+，在低pH值情况下矿浆电位降低是两者的综合作用结果。但是随着pH值的升高，铁介质氧化加剧，不断生成高价铁离子，矿浆电位又会迅速上升。

按照附有限制条件的间接平差解算式 (11)、(14),就可以得到 X。

反算公式为：

求得的球心坐标即为空间圆的圆心坐标,球壳半径即为空间圆的半径。

拟合时可以根据残差剔除测量粗差点,若某观测量改正残差大于限差 (如限差为 3σ,或某个设定值,或者同时满足两个条件),则视该观测量为粗差点。剔除粗差后根据最小二乘法则重新解算待估参数。

采用本文的方法进行圆形隧道断面检测数据拟合的数据处理流程见图 3。

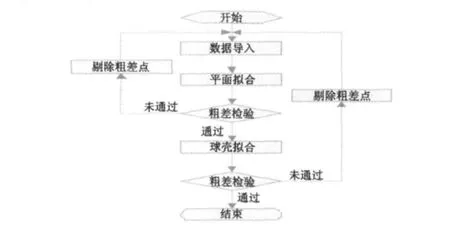
图3 数据处理流程Fig.3 Flow of data processing

3.4 初值的确定

好的初始值能够使计算更加精确,现给出初始值确定的方法。

4 算例

某隧道断面检测现场采集的数据如表 1。

采用 3种方法进行拟合,并且对拟合结果进行比较和分析。

方法Ⅰ为文献[1-3]中的方法,方法Ⅱ为文献[4]中的方法,方法Ⅲ为本文方法。

每种方法平面拟合的结果为：A=6.137 127× 10-9,B = -0.999 999 999 989 085,C = -4.672 165 308×10-6,D=-3.898 419 077 8× 10-5,平面拟合中误差为:σ=0.03 mm。

1)方法Ⅰ拟合结果

拟合得到圆心坐标为:X0=0.028 09,Y0= -0.000 01,Z0=-7.765 44,半径 R=2.764 49,拟合中误差σ=11.38 mm。

2)方法Ⅱ拟合结果

表 1 观测点坐标(单位:m)Tab.1 Coordinates of observed points(un it:m)

直接拟合得到球壳的方程参数为:X0= 0.028 09,Y0=2.184 92,Z0= -7.764 39,R= 2.185 09。空间圆圆心和半径参数为:X0= 0.028 09,Y0=0.000 00,Z0= -7.765 41,R= 2.764 50,拟合中误差σ=11.38 mm。

3)方法Ⅲ拟合结果

空间圆拟合结果为:X0=0.028 09,Y0= 0.000 00,Z0=-7.765 41,R=2.764 50,拟合中误差σ=11.38 mm。

采用上述几种方法进行数据处理,得到了几乎完全一致的计算结果,误差在 0.1 mm以下,可认为几种方法等效。按照本文的粗差剔除方法,T63为粗差点,被发现和剔除。在现场,T63为在管壁上的一个螺帽上采集的点。

观测点以及拟合圆弧位置的关系如图 4所示。

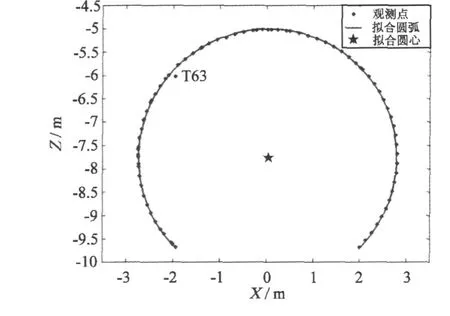
图4 观测点以及拟合圆弧Fig.4 Observed points and fitted circular arc

经过比较可以发现,3种方法仅存在0.01 mm数位的差别,考虑到测量误差远大于 0.01 mm,可以认为 3种方法得到的拟合结果几乎完全一致。但考虑到本文提出的方法无需坐标投影、坐标转换、迭代计算,且拟合解稳定,可直接得到拟合参数,便于程序实现,节省计算资源,所以本文的方法相对已有的数据处理方法更具优势。

5 结论

针对圆形隧道断面检测数据拟合方法存在的问题,提出了一种新的数据处理算法。该方法避免了坐标投影、坐标转换、计算迭代等操作,同时可以直接得到空间圆的圆心、半径等参数,方法实现简便,节省计算资源,拟合精度高,算法可靠,是一种良好的隧道断面拟合算法。

1 王解先,赵向阳.圆形轨道变形测量[J].工程勘察,2003, 31(4)：60-61,64.(Wang Jiexian and Zhao Xiangyang. Deformation surveying of circular orbit[J].Geotechnical Investigationamp;Surveying,2003,31(4),60-61,64)

2 潘国荣,谷川,施贵刚.空间圆形物体检测方法与数据处理[J].大地测量与地球动力学,2007,(3)：28-30. (Pan Guorong,Gu Chuan and Shi Guigang.Themethod and data processing for 3D circular object[J].Journal of Geodesy and Geodynamics,2007,(3)：28-30)

3 高俊强,陶建岳.利用免棱镜全站仪进行地铁遂道断面测量与计算[J].测绘通报,2005,51(10)：41-43.(Gao Junqiang and Tao Jianyue.Profile survey and computation of the subway tunnel using total-station instrument without prism[J].Bulletin of Surveying and Mapping,2005,51 (10)：41-43)

4 潘国荣,陈晓龙.空间圆形物体数据拟合新方法[J].大地测量与地球动力学,2008,(2)：92-94.(Pan Guorong and Chen Xiaolong.A new method for 3D circular object fitting[J].Journalof Geodesy and Geodynamics,2008,(2)：92-94)

A NEW M ETHOD FOR FITTING DETECTION DATA OF C IRCULAR TUNNEL SECTION

Gu Chuan1)and Qin Shiwei2)

(1)ShanghaiM unicipal Engineering Designamp;Research General Institute,Shanghai 200092 2)Depart m ent of Civil Engineering,Shanghai University,Shanghai 200072)

Aiming at deficiencies of existing fitting algorithms for detection data of circular tunnel section,a new data fittingmethod isproposed.Firstly,allobserved points are fitted to a plane.After that,allobserved points are fitted by using a sphere modelwhose centermust be in the fitted plane.Incorrect observed data will be excluded during the fitting process.The new method can avoid coordinates projection,coordinates transfor mation and iteration calculation,etc.The parameters such as center and radius of circle can be gotten directly.The calculation model is reliable and easy to realize,which is usefull to get high fitting precision.The new algorithm takes less calculation resource so it can be considered to be a good tunnel section fitting algorithms.

section detection;circular tunnel;plane fitting;sphere fitting;error detection

1671-5942(2010)05-0097-05

2010-04-23

谷川,男,1983年生,工学博士,工程师,主要研究方向为市政工程桥隧检测、监测.E-mail：guchuanhaha@163.com

P226+.1

A