抗差自适应无味粒子滤波＊

秦 臻 高井祥 王 坚

(中国矿业大学国土环境与灾害监测国家测绘局重点实验室,徐州 221116)

抗差自适应无味粒子滤波＊

秦 臻 高井祥 王 坚

(中国矿业大学国土环境与灾害监测国家测绘局重点实验室,徐州 221116)

针对系统观测值含有粗差或者存在状态异常的情况,基于无味粒子滤波算法 (UPF)和抗差自适应滤波原理,提出了一种新的抗差自适应无味粒子滤波算法(AR-UPF)。该方法采用方差膨胀模型抑制观测粗差的影响;利用自适应UKF算法来实时调整状态参数预报值的协方差,控制状态异常的影响。算例分析表明,新方法能够有效地控制观测粗差与状态异常,提高了滤波精度。

无味粒子滤波;抗差自适应滤波;抗差自适应无味粒子滤波;方差膨胀;滤波精度

1 引言

无味粒子滤波算法(UPF)是一种非线性滤波算法,它是在粒子滤波 (PF)的基础上[1],采用 Unscented Kalman滤波(UKF)生成 PF的建议分布,每一次采样后的粒子都使用UKF算法进行更新,所得均值和方差用于下次粒子采样,解决了传统 PF算法中以转换先验密度函数作为建议分布所引发的各种问题[2]。目前,UPF算法已逐渐应用于目标跟踪[3,4]、导航[5]等领域。在实际应用中,由于仪器操作不当或者其他原因会造成观测异常,而状态异常也会影响状态参数的估值。系统存在异常,会导致粒子权重选取错误,致使 UPF算法滤波精度降低。利用抗差自适应滤波原理[6],构造合理的等价权函数以及自适应因子,进而控制状态异常与观测异常对粒子权重的影响。本文在UPF算法的基础上,提出了AP-UPF算法,并设计了 3种计算方案,通过比较表明,新方法的滤波结果稳定,不仅能有效地抑制观测值粗差的影响,而且能够抵制状态异常对状态滤波估值的影响。

2 UPF算法

UPF算法步骤如下[7]：

3)根据该建议分布函数抽取新的粒子。

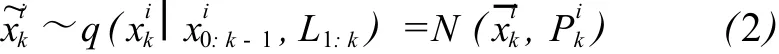
4)计算粒子的权值。

5)权重进行归一化。

7)UPF滤波结果为:

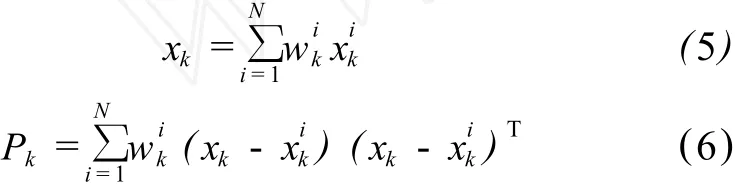
3 抗差自适应滤波

抗差自适应滤波的基本思想是,当观测值存在异常,则对观测值采用抗差估计原则[8];当动力学模型存在异常,则将动力学模型信息作为一个整体,采用自适应因子调整动力学模型信息对状态参数的整体贡献[9]。基于此,改进的UPF算法采用方差膨胀原理来调节观测噪声的协方差;通过构建自适应UKF重点采样模型实时调节状态噪声的协方差,从而控制观测异常与动态模型异常对状态参数的影响。

假设系统动力学方程与观测方程为[8,9]：

其中,wk是系统噪声矩阵,协方差矩阵为 Pwk,vk是观测噪声矩阵,协方差矩阵为 Pvk;wk与 vk不相关,且都为高斯白噪声。

3.1 观测噪声等价协方差的确定[10]

观测噪声等价协方差通过方差膨胀模型来获得。观测噪声的协方差阵反映观测值的离散程度,若观测值精度高,可靠性好,则相应观测值的方差就小,从而该观测值在状态估计中所占的权重就大;反之,若观测值含有粗差,可靠性差,则相应观测值的方差就大,从而该观测值在状态估计中的权重就小。所以,通过适当扩大异常观测的方差来降低异常观测对参数估值的影响。

假设观测值不相关,只考虑方差元素,则观测值yk的方差为如果 yk中含有粗差,令其中,βk为膨胀因子,为等价方差。

膨胀因子可以构造为:

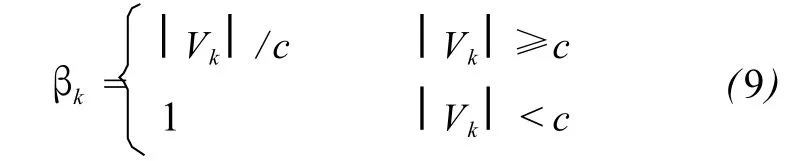
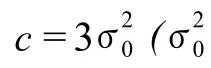
通过构造出的膨胀因子βk可以看出,当观测值含有粗差时,即观测误差超出一定限值时,其相应的方差膨胀;反之,方差保持不变。

3.2 自适应状态参数协方差的确定

如果系统状态发生异常时,需要通过调节状态噪声协方差来控制动态模型噪声异常对状态参数估值的影响。基于自适应滤波思想和UKF算法,利用自适应因子实时调整状态参数协方差,从而控制动态模型异常对参数的影响。具体计算步骤如下：

1)计算自适应因子αk

采用状态不符值统计量作为自适应因子的判别统计量[6,11]。设为状态预报值,为状态抗差解,为状态预报值与状态抗差解的差值,当相差较大时,则认为系统状态发生异常。

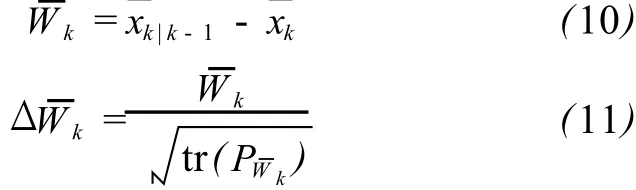
其中,tr(·)为求迹运算。自适应因子分段函数形式为[12]:

其中,c为常数,取值范围为 1.0～2.5。

2)计算 Sigma点集

Sigma点相应的权值:

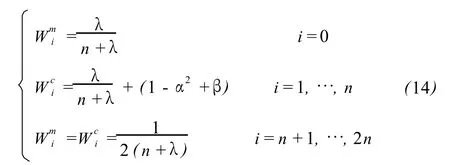
其中:n为状态向量维数;λ为合成比例参数,λ的值为α2(n+κ)-n;α为正的缩放比例参数,它控制粒子分布的距离,所以应取较小的数值,一般选α=1; κ通常为 0;β用于融入随即变量的验前信息。

将式(14)得到的采样点代入状态方程,得到预测采样点点集:

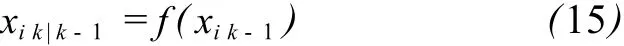
同理,将式(16)得到的预测采样点代入观测方程,得到预测测量点点集:

3)预测、更新阶段

根据所求得的 Sigma点集及其权值可得:

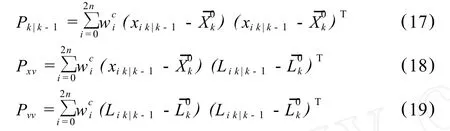
其中,Pk|k-1是预测采样点的方差,Pvv、Pxv分别为预测测量点的方差和协方差;和为状态方程和观测方程的 Sigma点集的均值。

4)自适应滤波协方差的确定

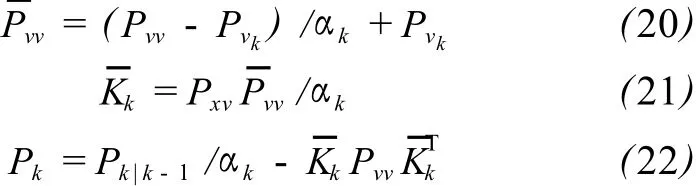
4 技术路线

AP-UPF算法的基本思想是通过方差膨胀原理求得观测噪声的等价协方差,利用自适应UKF算法得到重点密度函数,然后,利用其重点密度函数代替经典 PF粒子滤波的重要密度函数。技术流程见图1,具体步骤如下：

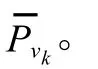
5)重采样。根据有效粒子数判断退化情况,重新生成一个新的粒子集合{i=1,…,M},且满足6)状态更新。

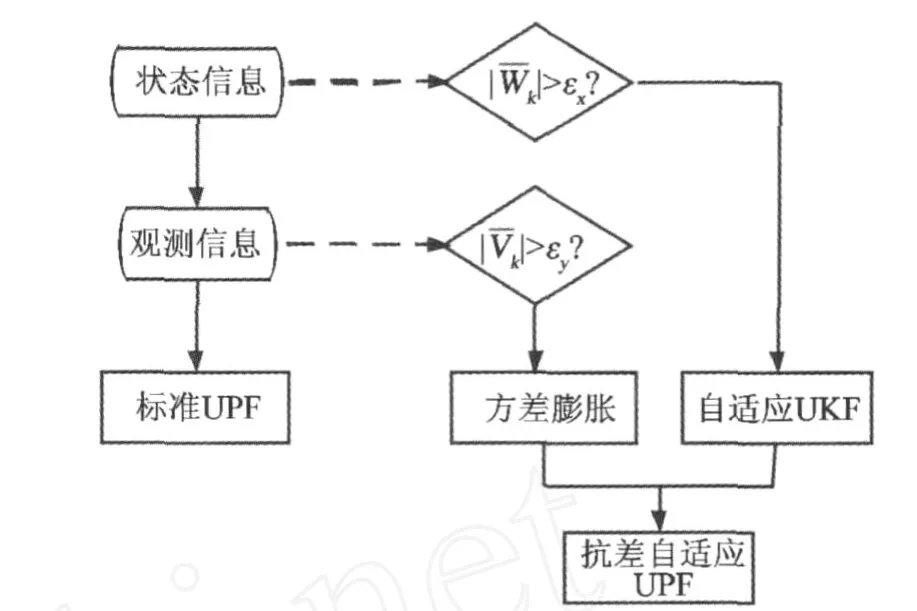
图1 AR-UPF技术流程Fig.1 Technical flow ofAR-UPF

5 算例分析

5.1 仿真验证

首先采用非线性较强的标量模型算例对算法进行仿真验证,状态方程及观测方程如下:

式中:wt和 vt均为独立的高斯白噪声序列,其中,wt～N(0,5),vt～N(0,0.1)。仿真粒子数为 200,仿真历元数为 200,采样间隔为 1 s。分别运用标准UPF算法和抗差自适应 UPF算法进行比较计算,3种方案如下：1)观测值与动态模型都无异常;2)50～100历元间加入连续观测粗差、动态模型无异常; 3)动态模型异常、观测值无异常。3种方案的计算结果与真值的差值曲线见图 2～6,对应的 RMS见表1。

由图 2可知,在模型没有异常的情况下,UPF算法与AP-UPF算法滤波结果基本一致,只是由于粒子选取的随机性,粒子权重的选取存在细微差别。当观测值加入连续性粗差,与图 2(a)相比,UPF算法滤波结果 (图 3(a))受粗差的影响较大,滤波精度明显降低;而 AP-UPF算法对异常观测值的方差进行膨胀处理,从而减小了粗差对粒子权重的影响,从误差曲线(图 3(b))可以看出,AP-UPF算法起到一定的抵制粗差的效果;图 2(b)与图 3(b)相比,后者的误差曲线也受到粗差的影响,这是由于模型的非线性程度较高,非线性模型误差较大引起的。当状态发生异常时,通过图 4可知,AP-UPF算法通过构造自适应因子调整动态模型协方差,从而降低了状态异常对 UKF重点密度采样过程的影响。综合以上分析,抗差自适应UPF从理论上不仅能够抵制观测异常的影响,而且对状态异常具有较强的控制能力。

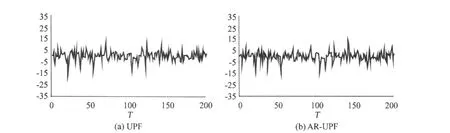
图2 无异常时UPF与AR-UPF的误差曲线Fig.2 UPF and AR-UPF error curveswithout anomalies

图3 观测异常时UPF与AR-UPF的误差曲线Fig.3 UPF and AR-UPF error curveswith measurement outliers

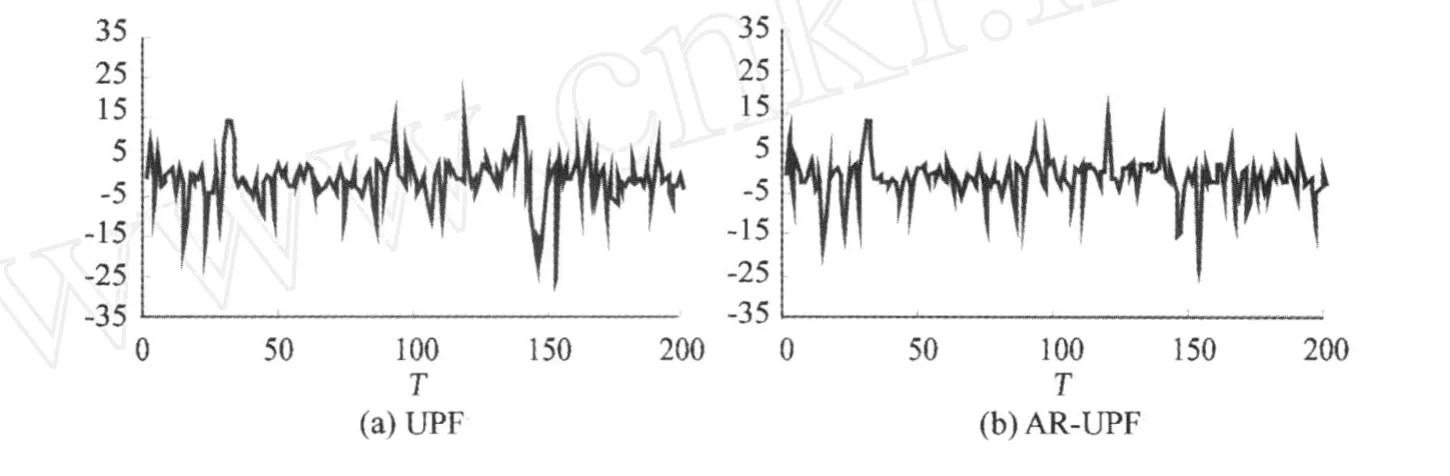
图4 状态异常时UPF与AR-UPF的误差曲线Fig.4 UPF and AR-UPF error curveswith state anomalies

表 1给出了 3种方案的RMS误差统计结果,可以看出第一种方案中AP-UPF算法的 RMS误差与UPF算法基本相等,而后两种方案中 AP-UPF算法的RMS误差均小于UPF算法,这与图 2～4的滤波结果分析相一致。

5.2 实例分析

为了实际分析抗差自适应无味粒子滤波算法的性能,真实算例选取 2009年 12月 6日采集的 GPS动态定位数据,实验利用自行研制的 GPS动态定位实验平台,实验地点选取为中国矿业大学主楼广场前,数据采集频率为 1 s。初始化时间为 30分钟,目的是保证初始定位坐标的精度;实验平台做大范围机动,其运动轨迹见图 5。解算中利用高精度的差分定位结果作为参考值,单点伪距定位进行各种滤波解算,其结果与参考值的差值进行比较。滤波过程中,初值 X0、P0由静态定位给定,状态模型动态噪声方差阵Q取为对角阵,对角元素均为 5×10-4,观测噪声方差阵 R也取对角阵,对角元素均为 5 m2。取 100历元,分别采用以下 3种方案进行处理：

方案 1：扩展卡尔曼滤波(EKF);

方案 2：UPF(粒子数 1 000);

方案 3：AP-UPF(粒子数 1 000)。

图 6～8中,坐标系横轴表示观测历元,纵轴表示滤波输出与参考值之差,图中只给出X分量的坐标差,Y、Z方向的坐标差与 X分量相似。滤波输出量统计结果见表2。

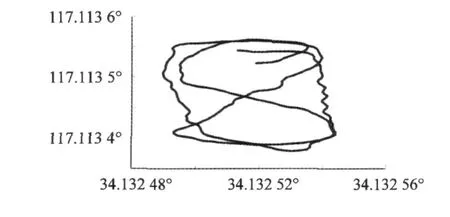
图5 载体运动轨迹平面图Fig.5 Vehicle tracking

图6 EKF残差Fig.6 Residual errors of EKF

图7 UPF残差Fig.7 Residual errors ofUPF

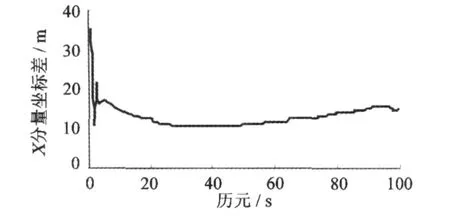
图8 AP-UPF残差Fig.8 Residual errors ofAP-UPF

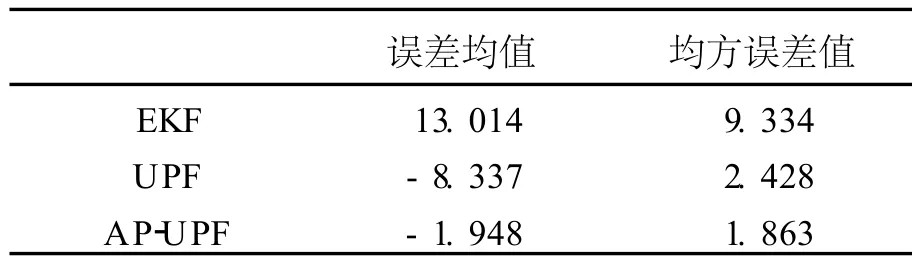
表 2 两种滤波输出的误差统计结果(单位:m)Tab.2 Error results of filtering output by different algorithm(un it:m)

结合滤波图,分析上述统计结果可知：1)从图 5可以看到,扩展 Kalman残差曲线经波动后再趋于平稳状态,这是由于滤波初值选取的可靠性直接影响扩展 Kalman滤波收敛的效率;2)分析图 6、7和表 2可知,与扩展 Kalman滤波相比,UPF算法对 GPS动态定位精度有明显的提高,经滤波后 GPS位置定位精度在 X分量上接近 8 m,在扩展 Kal man滤波基础上,精度提高了 36%。精度提高的原因主要是无味粒子滤波通过UT变换结合蒙特卡罗模拟方法来实现递推贝叶斯滤波,用于非线性状态模型和观测模型的动态滤波系统,从而避免了线性化而忽略高次项所带来的舍入误差;其次,无味粒子滤波不要求观测噪声和动力学模型噪声为高斯白噪声,能够较好地抵制有色噪声的影响;第三,无味粒子滤波充分考虑到了观测值的影响,克服了传统粒子算法中粒子发散问题;3)分析图 7、图 8和表 2可知,与UPF算法相比,AP-UPF算法定位精度为 2 m,精度提高了75%。精度提高的原因为 GPS做大幅度机动或GPS信号受到干扰时,观测值受到污染,此时新算法通过对异常观测值的方差进行膨胀处理,通过构造自适应因子调整动态模型协方差,从而降低了状态异常对UKF重点密度采样过程的影响,从而明显地提高了 GPS动态定位精度。

6 结语

针对观测值含有粗差或状态发生异常的情况,本文提出抗差自适应UPF算法。它是UPF滤波与抗差自适应滤波相结合的算法。其独特之处在于它能够自适应地控制动态模型异常与观测异常的影响,不仅合理地平衡了动力学模型预报信息与观测信息的权比,而且一定程度上抵制了粗差对粒子重要性权重的影响。通过仿真分析与实际算例结果,与UPF算法相比,抗差自适应UPF算法具有一定的抗差性,说明该算法是一种有效算法。对于如何降低非线性误差的影响与完善自适应因子的结构等方面,有待于进一步改进。

1 Chen Z.Bayesian filtering：from Kalman filters to particle filters,and beyond[R].Hamilton：McMaster University, 2003.

2 Mer we R V,et al.The unscented particle filter[R].Technical Report CUED/F-I NPENG/TR 380,Cambridge University EngineeringDepartment,2000.

3 Guo Ronghua and Qin Zheng.An unscented particle filter for ground maneuvering target tracking[J].Journal of Zhejiang University(Science A：An International Applied Physicsamp; Engineering Journal),2007(10)：1 588-1 595.

4 李景熹,王树宗.UPF算法及其在目标跟踪问题中的应用[J].系统仿真学报,2007,19(3)：675-677.(Li Jingxi andWang Shuzong.UPF algorithm and its application on target tracking problem[J].Journal of System Simulation, 2007,19(3)：675-677)

5 隋树林,等.UPF在探测器自主导航中的应用[J].微计算机信息,2008(4)：287-288.(Sui Shulin,et al.The use of unscented particle filter in the probes autonomous navigation [J].Microcomputer Information,2008,(4)：287-288)

6 杨元喜.自适应动态导航定位[M].北京：测绘出版社, 2006.(Yang Yuanxi.Adaptive navigation and kinematic positioning[M].Beijing：Publishing House of Surveying and Mapping,2006)

7 Julier S J andUhlmann J K.A new method for the nonlineartransformation of means and covariances in filters and estimators[J].IEEE Trans.A.C.(S0018-9286),2000,45 (3)：477-482.

8 杨元喜.自适应抗差最小二乘估计[J].测绘学报,1996, (3)：207-211.(Yang Yuanxi.Adaptively robust least squares estimation[J].Acta Geodaetica Et Cartographic Sinica,1996,(3)：207-211)

9 杨元喜,等.论动态自适应滤波[J].测绘学报,2001,30 (4)：293-298.(Yang Yuanxi,et al.Adaptive robust filtering for kinematic GPS Positioning[J].Acta Geodaetica Et Cartographic Sinica,2001,30(4)：293-298)

10 Yang Yuanxi,et al.Robust estimator for correlated observations based on bifactor equivalent weights[J].Journal of Geodesy,2002,76(6/7)：353-358.

11 Yang Yuanxi,et al.Adaptively Robust Filtering for Kinematic Geodetic Position[J].Journal of Geodesy,2001,75 (2)：109-116.

12 聂建亮.采用自适应Unscented Kal man的粒子滤波[J].大地测量与地球动力学,2008,(3)：87-91.(Nie Jianliang.Particle filter based on daptive unscented Kalman filter[J].Journal of geodesy and geodynamics,2008,(3)：87-91)

13 李涛.非线性滤波在导航系统中的应用研究[D].国防科技大学,2003.(Li Tao.Research on application of nonlinear filtering in navigation system[D].NationalUniversity ofDefense Technology,2003)

ROBUST ADAPTIVE SCENTLESS PARTICLE FILTER

Qin Zhen,Gao Jingxiang andWang Jian
(China University of M ining and Technology,Key Laboratory forLand Environm ent and D isasterM onitoring of SBSM,Xuzhou 221116)

In order to resist the bad influence ofmeasurement outliers and state model errors,a new robust adaptive unscented particle filter isproposed,which is based on unscented particle filter algorithm and adaptively robust filter theory.First,the new method uses the variance expandingmodel to resistmeasurementoutliers.Second, the adaptive unscented Kalman filter(UKF)is used to adjust the covariance of state predicted value,and to reduce the influence of state model errors.The examples have proved that the new procedure of the robust adaptive unscented particle filter is feasible and efficient.

unscented particle filter(UPF);robust adaptive filter;RobustAdaptive Unscented Particle Filter(ARUPF);variance inflation;precision of the filter

1671-5942(2010)05-0144-06

2010-05-23

国家自然科学基金(40904004);教育部博士点基金(200802900501amp;200802901516);江苏省自然科学基金(BK2009099)

秦臻,男,1986年生,硕士研究生,主要从事 GNSS测量数据处理研究.E-mail：qinzhen-614@163.com

P207

A