逆向工程椭圆柱构件的拟合计算＊

雷婉南 赵鹏飞

(1)同济大学测量与国土信息工程系,上海 200092 2)上海市测绘院,上海 200063)

逆向工程椭圆柱构件的拟合计算＊

雷婉南1)赵鹏飞1,2)

(1)同济大学测量与国土信息工程系,上海 200092 2)上海市测绘院,上海 200063)

提出一种基于逆向工程原理的拟合椭圆柱构件的方法：使用电子全站仪采集椭圆柱形工业构件表面的离散点坐标,通过拟合椭圆柱底面获取法向量,从而进行坐标转换,将空间任意位置的椭圆柱转换为标准形式,将椭圆柱的拟合问题转换为椭圆的拟合问题。并用工程实例证明了该方法的可行性。

椭圆柱构件;平面拟合;坐标转换;椭圆拟合;逆向工程

1 引言

现代工业构件的检测工作具有数据采集量大、点位测量要求精度高、数据要求可靠度高等特点,传统的丈量尺寸的检测方法已经逐渐不能适应其需要。所以目前工业构件的检测大多采用逆向工程的原理：通过使用测量仪器,采集待测工业构件特征位置的一系列点的坐标,通过对这些坐标进行拟合计算,对比设计数据,从而达到对工业构件进行检测的目的。

在工业领域中,椭圆柱状的工业构件有很多,包括油罐、气罐、运输罐、沥青罐等储罐类构件,以及其他椭圆柱型的工业构件等等。文献[1]提出一种将特征值也作为参数的二次曲线拟合方法;文献[2]提出利用神经网络进行椭圆柱面拟合的方法,但这两种方法的数学模型均较为复杂。本文通过研究椭圆柱的几何性质,提出一种拟合椭圆柱的简单方法：以最小二乘原理为基础,通过坐标转换将空间任意位置的椭圆柱转换为标准位置的椭圆柱,从而达到拟合计算的目的。

2 椭圆柱底面的拟合

平面方程通常表示为

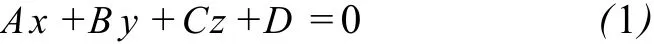
很显然,若方程两边可以同时乘上一个比例系数,所得方程依然表示该平面。所以,为方便起见,令系数D=1,则平面方程改写为

根据最小二乘法原理,每组观测点 (xi,yi,zi)的误差方程为:

令:

则误差方程改写为:

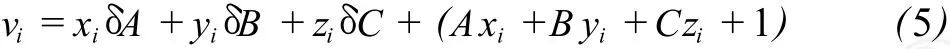
利用在椭圆柱底面上测量得到的 n个点的坐标,建立 n个误差方程,通过间接平差的方法便可求出平面方程的3个参数。

如果对椭圆柱的两个底面都进行了测量,那么可以列出两套误差方程:

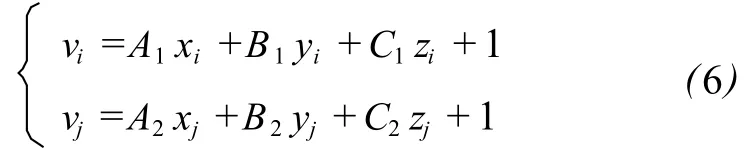
由于椭圆柱两个底面是平行的,所以上下两个平面方程的参数满足条件:

可以结合式(6)和式(7),按照附有条件的间接平差模型进行解算,即可求出这两个平面方程。

3 计算平面的法向量

式(1)、式(2)为平面方程的一般表达式,同样平面可以表达为如下的法式表达式:

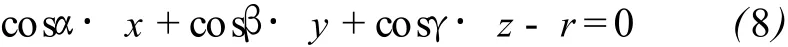
式中,α、β、γ为平面法向量分别与 X、Y、Z3个坐标轴的夹角,r为法向量的长度。式 (2)和式 (8)都为同一平面的表达式,所以对应系数满足:

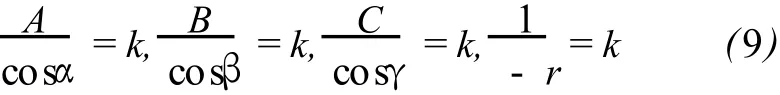
又根据向量夹角余弦定理,有:

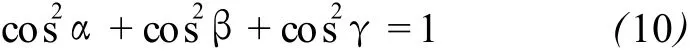
通过式(9)和(10),解得

考虑式(9)中 r与 k的关系,如果规定法向量长度为正,则 k取负值。所以平面法向量可表达如下:

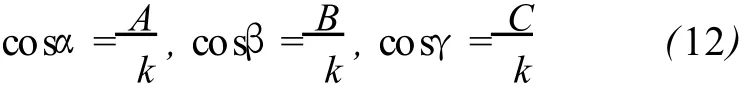
法向量的方位角α方位角和天顶距 Z天顶距分别为:

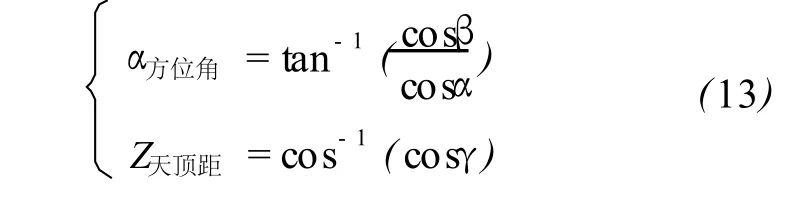
4 计算坐标转换参数

在工业检测中,所采集的数据是在工程坐标系(X,Y,Z)中所得到的坐标数据,该坐标系在空间的位置是任意的。为了方便对椭圆柱构件进行拟合计算,建立自定义坐标系 (X′,Y′,Z′),并规定:在自定义坐标系中,Z′轴与椭圆柱的中心轴平行。

图1 工程坐标系和自定义坐标系Fig.1 Engineering coordinate system and self-defined coordinate system

根据椭圆柱底面法向量的方位角和天顶距,对工程坐标系 (X,Y,Z)和自定义坐标系 (X′,Y′,Z′)进行转换。

1)工程坐标系 (X,Y,Z)转换为自定义坐标系(X′,Y′,Z′)

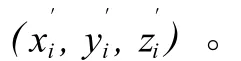
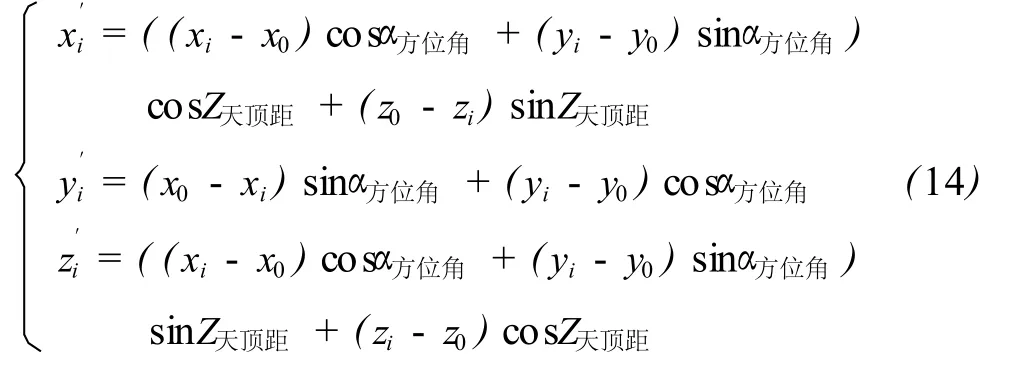
式中,(x0,y0,z0)为坐标转换的平移参数,也就是自定义坐标系的坐标原点在工程坐标系中的坐标,其值可取为椭圆柱底面测量坐标的平均值:

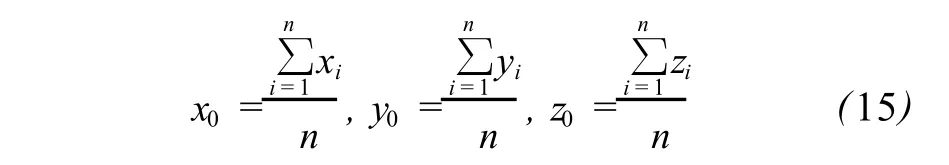
2)自定义坐标系 (X′,Y′,Z′)转换为工程坐标系(X,Y,Z)

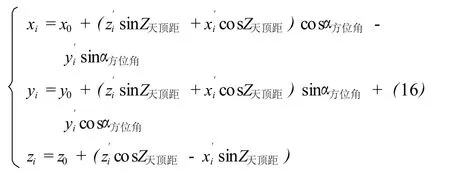
式中,(x0,y0,z0)同式 (14)。

5 椭圆的拟合

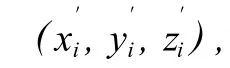
椭圆的拟合思路如下:椭圆属于二次曲线,所以先按照二次曲线进行拟合,然后对比相应参数,最终获得椭圆的拟合参数。

1)二次曲线拟合

二次曲线的方程为:

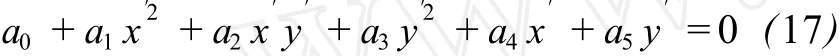
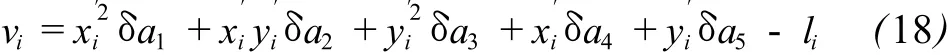
a0的值可以取为 x′坐标和 y′坐标的最大值与最小值之差的乘积,参数 a1、a2、a3、a4、a5的迭代初值可以取为 0。迭代求解至收敛,从而求得各系数。

2)椭圆参数的求解

平面椭圆的标准方程可表达为

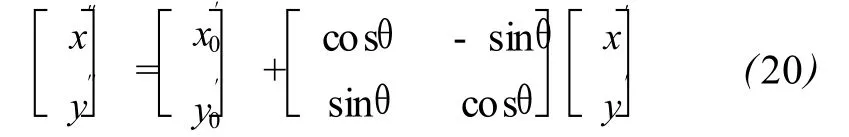
将式 (20)代入 (19),得:

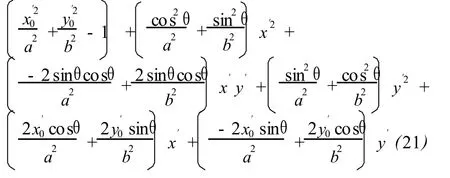
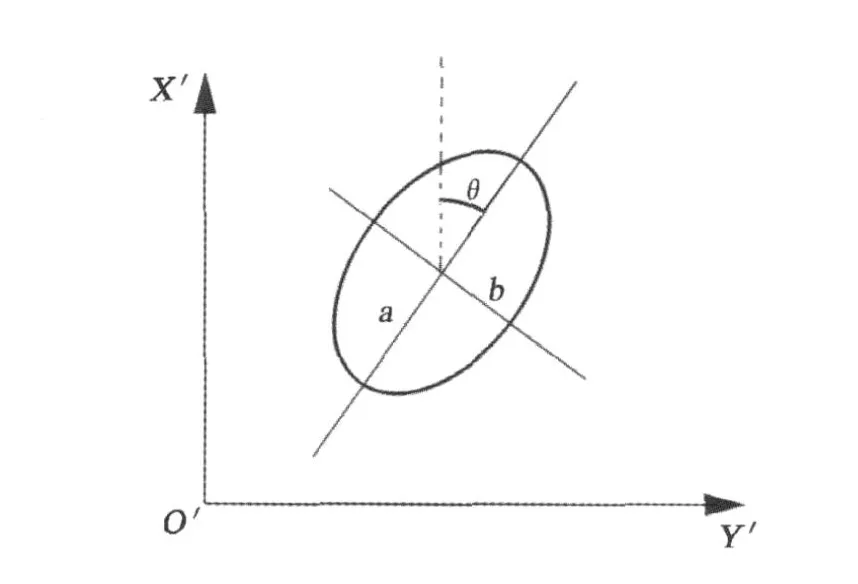
图2 椭圆的表示Fig.2 Scheme of an ellipsis

对照式(17)和 (21),最终求得椭圆的参数为:

6 工程实例

笔者受托对某厂生产的一批大型储油罐进行抽样检测。储油罐为卧式钢罐,截面为椭圆形,检测的目的是测定其实际截面尺寸是否符合设计尺寸,要求偏差控制在 3 cm之内。储油罐的设计尺寸为13.35 m×3.52 m×2.78 m,即截面椭圆的长轴为3.52 m,短轴为 2.78 m。

所以截面椭圆的设计标准方程为

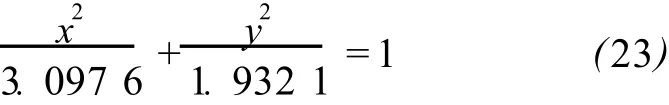
通过索佳NET1200全站仪 (其标称精度为：测角 0.5″,测距 1+1×10-6)对构件表面点的三维坐标进行采集,坐标测量采用全站仪无棱镜模式。共采集 48个点的三维坐标：其中 8个点在储油罐底面上,用以拟合底面方程;其余 40个点在储油罐侧壁上,分为 5组,每组 8个点,同一组的点形成的平面大致平行于底面 (图 3),相邻平面之间距离为 2 m左右。

1)底面方程拟合及其法向量的计算

表 1列出底面上所采集的 8个点的三维坐标。

图3 储油罐侧壁采样数据Fig.3 Sample data on the lateralwall of oil tank

表 1 储油罐底面的采样数据(单位:m)Tab.1 Sample data on the bottom face of oil tank(un it: m)

首先,将底面采集数据进行拟合,得到底面的平面方程。

然后,经过计算得到椭圆柱底面的法向量,进而计算出法向量的天顶距和方位角分别为 Z天顶距= 89.267 934°,α方位角=29.799 627°。

2)坐标转换和椭圆拟合

表 2列出了储油罐侧壁上测量得的 40个点的三维坐标。

按照本文方法将 40组坐标由工程坐标转换为自定义坐标。然后用转换后的坐标拟合椭圆 (图4)。

得到椭圆的标准方程为

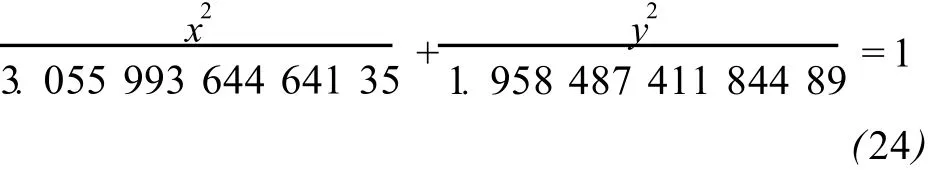
即长轴为 3.496 3 m,短轴为 2.798 9 m。可见,储油罐界面的长短轴与其设计尺寸的偏差控制得较好,均在 3 cm之内,所以认为储油罐的尺寸是合格的,也证明了本文模型是可行的。

7 结论

表 2 储油罐侧壁的采样数据(单位:m)Tab.2 Sample data on the lateral wall of oil tank(un it: m)

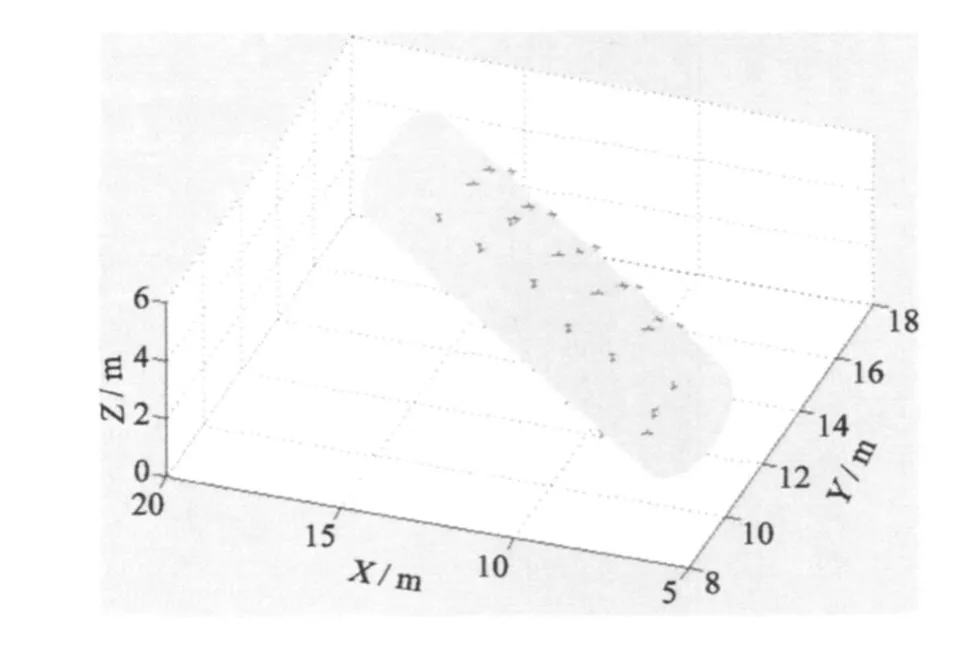
图4 拟合的椭圆柱Fig.4 Fitting of elliptical cylinder

本文提出一种可用于逆向工程中的椭圆柱构件的拟合计算方法。通过仪器采集椭圆柱构件表面的离散点,先对椭圆柱底面进行拟合,从而获得三维坐标转换参数;通过坐标转换将空间任意位置的椭圆柱转换为标准的椭圆柱;然后将椭圆柱的拟合转化为对平面椭圆的拟合,最终获得椭圆的尺寸参数。最后,将该方法应用于工程实例并取得成功,从而证明该方法是可行的。

该方法数学模型简单,便于电算程序实现。

在实际应用中,为了提高截面尺寸拟合的精度,保证计算结果的准确,可采取以下几个措施：

1)在采集构件表面点坐标时,使用高精度的仪器(例如索佳NET1200高精度全站仪),并且要尽量避免粗差的产生;

2)测量中,测站的数目应越少越好,以避免搬站或坐标归算引起的误差;

3)底面的拟合关系到坐标转换的准确度,进而影响到拟合结果,所以在采集底面点的坐标时,要注意采集点尽可能的多(最少采集 4个点的坐标),而且分布均匀;

4)侧面采集点的选取也应尽量均匀,点数应尽量的多(最少采集 6个点的坐标),可采取如本例所示的采集方法：每组采集点能形成一个平面,该平面平行于底面;而且每两组平面的距离大致相等。

1 王解先.工业测量中一种二次曲面的拟合方法[J].武汉大学学报(信息科学版),2007,(1)：47-50.(Wang Jiexian.A method for fitting of conicoid in industrial measurement[J].Geomatics and Infor mation Science ofWuhanUniversity,2007,(1)：47-50)

2 谷川.GA柱面拟合法在隧道断面收敛监测中的应用[J].大地测量与地球动力学,2010,(2)：58-62.(Gu Chuan.Application of spatial cylindrical surface fitting based on GA in tunnel section convergence monitoring[J].Journal of Geodesy and Geodynamics,2010,(2)：28-62)

3 程效军,顾孝烈.工程结构物的抛物面方程回归计算[J].同济大学学报 (自然科学版),2009,(9)：1 246-1 249. (Cheng Xiaojun and Gu Xiaolie.Regressive adjustment of paraboloid-equation for engineering construction[J].Journal of TongjiUniversity(Natural Science),2009,(9)：1 246 -1 249)

4 樊功瑜.误差理论与测量平差[M].上海：同济大学出版社,1998.(Fan Gongyu.Error theory and surveying adjustment[M].Shanghai：TongjiUniversity Press,1998)

5 潘国荣,赵鹏飞.基于空间向量的三维基准转换模型[J].大地测量与地球动力学,2009,(6)：78-82.(Pan Guorong and Zhao Pengfei.3D datum transformation model based on space vector[J].Journal of Geodesy and Geodynamics, 2010,(6)：78-82)

6 王解先,季凯敏.工业测量拟合[M].北京：测绘出版社, 2008.(Wang Jiexian and Ji Kai min.The fitting of industrial surveying[M].Beijing：Surveying andMapping Press,2008)

7 闫蓓,王斌,李媛.基于最小二乘法的椭圆拟合改进算法[J].北京航空航天大学学报,2005,(3)：295-298.(Yan Bei,Wang Bin and Li Yuan.Optimal ellipse fitting method based on least-square principle[J].Journal of Beijing University of Aeronautics and Astronautics,2005,(3)：295-298)

FITTING CALCULATION OF ELL IPTICAL CYL INDER COM PONENT IN REVERSE ENGINEERING

LeiWannan1)and Zhao Pengfei1,2)

(1)Departm ent of Surveying and Geo-Infor m atics,Tongji University,Shanghai 200092 2)Shanghai Surveying and M apping Institute,Shanghai 200063)

A method based on the principle of reverse engineering for fitting the elliptical cylinder component is proposed.At first,the data on the face of elliptical cylinder component is sampled by electronic total-station,then, the normal vector is gotten by fitting the bottom surface.At last,arbitrary elliptical cylinder is transfor med to the standard form by the coordinate transformation.In theway,the elliptical cylinder fitting transforms to the ellipse fitting.At the end,an engineering example is shown to prove the feasibility of thismethod.

elliptical cylinder component;fitting of plane;coordinate transformation;fitting of ellipse;reverse engineering

1671-5942(2010)05-0102-05

2010-04-09

雷婉南,女,1987年生,研究生在读,研究方向：精密工程测量、工业测量与测量数据处理.E-mail：leiwannanlei@163.com

P258

A