加权总体最小二乘在三维激光标靶拟合中的应用＊

陈玮娴 陈 义 袁 庆 葛旭明

(1)同济大学测量与国土信息工程系,上海 200092

2)现代工程测量国家测绘局重点实验室,上海 200092)

加权总体最小二乘在三维激光标靶拟合中的应用＊

陈玮娴1)陈 义1,2)袁 庆1)葛旭明1)

(1)同济大学测量与国土信息工程系,上海 200092

2)现代工程测量国家测绘局重点实验室,上海 200092)

针对平面标靶和球标靶拟合中最小二乘方法和总体最小二乘方法存在的问题,提出了一种加权总体最小二乘的拟合方法,根据点云激光反射强度以及对系数阵A列向量部分修正引入权阵 P、PX、P0,建立较LS方法和TLS方法更加合理的模型,并给出相应的迭代算法。经实例计算证明加权总体最小二乘方法更加合理,可以获得更高精度的参数解。

点云;EI V模型;标靶拟合;总体最小二乘;加权总体最小二乘

1 引言

标靶是由高反射率材料制成用来拟合点云特征点的反射标志,一般分为平面标靶和球标靶。在地面三维激光中它起两个作用：1)为多视点云模型的拼接提供同名公共点;2)把其他测量手段获得的控制点坐标引入到点云模型中。对于平面标靶,根据“Halo效应”,Lichti[1]等人提出求标靶平均反射强度中心来确定标靶几何中心。该估算方法基于激光扫描方向与标靶平面绝对垂直的假设。而实际常常是不垂直扫描,且当扫描方向与标靶垂直方向夹角大于 60°时会产生无法识别靶标中心的情况[2]。官云兰[3]提出稳健标靶定位方法,建立高斯-马尔科夫(G-M)模型,采用LS方法拟合平面,再进行靶心定位,可以避免不垂直扫描时产生的识别错误,但所建立的 G-M模型中未考虑到系数矩阵A的误差。对于球标靶,通常建立 G-M模型,用 LS方法拟合半个球面点云,得到球标靶的几何中心[4]。鲁铁定等人[5]提出基于 TLS方法球标靶定位方法,该方法在假定球面点云等精度获取的情况下建立的变量中的误差模型 (Error-In-Variables,EI V)[6,7]对系数阵 A和观测向量 Y进行改正[8,9],能较好地解决系数矩阵和观测向量存在误差的问题。然而在实际中,由于入射角的不同导致获取的点云激光反射强度不同,反射强度越高点位精度越高,因而拟合点云时需根据反射强度考虑每个点的拟合权重。同时系数阵A中某些固定的常数列是不需要修改的,加入权阵可以修改系数阵A的数据列,而不修改常数列。本文在官云兰的点云平面拟合和鲁铁定的球面拟合的方法基础上,引入加权总体最小二乘 (WTLS)的拟合方法,在 EI V模型的基础上根据点云激光反射强度不同的特性引入观测值权阵 P和行向量权阵 PX;根据系数矩阵A的部分列修改引入列向量权阵 P0。经实验计算,该方法能得到更加合理的模型和更高精度的参数解。

2 函数模型及解法

2.1 LS、TLS、W TLS函数模型

经预处理后得到一组标靶点云的三维坐标(xi, yi,zi),(i=1,2,…,n)。相应的空间平面方程为:

式中,a、b、c为平面参数。对于球标靶,由于从任何方向扫描均可获得半个球面点云,从点云数据中拟合球体得到球心坐标和球半径即可完成球标靶定位,相应的球面方程为:

式中,a0、b0、c0为球心坐标,r为球半径,球面方程展开形式为:

LS估计准则：

式中,Y为 n×1维观测值向量,X为m×1维待估参数,A为 n×m维的系数矩阵,e为观测向量的随机误差,In为单位阵。考虑系数矩阵 A含有误差的等权 EI V模型为：

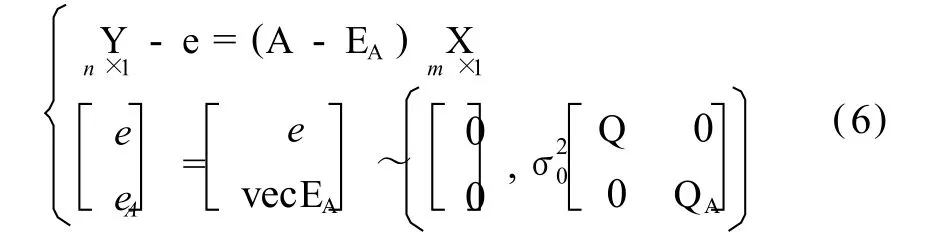
式中,EA为系数矩阵 A的随机误差,在 LS方法中EA≡0。Q=In,QA=Im⊗In=Inm,Qx=In,Q0=Im是单位权阵,“⊗”为“kronecker积”(M⊗N=[mijN], M=[mij])[10],“vec”为矩阵列向量化算子。TLS估计准则：

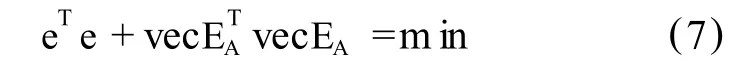
考虑系数矩阵A含有误差的加权 EI V模型：

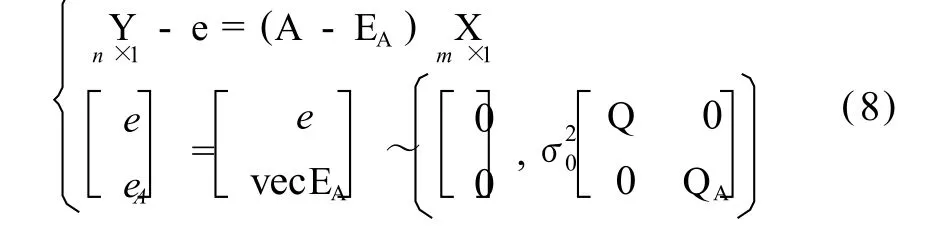
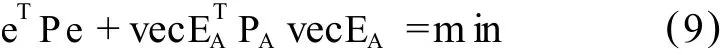
平面方程写成矩阵形式：

球面方程写成矩阵形式:

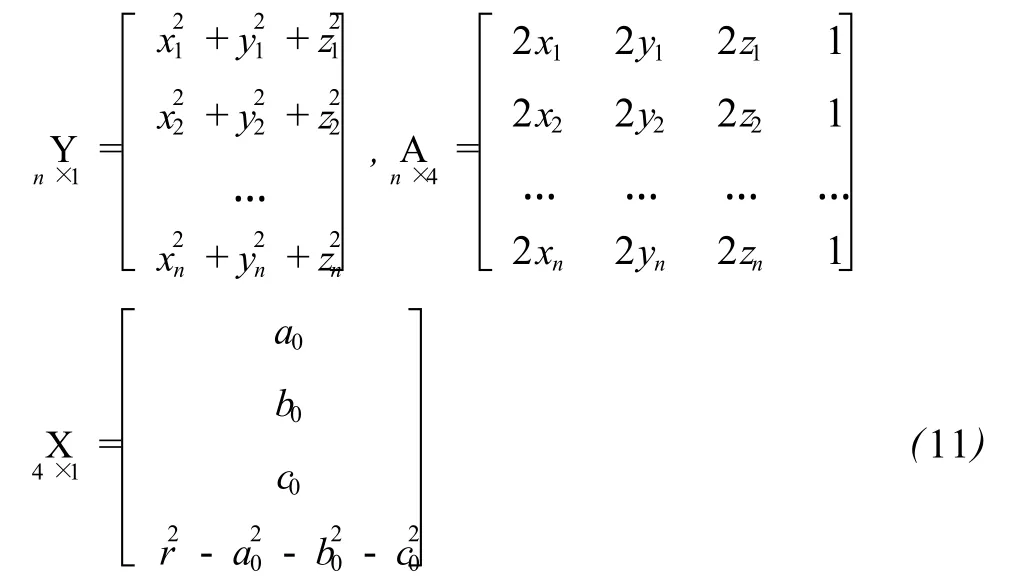
2.2 W TLS权阵的定义

图 1 激光反射强度[4]Fig.1 Laser reflection intensity[4]

假设点云在 x、y、z3个方向等精度获取。对于平面标靶的系数阵列向量和观测值,有σx=σy= σz,得到平面拟合的权阵如下:

对于球标靶,拟合模型较平面标靶复杂,根据系数阵列向量和观测值的关系,提出 3种定权方法。

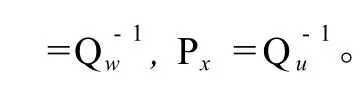
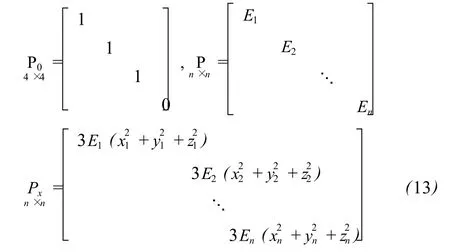
方法二:认为系数阵行向量之间等精度且与观测值向量无关,则 P0、P的形式不变,Px形式为:

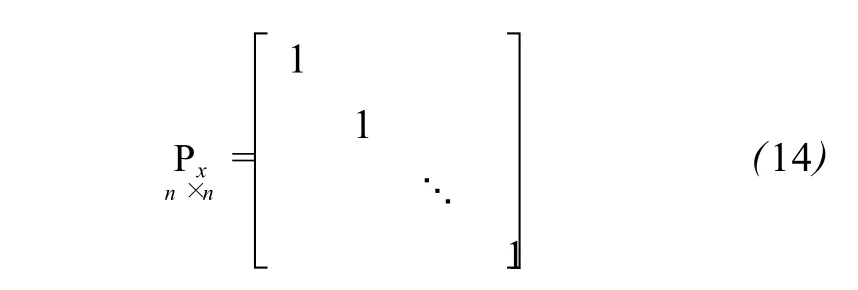
方法三:认为系数阵行向量之间权值由反射强度决定且与观测值向量无关,则 P0、P的形式不变, Px形式为:

2.3 W TLS算法及精度估计

迭代法求解过程[10-13]：

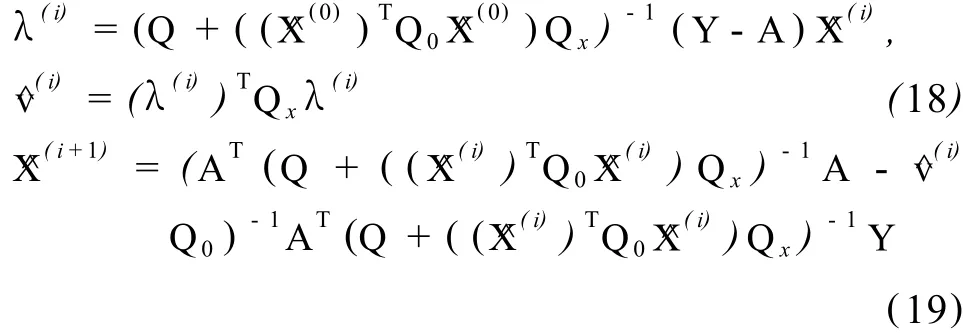
3 实例分析

采用 Faro large scanner对图 2场景进行扫描得到 3个平面标靶和 3个球标靶 (球半径设计为0.072 5 m)的点云数据。图 3是其中一个平面标靶和一个球面标靶的原始点云。手动删除大量冗余扫描点云数据,通过转换关系将每个点的反射强度转换为(0～1)之间的数值,根据标靶的反射率 0.5≤E′≤0.68设置相应阈值,消除噪声。对于平面标靶,为了避免由于直线平行与某坐标轴而出现数值问题[14],先求出 3个坐标分量的最大值和最小值Δx、Δy、Δz,再确定平面方程形式。按式 (9)组成观测方程,按式(11)组成权阵,根据式 (16)～(22)求解。对于球标靶按式(10)组成观测方程,分别按式(12)～(14)3种方法组成权阵,根据式 (16)～ (22)求解。利用上述WTLS方法求解待估参数,并与 TLS方法和LS进行比较得到的结果如表 1和表2。拟合结果如图 4和 5,观测值残差和系数阵残差如图 6,图 5(c)和图 6(f)的WTLS方法依据方法三定权。

由表 1可以看出,平面拟合中WTLS方法拟合的单位权中误差要小于 LS方法和 TLS方法,精度相对LS方法和 TLS方法平均分别提高 60.1%和57.9%。由表 2可以看出,球面拟合中 LS、TLS、WTLS方法拟合球半径与设计半径相近,WTLS方法拟合球面的单位权中误差要小于LS方法和 TLS方法,依方法三定权的WTLS方法(WTLS3)求得的精度高于方法一 (WTLS1)和方法二 (WTLS2),且WTLS3方法相对 LS方法和 TLS方法分别提高76.0%和 27.3%。由图 6(c)、(d)、(e)、(f)可以看出,TLS和WTLS方法同时改正观测值和系数阵,残差分布在观测值和系数阵中,而LS方法拟合的残差仅存在观测值中 (图 6(a)、(b))。在 TLS和WTLS方法中引入阵固定了系数阵中的常数列,即图 6(e)、(f)中系数阵常数列残差为 0。同时比较图 6(c)、(e)和 (d)、(f),可以看出WTLS方法引入阵拟合残差更好。在靶标拟合中WTLS方法建立的模型较 LS方法和 TLS方法更为合理,得到更高精度参数解。

图2 扫描场景Fig.2 Scanning scenes

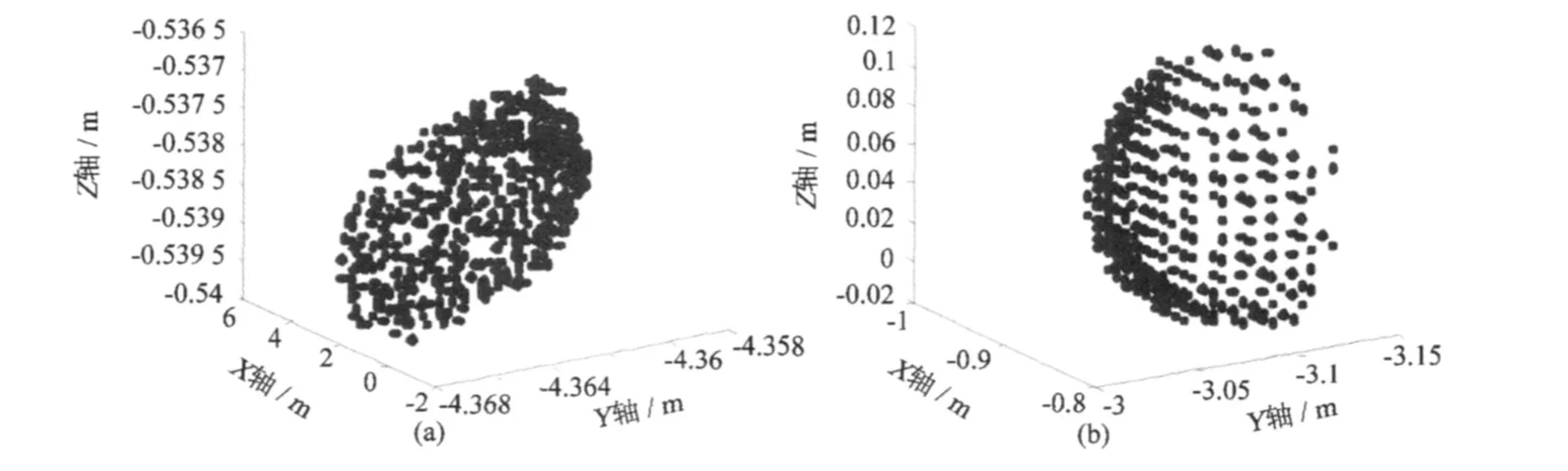
图3 平面标靶、球标靶点云Fig.3 Point cloud of plane and sphere targets

表 1 平面标靶拟合参数及精度(单位:m)Tab.1 Fitti ng results of plane targets(un it:m)

表 2 球标靶拟合参数及精度(单位:m)Tab.2 Fitti ng results of some sphere targets(un it:m)

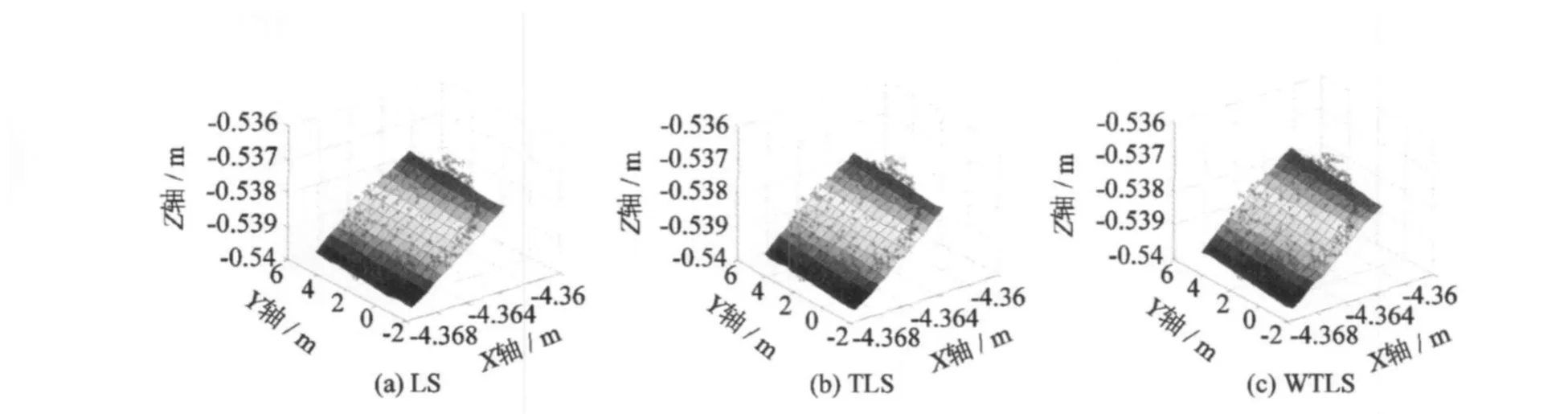
图4 平面标靶LS、TLS、WTLS方法拟合结果Fig.4 Fitting results of a plane targetswith LS、TLS andWTLSmethods

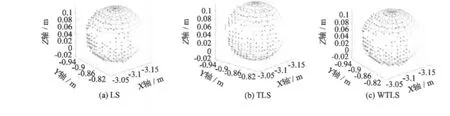
图5 球标靶LS、TLS、WTLS方法拟合结果Fig.5 Fitting results of a sphere targetwith LS、TLS andWTLSmethods

4 结语

1)在平面和球面点云拟合中,考虑到平面方程和球面方程中由实测数据组成的系数矩阵 A含有误差,从而建立 EI V模型对系数阵A和观测向量的误差同时进行最小化约束,该处理方法比认为系数阵无误差的LS处理方法更加合理。

2)在WTLS方法中引入列向量权阵,可以起到部分修改系数阵A列向量的作用,即修改A的数据列而不修改常数列,得到了更加普遍适用的模型。

3)根据每个点的激光反射强度定权,引入观测值权阵 P和系数阵行向量权阵 Px。在球标靶拟合模型中给出 P、Px3种定权方法,并加以比较。比较结果认为,合理的定权可以使WTLS方法拟合平面标靶拟合精度提高近 60%,球标靶的拟合精度较TLS方法提高近 30%,所以WTLS方法能够得到更高精度的参数解。

图6 观测值及系数阵残差Fig.6 Observations and residuals of plane and sphere targetswith LS、TLS andWTLSmethods

1 LichtiD D,et al.Benchmark tests on a three-dimensional laser scanning system[J].Geomatics Research Australasia, 2000,72：1-24.

2 朱凌.地面三维激光扫描标靶研究[J].激光杂志,2008, 29：33-35.(Zhu Ling.The research on terrestrial laser scanning target[J].Laser Journal,2008,29：33-35)

3 官云兰.地面三维激光扫描数据处理中的若干问题研究[D].同济大学,2008.(Guan Yunlan.Some problems of the processing of terrestrial laser scanning[D].Tongji University,2008)

4 张毅.地面三维激光扫描点云数据处理方法研究[D].武汉大学,2008.(Zhang Yi.Research on point cloud processing of terrestrial laser scanning[D].Wuhan University, 2008)

5 鲁铁定,等.基于整体最小二乘的地面激光扫描标靶球定位方法[J].大地测量与地球动力学,2009,(4)：102-105.(Lu Tieding,et al.Sphere target fixing of point cloud data based on TLS[J].Journal of Geodesy and Geodynamics,2009,(4)：102-105)

6 Golub H G and Van Loan F C.An analysis of the total least squares problem[J].SI AM Journal on Numerical Analysis, 1980,17(6)：883-893.

7 Chi Lun Cheng,Mastrondrdl N and Palge C.Total least squares and errors-in-variables modeling[J].Computational Statistices and Data Analysis,2007,52：1 076-1 079.

8 陈义,陆珏,郑波.总体最小二乘方法在空间后方交会中的应用[J].武汉大学报 (信息科学版),2008,32：1 271-1 274(Chen Yi,Lu Jue and Zhen Bo.Application of total least squares to resection space[J].Geomatices and Infor mation Science ofWuhan University,2008,32：1 271-1 274)

9 陆珏,陈义,郑波.总体最小二乘方法在坐标转换中的应用[J].大地测量与地球动力学,2008,(5)：77-81.(Lu Jue,Chen Yi and Zhen Bo.Applying total least squares to three-dimensional datum transformation[J].Journal of Geodesy and Geodynamics,2008,(5)：77-81)

10 魏木生.广义最小二乘问题的理论和计算[M].北京：科学出版社,2006.(Wei Musheng.Generalized total least square methods and calculation[M].Beijing：Science Press,2006)

11 Markovsky I,Huffel SVan and Kukush A.On the computation of the multivariate structured total least squares estimator[J].NumericalLinearAlgebra with Applications,2004, 11：591-608.

12 SchaffrinB andW ieserA.Onweighted total least-squares adjustment for linear regression[J].Journal of Geodesy, 2008,82：415-421.

13 Schaffrin B.A note on constrained total least-squares estimation[J].Linear Algebra and Its Applications,2006, 417：245-258.

14 王解先,季凯敏.工业测量拟合[M].北京：测绘出版社, 2008.(Wang Jiexian and Ji Kai min. Industrial measurement fitting[M].Beijing：Surveying and Mapping Press, 2008)

APPL ICATI ON OF W EIGHTED TOTAL LEAST-SQUARES TO TARGET FITTING OF THREE-D IM ENSIONAL LASER SCANNING

ChenWeixian1),Chen Yi1,2),Yuan Qing1)and Ge Xuming1)

(1)Departm ent of Surveying and Geo-Infor m atics,Tongji University,Shanghai 200092 2)Key Laboratory of M odern Engineering Surveying,SBSM,Shanghai 200092)

According to the different laser reflection intensity of each cloud point and correcting partsof the coefficientmatrixAcolumn vectors,the weighted total least-square(WTLS)methods in the plane target and sphere target fitting of the terrestrial laser scanning is introduced,a more reasonable model than the least-square(LS) methods and the total least-square(TLS)methods is established,and the corresponding iterative algorithm is given. The calculated example proves that the model ismore reasonable indeed and the more accurate parameters solution can be obtained withWTLS.

point cloud;Error-In-Variables(EI V)model;target fitting;total least-square(TLS);weighted total least-square(WTLS)

1671-5942(2010)05-0090-07

2010-05-31

陈玮娴,女,1987年生,硕士,研究方向：大地测量与测量工程专业数据处理.E-mail：15531422@qq.com

P207

A