基于小波分析的 GEO卫星异常识别研究＊

刘雁雨 常志巧 何 峰 郭 睿

(1)解放军信息工程大学测绘学院,郑州 450052 2)北京环球信息应用开发中心,北京 100094)

基于小波分析的 GEO卫星异常识别研究＊

刘雁雨1,2)常志巧2)何 峰2)郭 睿2)

(1)解放军信息工程大学测绘学院,郑州 450052 2)北京环球信息应用开发中心,北京 100094)

当卫星轨道异常发生时,用动力学方法所确定的卫星轨道与卫星实际轨道偏差较大,如不能及时发现将会严重影响用户的导航定位精度。在几何法定轨的基础上提出了基于小波分析的 GEO卫星异常识别方法,设计了固定分组法和移动开窗法两种方案,并结合 COMPASS卫星机动期间几何法定轨结果进行了分析。研究结果表明：两种方案均能准确判断卫星发生异常的时间,判定精度均优于 5 s。

地球静止轨道;COMPASS;轨道机动;小波分析;几何法定轨

1 引言

地球静止轨道 (GEO)是北斗卫星导航系统(COMPASS)的重要组成部分。但是由于各种扰动的影响,GEO卫星轨道的形状、轨道面的空间位置及卫星的星下点经度会发生变化,需要通过主动轨道控制对这些变化进行补偿,即利用星载推力器实施轨道机动[1-4]。并且,卫星运动过程中可能受到强扰动或破坏,使得卫星的位置发生突然改变或出现卫星转发器故障。

当卫星发生轨控或出现异常状况时,使用动力学方法所确定的卫星轨道与卫星实际轨道偏差较大,必须马上将其标记为不可用或切换到其他定轨方法,如不能及时发现将会严重影响用户的导航定位精度。能准确快速地判定问题发生的时间是切换定轨方法的前提,因此,有必要研究适用的算法实现GEO卫星机动快速识别并进行轨道异常的实时监测,这对于保证定轨的精度与提高导航系统的完好性有重要意义。

国外很早就开展了对空间目标在轨观测和预报的相关研究并取得成果,如,美国 XSS系列卫星具有自主在轨检查等能力,AeroAstro公司[5]提出的Escort微小卫星能够对空间目标进行在轨监视、逼近和跟踪观测,但是,具体的研究成果很少发布。近几年,国内也展开对空间目标的异常监测研究,张军[6]将目标的机动性能与 HMM模型结合对机动进行识别判断,董云峰[7,8]使用二进小波分析不同尺度下的机械能变化以判定轨道机动,华爱辉[9]提出利用测站和卫星之间的距离曲线斜率变化检测卫星机动,以上方法均能判断轨道的异常情况,但导航系统的高实时性要求对异常瞬间发现,已有方法却无法满足。

本文提出一种基于小波分析的 GEO卫星异常识别方法,在几何法定轨结果的基础上,通过对其进行小波分析,可准确快速地探测卫星轨控或发生异常状况时刻,实验采用 COMPASS卫星某次轨控期间观测数据,结果表明：该方法能够准确判断卫星机动时间,与实际机动时间仅有几秒的差异,其中移动开窗法能够在轨道机动后 5 s发现异常,发出警报。

2 GEO卫星轨道分析

目前常用的 GEO卫星定轨方法有：几何法、动力法及 Kalman滤波方法,这些方法各有优缺点[2]。其中,动力法和 Kalman滤波法都需要长时间积累数据才能达到较高的定轨精度,所得到的卫星运动轨道为平滑轨道。由于 GEO卫星机动较为频繁,而卫星机动期间,其轨道将出现较大变化,想要获得可靠的动力学轨道,必须对机动力进行有效、准确的建模[2,3],而这在实际中很难做到。而几何法定轨不受动力学模型的影响,通过实时对卫星位置进行观测,从而计算得到定轨结果,虽然较动力法及 Kalman滤波定轨法精度要低,但是在有无轨道机动的情况下,都能得到精度相对稳定的轨道信息。

利用伪距观测值进行 GEO卫星几何法定轨的误差方程可简写为：

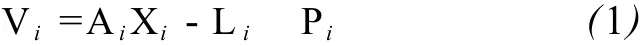
式中:Vi为第 i历元的观测值残差向量;Xi=(xi,yi, zi)为第 i历元的卫星位置改正值向量;Ai分别为位置参数的系数矩阵,其元素为伪距对坐标分量的偏导数;Li为第 i历元的观测向量;Pi为第 i历元观测值的权矩阵。

该历元的参数解可采用最小二乘估计得到:

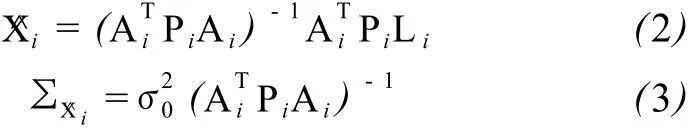
COMPASS中包含 5颗 GEO卫星,频繁地定点保持机动(约半个月一次)成为该类卫星长期管理的一项重要工作。轨道机动时,卫星的运动范围很大,可达几十千米,持续数十分钟。图 1为某次轨道机动时使用几何法定轨得到的卫星位置曲线,观测时间由 18：00：01—21：00：00,采样率为 1 s,由此次轨控的报告可知,本次实际机动为 18：27：56开始,即下图的 1 676历元处。

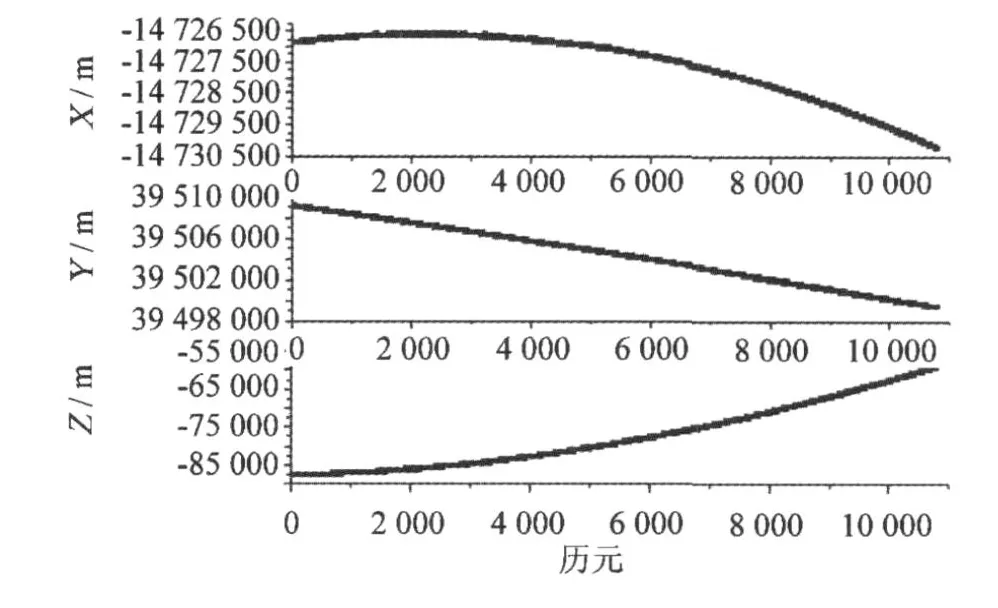
图 1 轨道机动时几何法定轨得到的卫星位置曲线Fig.1 Satellite position curve getting with geometry orbit determination method duringmaneuver period

因为几何法定轨的实时性,其定轨结果应能反映轨道机动的发生。但参照实际的机动时间可以看出,几何法定轨得到的位置曲线并未因为轨道机动受到机械推力而有明显的变换。这是因为 GEO卫星轨道机动力仅在 0.5 N～20 N之间,甚至更小,机动力对卫星产生约mm/s2量级的加速度[4],如此微小的轨道改变发生在距地面几万千米的卫星上,很难通过卫星位置的改变加以判断。

3 小波分析理论

小波分析方法是一种窗口大小固定但其形状可改变,时间窗和频率窗都可改变的时频局部化分析方法,即在低频部分具有较高的频率分辨率和较低的时间分辨率,在高频部分具有较高的时间分辨率和较低的频率分辨率。它对信号奇异性敏感的特征非常适合于非平稳信号的分析。利用小波方法进行卫星异常检测实际上是通过一定尺度上的带通滤波器对信号进行滤波,将包括特定频率成分提取出来。发生异常的位置可以看成信号中的奇异点,根据信号奇异性检测原理,来确定异常发生的时间。

对于任意的函数 f∈L2(R)的连续小波变换为

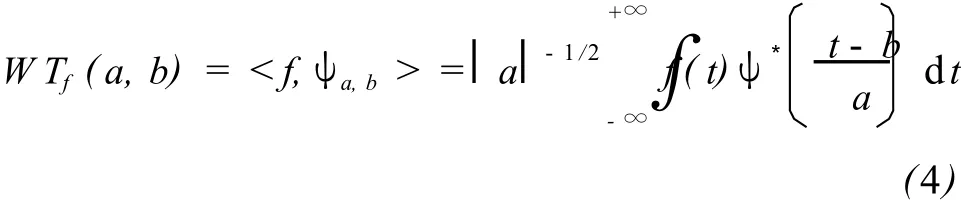
其中,ψ是基小波,a、b分别是基小波的尺度参数和平移参数[10]。

对于信号的离散正交小波变换,Mallat给出了快速金字塔算法,若 f(x)为信号的离散采样数据,令:cj=f(x),则有信号的多分辨率分析公式为:

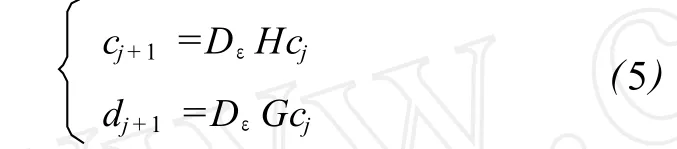
式中,cj+1为逼近信号,dj+1为细节信号,H为低通滤波器,G为带通滤波器,Dε为下抽样算子。把其中的低频部分作为信号再次分解,即可得到任意层的高频或低频分量。

4 基于小波分析的 GEO卫星异常识别研究

因为小波变换具有空间局部化性质,因此,利用小波变换来分析信号的奇异性、奇异性位置和奇异度的大小是比较有效的。本文也据此构造了基于小波分析的 GEO卫星异常识别方法：1)对 GEO卫星进行几何法轨道确定;2)使用合适的小波基对卫星轨道做小波分析;3)通过设定阈值探测 GEO卫星的机动时刻。

具体的探测方案为固定分组法和移动开窗法。

由图 2、3、4可以看出,在卫星轨道的小波分解中,第三层 (d3)和第四层 (d4)的高频部分中信号的高噪声部分显示得相当明显,这是因为如将卫星正常工作时计算得到的轨道视为一蠕变信号,那么当卫星发生机动等异常情况时,计算得到的轨道将会出现突变信号(主要表现在幅度和频率的突变),通过对信号进行多尺度分析,在信号出现突变时,其小波变换后的系数具有模量极大值,因而可以通过对d3或 d4的检测来确定故障发生的时间。

抽取测得的非机动时间连续 n个几何法定轨结果作为样本,对其进行小波分解得到其高频分量d4,求出采样值的均值和采样值的标准差δ,即

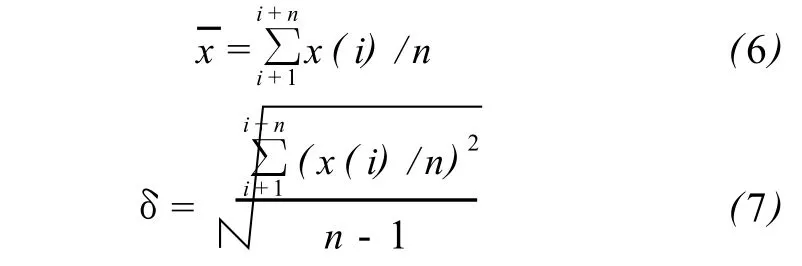
固定分组法:以 3δ作为先验阈值,将观测数据分为m组,求出各组标准差,大于 3δ即认定为卫星发生机动。

移动开窗法:以 3δ作为先验阈值,设窗口宽度为m,由起始历元开始,窗口依次向后平移,求各窗口标准差,大于 3δ即认定为卫星发生机动。

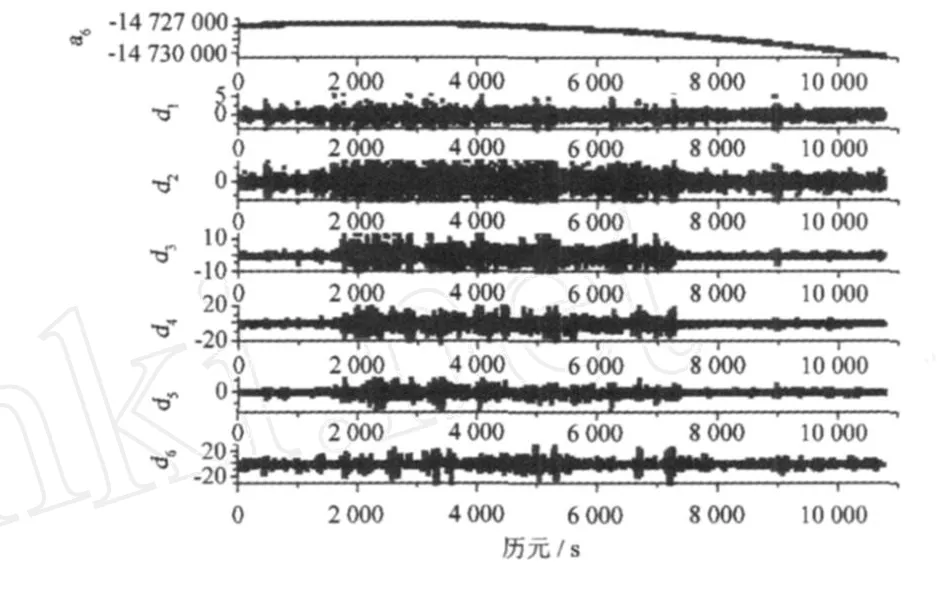
图 2 用 db3小波将卫星 X方向分解 6层:X=a6+d1+ d2+d3+d4+d5+d6Fig.2 Satellite’sXaxis is deposed to six levels by db3 wavelet：X=a6+d1+d2+d3+d4+d5+d6

图 3 用 db3小波将卫星 Y方向分解 6层:Y=a6+d1+ d2+d3+d4+d5+d6Fig.3 Satellite’sYaxis is deposed to six levels by db3 wavelet：Y=a6+d1+d2+d3+d4+d5+d6

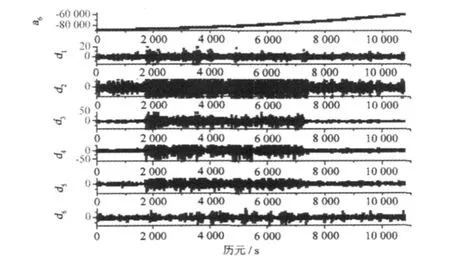
图 4 用 db3小波将卫星 Z方向分解 6层:Z=a6+d1+ d2+d3+d4+d5+d6Fig.4 Satellite’sZaxis is deposed to six levels by db3 wavelet：Z=a6+d1+d2+d3+d4+d5+d6

以所述的COMPASS系统某 GEO卫星采样率为 1 s的数据为例,取非机动时的 100个观测数据作为样本进行几何法定轨,对其小波分解得到的高频分量 d4进行探测,计算得到其 3δ作为阈值。

方案一:采用固定分组法,将观测数据使用 db3小波进行分解,得到的 d4序列每 10个一组,计算其标准差,如某组标准差大于 3δ,则认定这一组的第一个历元即为轨控开始时刻。

方案二:采用移动开窗法,将观测数据使用 db3小波进行分解,得到其 d4序列,设定窗口宽度为 10 s,由起始历元开始,依次后移,计算其标准差,如某组标准差大于 3δ,则认定这一组的第一个历元即为轨控开始时刻。

表1为对几何法定轨X、Y、Z3方向分别进行机动探测得到的结果。

表 1 机动时刻测定值Tab.1 M easured values of orbitmaneuver ti me

由表 1可以看出,使用两种方案对三轴方向分别检测得到的卫星机动开始时间均互相吻合,并且与实际机动时间极其接近。

在方案一中,机动检验的分辨率主要受分组m的影响,因为 GEO卫星几何结构差,如观测值含粗差,对其几何法定轨结果影响明显,较大的 m可以对几何法轨道中的噪声进行平滑,但会影响对机动时间的精确判断;m太小,又无法消除几何法定轨中观测数据存在的噪声对机动探测的影响,容易引起误判。但方案一存在轨控开始的几个历元落入某一分组中但该分组的标准差仍不能超过阈值的可能性,这将导致直到下一分组计算完毕,才能发出报警。在方案二中,机动检验的分辨率同样受到分组m的影响,但避免了方案一的分组位置固定所造成的报警延后缺陷。在报警的及时性方面,使用固定分组法能够在轨道机动后 14 s发出警报,使用移动开窗法能够在轨道机动后 5 s即发出警报。

5 结论

为实现 GEO卫星机动的快速识别并进行轨道异常的实时监测,对卫星发生异常时刻的检测方法进行了初步探讨,提出了基于小波分析的 GEO卫星异常识别方法,并设计了两种方案：固定分组法和移动开窗法。两种方案均能够快速准确的检测到卫星的异常状况,而且无需积累大量数据,能够实现近实时快速计算检测。

通过对COMPASS系统中某 GEO卫星的实测数据进行分析,结果表明：两种方案均能够快速准确地检测到卫星的异常状况,其判定精度均优于 5 s。但移动开窗法的实时性更佳,在异常发生后 5 s时即能发出警报。

1 GrewalM.Comparison of GEO and GPS orbit determination [M].Portland,2002.

2 刘林.航天器轨道理论 [M].北京：国防工业出版社, 2000.(Liu Lin.Spacecraft orbital theory[M].Beijing：Defense Industry Public House,2000)

3 杜兰.GEO卫星精密定轨技术研究[D].信息工程大学, 2006.(Du Lan.A study of the precise orbit determination of geostationary satellites[D].Infor mation and Engineering U-niversity,2006)

4 JOSE M,et al.Station keeping maneuvers for geostationary satellites using feedback control techniques[J].Aerospace Science and Technology,2007,11(2)：229-237.

5 车汝才,张洪华.追踪星跟踪空间非合作目标的相对轨道设计[J].航天控制,2006,24(5)：40-45.(Che Rucai and Zhang Honghua.Relative orbit design of space tracking satellite tracking non-cooperative target[J].Astronautic Control, 2006,24(5)：40-45)

6 张军,等.基于HMM的机动目标识别[J].国防科技大学学报,2003,25(2)：51-55.(Zhang Jun,et al.Moving target recognition based on HMM[J].Journal ofNationalU-niversity ofDefense Technology,2003,25(2)：51-55)

7 董云峰,苏建敏.利用小波分析识别空间目标的轨道机动[J].宇航学报,2004,25(2)：213-218.(Dong Yunfeng and Su Jianmin.Detection of space target orbitmaneuver by wavelet analysis[J].Journal of Astronautics,2004,25(2)：213-218)

8 张振军,董云峰.基于小波分析的目标轨道机动自主检测方法[J].北京航空航天大学学报,2008,34(3)：353-356.(Zhang Zhenjun and Dong Yunfeng.Autonomic detection method of space tartget orbitmaneuver based on wavelet analysis[J].Journal ofBeijingUniversity ofAeronautics and Astronautics,2008,34(3)：353-356)

9 华爱辉,等.基于转发式测轨系统的 GEO卫星机动检测初探[J].时间频率学报,2007,30(2)：118-223.(Hua Aihui,et al.A menthod to monitor geostationary satellite maneuver based on orbit measuring system with transponder [J].Journal of Ti me Frequency,2007,30(2)：118-223)

10 胡昌华,张军波.基于MATLAB的系统分析与设计——小波分析[M].西安：西安电子科技出版社,2000.(Hu Changhua and Zhang junbo.System analysis and design base onMATLAB——wavelet analysis[M].Xi’an：Xi’an Electronic Science and Technology Public House,2000)

GEO SATELL ITE ABNORM ITY RECOGNITION BASED ONWAVELET ANALYSIS

Liu Yanyu1,2),Chang Zhiqiao2),He Feng2)and Guo Rui2)

(1)Institute of Surveying and M apping,Infor m ation and Engineering University,Zhengzhou 450052 2)B eijing Global Infor m ation Center of Application and Exploration,Beijing 100094)

Satellite orbit gettingwith the dynamic deter mination method is significantly biased from its real position at the occurrence of satellite orbit abnormity,which will lead to serious influence on the positioning accuracy of the users.A method with wavelet analysis technique based on geometric orbit deter mination for GEO satellite abnormity recognition is proposed and then the grouping fixedly scheme and the openingwindow scheme are designed for dealingwith the geometric orbit determination results during the COMPASS satellitemaneuverperiod.According to the analysis results,both kinds of scheme can distinguish the happening time of satellite abnor mity exactly and the resolution is better than five seconds.

Geostationary(GEO);COMPASS;orbitmaneuver;wavelet analysis;geometry orbit determination

1671-5942(2010)05-0073-04

2010-03-13

上海空间导航与定位技术重点实验室基金 (06DZ22101);武汉大学卫星导航与定位教育部重点实验室基金 (GRC-2009004);国家“863”计划项目(2009AA12Z328)

刘雁雨,女,1980年生,博士研究生,工程师,从事卫星导航定位研究.E-mail：liu_yanyu@hotmail.com

P228.1

A