最大输沙率法推求石马河稳定河宽

杨胜发，袁观栋，罗羚源，胡鹏飞

(重庆交通大学河海学院，重庆400074)

航道整治工程中经常遇到确定整治河段岸线问题，即稳定河宽问题。通常运用最大法输沙率和稳定河槽宽度法，笔者采用最大法输沙率推求稳定河宽。通过稳定河宽的确定为河道的整治提供最优方案。

石马河位于重庆市奉节县草堂镇，距长江入汇口(白帝城附近)6.5 km，属于大比降卵石河流，在洪水期流量、流速和比降均较大，并且有部分弯曲河段。石马河河道治理工程是草堂镇场镇规划及工业园区建设的重要组成部分，若堤防的防护措施考虑不当，将很容易造成其水毁，保持工程河段稳定的河床宽度是保证河段稳定的关键。

1 石马河河段基本特征

石马河为三峡库区长江北岸的一条支流，属典型的山区河流。工程河段尾部以上控制流域面积184 km2，河道全长 19.2 km，河道平均比降 31.4‰。工程段50 a一遇流量为1 170m3/s，暴雨时期洪水具有涨水快(5h左右)，持续时间短(2～3h时左右)，退水时间长(15h以上)的特点。

石马河为典型的大比降卵砾石河流，河岸局部有基岩控制，河床组成主要为卵砾石和漂石。在最近20多年内，未出现大的暴雨洪水，河床变化不明显。

2 河床宽度与输沙率3种观点

在已知流量、河床组成、河道比降情况下，河道输沙率与河宽的关系目前有3种观点:①输沙量随着宽度的减少而增加(Henderson［1］);②输沙量随着宽度的增加而增加(Bagnold［2］，Parker［3］);③前 2种形式都存在，在某个特殊的宽度输沙率有一个最大值(Gilbert［4］)。通过分析目前的 3种观点，都存在一定的缺陷。

Henderson假设单宽推移质输沙量qs与单宽流量q是简单的指数关系，即:

断面总输沙量为Qs与流量的关系Q:

式中:B为河槽宽度。

当k＞1时，输沙量随宽度的减小而增加。Henderson根据 Einstein［5］推移质输沙率公式，认为k=2。

Henderson方法中Einstein公式不是简单的指数公式，在不同水流强度时k值不一样。直接令k=2，通过式(1)推断输沙量随宽度变化的趋势得到的结果不可靠。

Parker针对卵砾石河流，推导了断面输沙量与宽度的关系。在水流条件与起动拖曳力相比相差不大时，单宽输沙量、单宽流量与水深有如下关系:

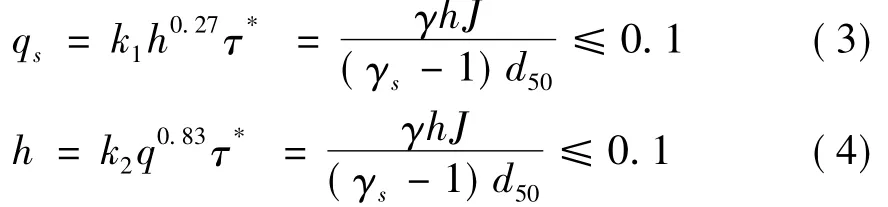
通过式(3)和式(4)可以得到:

Parker主要限制条件是水流条件强度不大，泥沙运动强度较弱，床面阻力主要是定床阻力，可得到式(3)和式(4)。对于水流条件强度较大，泥沙运动强度较强，床面有沙波运动，得出的关系与式(3)和式(4)有所出入。对于卵砾石河流来说，式(5)不能代表所有水流强度情况下的输沙量方程。

Michael［6］根据输沙率公式的特征，断面输沙量表达成如下形式:

对式(6)求导，

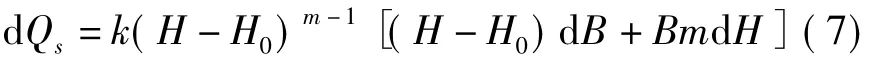
根据谢才－曼宁公式:

对式(9)求导，

将式(10)代入式(7):

将式(12)代入式(6)可得到最大输沙率对应的宽度。

Michael［6］在最大输沙率对应的宽度的分析中有以下问题未加以考虑:

1)未划分河床阻力河岸阻力。在相同流量下，河床宽度较小时，水深较大，河岸阻力较大。如不考虑河岸阻力得到的剪切力偏大;

2)河床输沙强度不同，其糙率(阻力)不是常数，应考虑动床阻力。

3 本文方法推求最大输沙率的宽度

在流量一定的情况下，最大输沙率对应的宽度可能的3种情况皆因选择的输沙率公式和假设条件不同而得到的。对于大比降卵砾石河流，主要是河道的水力计算和输沙率公式的选择。

3.1 河道水力计算

已知流量Q、河床比降J和河床组成，假设水深为H，形状为矩形，河岸糙率nw。

1)计算Rb

由谢才－曼宁公式计算出河床的综合糙率n:

根据Einstein将综合阻力划分为河岸阻力和河床阻力的方法，计算出nb和Rb:

2)计算沙粒阻力(R'b)

Einstein and Barbarossa推荐对数流速公式计算R'b:

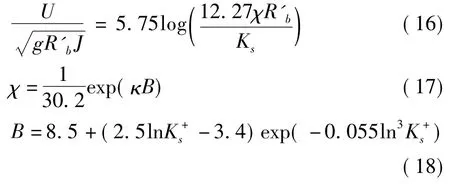
3)沙波阻力(R″b)

采用杨胜发［7］等研究明渠动床的沙波阻力方法，当相对光滑度h/d65＜150时，沙波阻力与h/d65有关，经回归分析提出了计算沙波阻力的公式:

低能态:高能态:

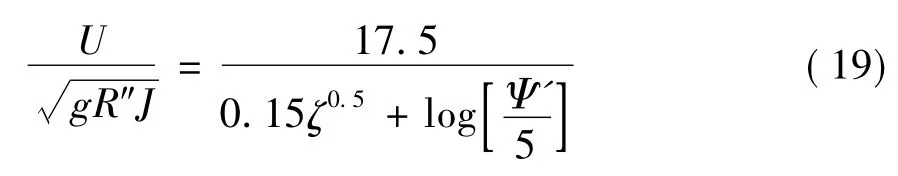
按照上式可计算出R″b。

4)判断Rb(第1步计算)是否等于(第2、3步计算)，如不相等，重新假设H，重复1)～4)步。

3.2 床面有效切应力计算

流量一定，随着河床宽度B减小，水深H增加，宽深比B/H减小。宽深比B/H小到一定程度时，河床阻力受到边壁的影响。Cao［8］分析了宽深比对床面有效切应力的影响:

3 .3 输沙率计算

笔者选取 Ackres 和 White［9］，Einstein 修正式［10］，Meyer－Peter公式［5］进行计算和分析。

水流强度:

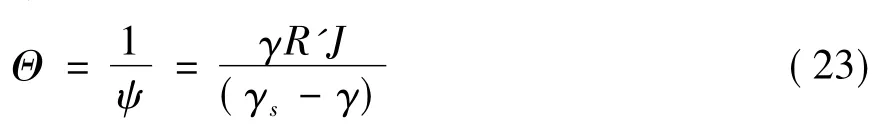
输沙强度:

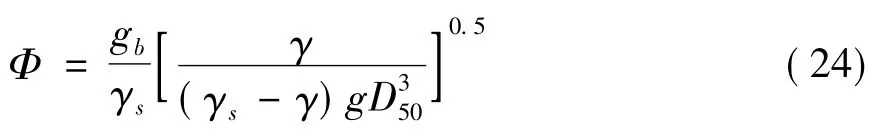
Ackres和 White 式［9］:Einstein 修正式［10］:

4 石马河最大输沙率的宽度计算结果与分析

石马河河道治理工程的标准使用年限为50 a，防洪标准为50 a一遇洪水，因此研究石马河来流的洪水控制流量为50 a一遇洪水(Q50=1 170m3/s)。石马河控制流量、比降、河床级配组成以及边壁糙率作为不同宽度输沙率计算的初始条件见表1。按照本文的计算方法，计算出石马河不同宽度的输沙量见表2。

表1 石马河输沙率计算初始条件Tab.1 Initial conditions of sediment transportrate ratecalculation of the Shima River

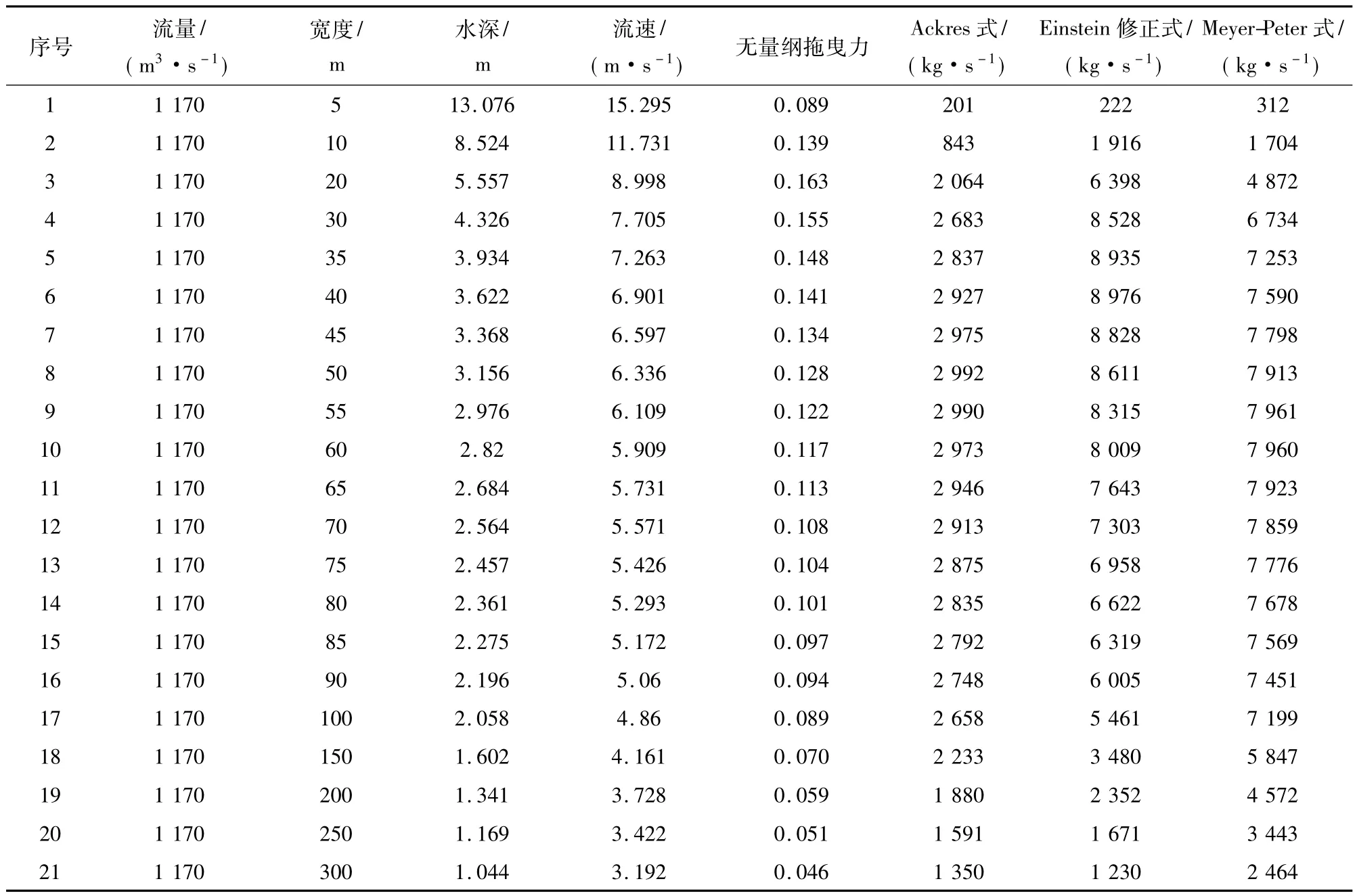
表2 石马河不同宽度的输沙率Tab.2 Sediment transport rate of different width of the Shima River

为了使计算结果更直观，将表格数据图表化，对比3种输沙强度公式下输沙率与宽度的关系，以及各公式输沙率比率与宽度关系，详情如图1～图2。

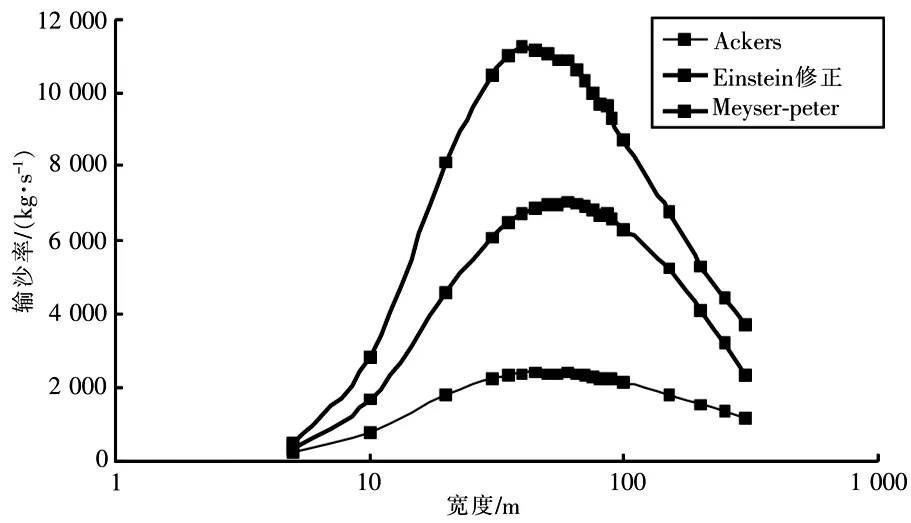
图1 各公式输沙率与宽度的关系Fig.1 Relation between caculation sediment transport rateand width according to different formula

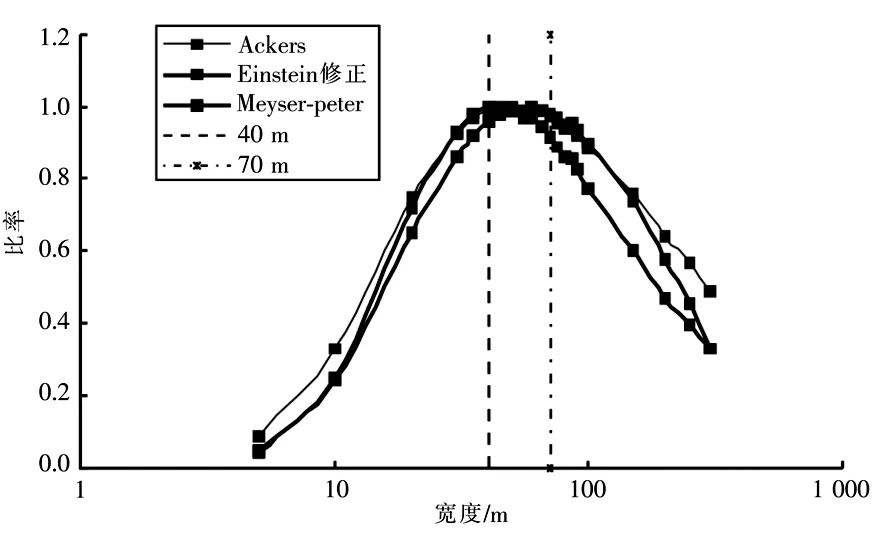
图2 各公式输沙率比率与宽度的关系Fig.2 Relation between sediment transport rate and width according to different formula

计算结果显示，采用不同的输沙率公式，皆可得到相同的规律:在流量一定的情况下，在宽度较小时，输沙率随着宽度的增加而增减，当达到某一宽度时，输沙率最大，最后随着宽度的增加，断面输沙率减小。

总的来看，在宽度为40～70m，各公式计算的输沙率是最大输沙率的96%以上。在宽度为40～70m时，水深为 2.56～3.62m;断面平均流速为5.5 ～6.9m/s;无量纲拖曳力为 0.10 ～0.14。采用不同的输沙率公式，最大输沙率对应的宽度有所变化，Ackres、Einstein修正式和 Meyer－Peter公式计算的最大输沙率对应的宽度分别为45，40和60m。按照最大输沙率对应的石马河河槽宽度为40～70m。

5 物理模型实验结果

物理模型布置了30，40，60，80m共4种河宽，在保持来流条件一致的情况下，分析了河段内冲刷深度与宽度、河道水深、流速以及河段冲淤情况等等，重点分析了输沙量和河道最大冲淤高度与面积。

总结物模实验结果，30m河宽整体冲淤较平衡，局部冲刷较大;40m河宽冲刷尺度与30m相差不大，但水深较小，整体冲刷量小;60m整体都处于弱于状态;80m冲刷尺度很大。综合分析实验结果提出40m+60m方案，采用整治河段进口为60m河宽，下游为40m河宽，整体冲淤较理想。

6 结语

在对石马河工程河段基本资料分析的基础上，对比目前输沙率与稳定河宽的几种观点，提出最大输沙率的稳定河宽方法，利用数学推导法推求河道的水力计算和输沙率公式，结合物理模型实验进行验证计算得出输沙率与河道宽度的基本规律:在流量、河床比降、河床组成一定的情况下，开始阶段输沙率随宽度的增加而增加，当宽度达到一个最大值后，随宽度进一步增大，输沙率反而减小。分析大量计算结果，将其量化为直观的图标形式，最终确定最大输沙率对应的石马河河槽宽度为40～70m。

物理模型实验采用4种不同的河宽，在来流条件一致的情况下，测量了冲淤尺度、水深、流速等参数，重点分析整治河段冲淤情况，最终得出40m+60m的实验方案。

数学推导结果和物模实验结果基本一致，故利用最大输沙率法推求稳定河宽的研究成果可应用于指导石马河河道治理工程。

［1］Henderson F M.Open channel flow［M］.New York:MacMillan Publishing Co.，1996.

［2］Bagnold R A.Bedload transport by natural river［J］.Water Resour，1979，13(2):303 －312.

［3］Parker G.Hydraulic geometryof active gravel river［J］.Hydr Div，1979，105(9):1185－1201.

［4］Gilbert G K.The transportation of debris by running water［M］.Washington，D.C.:U S Government Printing Office，1994.

［5］钱宁，万兆惠.泥沙运动力学［M］.北京:科学出版社，2003.

［6］Michacel A C，George A G.Influence of channel width on bed load transport capacity［J］.Hydr Div，1988，113(12):1489 －1509.

［7］杨胜发，周华君，胡江.内流河宽浅变迁河段水沙运动规律研究［M］.重庆:重庆大学出版社，2007.

［8］Cao S，Knight D.Design for hydraulic geometry of alluvial channels［J］.Journal of Hydraulic Engineering，1998，124(5):484－492.

［9］Ackers P，White R.Sediment transport-new apporach and analysis［J］.Journal of the Hydraulics Division，1973，99(11):2041 －2060.

［10］王兴奎.河流动力学［M］.北京:科学出版社，2007.