基于动力特性的拱桥加固效果评价

2010-11-09周建庭杨建喜孙虹微

重庆交通大学学报(自然科学版) 2010年6期

陈悦，周建庭，杨建喜，孙虹微

(重庆交通大学，重庆400074)

西部地区幅员辽阔，因其地理形势的特殊性，拱桥数量众多。在长期运营和环境变化等因素的影响下，修建的不少拱桥出现了各种各样的病害，需要进行加固处治。然而，目前对加固效果的评价还没有形成统一的标准，众多学者从承载能力、耐久性和最小应变能等方面进行评估，或者运用层次分析法和可靠度理论来度量［1－4］，这些方法对加固效果的反应均不够敏感且分析过程较为繁杂。由于加固后桥梁结构的变化，会导致结构刚度和柔度等物理参数的变化，进而引起结构动力特性的改变，如:自振频率和振型的改变［5］。同时，动力特性分析能较方便地获得桥梁结构整体的加固效果信息，且反应较敏感。鉴于此，笔者在刚度分析的基础上进一步提出基于频率的拱桥加固效果评价方法，并结合工程实例予以验证，结果表明了频率评价方法的有效性及可行性。

1 基于刚度的拱桥加固效果评价方法

加固增强使得原结构成为二次受力结构，原有主拱圈是在已有变形基础上承担部分恒载和活载的，在外荷载一定的情况下影响承重构件内力的主要因素有:①偏离弯矩(恒载压力线与拱轴线偏离产生的);②弹性压缩。因此，为了增强拱桥的加固效果，尽量减小恒载压力线与拱轴线偏离显得尤为重要。

在挠曲线方程一般表达形式的基础上，结合加固处治是二次受力结构，设主拱圈在加固后的挠曲线方程为:

式中:1/ρ为主拱圈加固后挠曲线曲率;y为主拱圈加固后挠曲线;M1、EI1为主拱圈加固前受到的弯矩(恒载产生)和平面内的抗弯刚度;M2、EI2为主拱圈加固后受到的弯矩(新增部分及活载作用)和平面内的抗弯刚度。

由式(1)可知，加固后的挠曲线与恒载压力线能否更好的重合，与加固前后主拱圈截面弯矩和平面抗弯刚度密切相关。

在实际工程中，为了能更加清楚地了解加固结构物变形情况，往往以挠度来进行度量。挠度分恒载挠度与活载挠度，前者是由结构自重引起的竖向变形;后者是由活载引起的竖向变形，活载离去后这种变形就消失。目前对于加固增强后的桥梁，依据总挠度变化率βT［6－7］对评价加固的效果有重要意义，其表达式如下:

式中:βT为加固后某个观测点的总挠度变化率;δ0为加固前结构在全部荷载(含恒载和活载)作用下某个测点挠度值;δ2为加固后与δ0对应的结构相应测点挠度代表值。

挠度评价方法中的βT是从“宏观”上分析得到的一个能清楚、直观反映加固后结构挠度变化的参数。若从刚度提高这个角度而言，一个优秀的拱桥加固工程应该满足βT＜0，即:加固后拱桥的刚度宜有所增加(或者在全部荷载作用下挠度宜有所减小)。但是，要想全面了解拱桥加固处治的效果，用来作为评价测点的数目非常多才能得到满意的结果。因此，在刚度评价基础上寻求一种方便、全面、行之有效地评价拱桥加固处治效果的方法显得尤为重要。

2 基于动力特性的拱桥加固效果评价原理与方法

通常工程结构体积大，构件多，且常有隐蔽部分。因此，对加固桥梁来说静态指标的评价工作量大，且只能获得结构的局部加固效果信息。而基于动力特性的分析可以弥补静态指标的不足，能较方便地获得桥梁结构整体的加固效果信息。常用的动力特性有:频率、振型、振型曲率等。在实际评价分析中，考虑到频率具有以下优点:①最易得到的结构动力特性;②依靠当前技术测量的最准确的结构动力特性。在低阻尼情况下结构动力识别的分辨率一般可达0.1%，故把频率作为本文拱桥加固效果评价的动力特性。

在实际的计算过程中，要精确求解拱的固有振型，即使对于圆弧拱或抛物线拱这类简单拱轴线形也是很困难的。但是，拱的固有振动分析是一个特征值问题，振型的近似性不会给其对应的频率(特征值)带来很大影响。瑞雷－李兹法求解拱桥频率的近似公式如下:

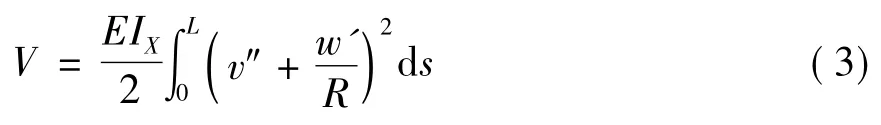
1)拱在平面内振动时的位能为:式中:EIX为拱截面在拱平面内的抗弯刚度;v(s，t)为拱轴径向位移;w(s，t)为拱轴切向位移;L为拱弧轴线的全长;R为拱轴线形。

若引入振动时拱轴线不变形的假设，即令ω'－v/R=0，则式(3)可改写为:

2)拱在平面内振动时的动能为:

根据瑞雷法原理Vmax=Tmax，由式(4)和式(5)得到频率计算公式:

由式(6)可知，拱桥频率ω是结构整体刚度和整体质量的函数，是一个整体量。

通过上述分析不难得到，经加固处治后引起拱桥某些结构刚度和质量的变化，会导致结构整体固有频率的改变，在进行效果评价时不需要大量的测点信息。同时，考虑到动力特性的分析在评价方面优于静态指标，动力特性频率拥有众多的优点，再结合频率评价方法比刚度评价方法更全面反应加固效果信息，且计算工作量少的特点，容易得出基于动力特性频率能更好的对拱桥加固效果进行评价的结论。

但值得注意的是，计算出来的频率精度跟设定的v(s，t)拱轴径向位移和w(s，t)拱轴切向位移有关，为了尽可能地接近精确值应减少附加约束的影响［8］。

3 工程实例

3.1 工程概况

实例1:红旗桥位于重庆市铜梁县境内，为单跨实腹式石拱桥。桥全长20.0m，桥跨布置为1×净10.0m，净矢高 3.25m，矢跨比 1/3，主拱圈厚度0.6m，其宽为8.5m。上部桥面布置为:1.8m人行道+9m行车道+1.8m人行道。主拱出现一条纵向裂缝，宽度约为8～10 mm，深度约为5 cm，在纵向近似贯穿整个主拱圈，横向距最近边缘1/3拱圈宽度。

实例2:水磨大桥位于重庆市开县境内天和—矿家湾线路上，为单跨空腹式石拱桥。桥全长37.0m;主拱圈净跨径 31.0m，净矢高 5.3m，厚度 0.9m，宽为6.7m;腹拱圈净跨径 3.25m，净矢高 1.2m，厚度0.25m，其宽为6.7m。上部桥面布置:0.3m栏杆+6.1m行车道+0.3m栏杆。腹拱圈拱腹开裂严重，每跨均有1～2条纵向贯穿裂缝，宽度约为7～9 mm，深度约为3 cm，在桥梁中心线或距边缘50 cm处;桥面破损严重。

红旗桥与水磨大桥的加固处治方案如表1。

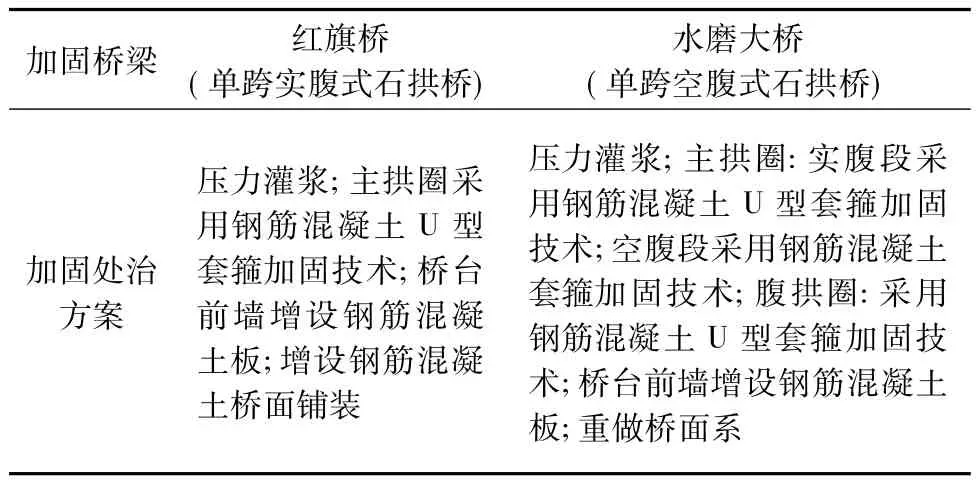
表1 桥梁的加固处治技术方案Tab.1 Strengthening treatment technology for bridges

3.2 常规刚度评价方法

建模计算时，红旗桥与水磨大桥纵向均划分16个单元(即17个节点);加固前主拱圈开裂，根据提供的裂缝宽度和深度，采用折减后的截面特性作为建模时的截面特性;由于采用压力灌浆技术，加固后对裂缝不作特殊处理。红旗桥和水磨大桥加固前后主拱圈各个节点的挠度绘制成曲线如图1和图2。

图1 红旗桥加固前后挠度变化Fig.1 Deflection change of the Hongqi Bridge before and after strenghtening

图2 水磨大桥加固前后挠度变化Fig.2 Deflection change of the Shuimo Bridge before and after strengthening

依据总挠度变化率βT来评价加固效果(表2)。

表2 总挠度变化率βT计算Tab.2 Calculation of the change rate for total deflection βT

3.3 动力特性频率评价方法

为了得到频率值，加固前后均采用 MIDAS/CIVIL结构软件建立平面梁单元模型来进行计算。红旗桥建模时，拱脚约束采用固结，且未计拱上建筑的影响，拱上建筑的恒载经过折算用梯形荷载来模拟，所有的计算分析都是在裸拱的基础上完成的;水磨大桥则是除主拱圈之外，还模拟了拱上立柱及腹拱圈，其余拱上建筑的恒载经折算同样用梯形荷载来模拟，边界支承条件均采用固结方式，立柱与主拱、腹拱与立柱之间采用刚性连接;对裂缝的处理与常规刚度方法中的相同。计算中用子空间迭代法分析特征值，迭代20次，收敛误差为1×e－10，加固前后频率值见表3。

表3 加固前后计算频率对照Tab.3 Comparison between calculated frequencies before and after strengthening

3.4 分析

由表2和表3对比分析可知，通过刚度对加固效果进行评价，只能获得局部的加固效果信息，若要全面、详细地了解拱桥结构各部分的状态变化，则计算繁琐、工作量大;然而，基于结构动力特性的频率能较方便地获得拱桥结构整体的加固效果信息，且具有反应较敏感的特点，因此证实了依据结构频率可以评价拱桥的加固效果，并且评价效果良好。