数学建模思想方法融入高等数学教学的思考与实践
2010-11-07杨曙光李治明
杨曙光, 李治明
(新疆大学数学与系统科学学院 ,乌鲁木齐 830046)
数学建模思想方法融入高等数学教学的思考与实践
杨曙光, 李治明
(新疆大学数学与系统科学学院 ,乌鲁木齐 830046)
通过对若干高等数学应用问题教学过程的分析展示,着意讨论了通过还原应用问题的真实与生动,创设情境以激发探究,将实际问题转化为数学问题的过程;提供了立足课本,把握数学建模的关键环节,使学生了解数学建模思想方法及步骤、提高“用数学”能力的实践方案;说明把数学建模的思想方法积极渗透、有机融合到公共数学课程中是可行和有效的.
高等数学; 应用问题 ;数学建模; 思想; 方法
克莱茵曾说:“逻辑关系或可以说数学机体上的硬骨架,必须保持下去,以便使数学具有它特有的可信性.数学的生命,数学最重要的动力,数学在各方面的作用,却完全依赖于应用,即取决于那些纯逻辑内容和其他一切领域间的相互关系”.“数学建模”及“数学实验”类课程的开设,正是这一观点在数学教育实践中的具体体现.所谓数学模型是指通过抽象和简化,使用数学语言对实际现象的一个近似的刻画,以便于人们更深刻地认识所研究的对象.数学建模思想方法的本质,是将实际问题转化为数学问题;而实现问题转化的关键环节,是通过对实际问题的抽象、简化,做出必要、合理、恰当的假设,以提出数学内涵,建立数学模型.首先建模时究竟该保留实际问题的什么因素,忽略什么因素并没有什么范式可依循,需要建模者根据对实际问题的理解、研究的目的以及数学背景进行归纳提炼加工,去粗取精、去伪存真来完成,这是一个创造性的过程;最后,还要将分析模型所得到的数学结论回到实际中去解释问题,以检验所得数学模型是否符合实际问题,进而解决问题,这同样是一个创造性的过程.这是数学建模的难点,也可能成为提高学生“用数学”能力的契机.
李大潜院士在“2008年大学数学课程报告论坛”上所作的《漫谈大学数学教学的目标与方法》报告中谈到,学习数学这门学科(无论是对中小学还是对大学,无论是对理工科还是对文科,无论是对青少年还是对成人,无论是将来走上怎样的工作岗位,)应该努力达到三个方面的要求,简而言之就是知识、能力、素养和精神.李院士指出:“如果割断了数学与外部的世界联系,割断了数学与现实生活的关联,单纯从概念到概念,从公式到公式,数学就成了无源之水、无本之木,数学的教学就必然枯燥乏味、失去活力,所传授的知识就不可能是全面深入的,更不可能给学生以数学的思想方法与精神实质的启迪,就不可能真正实现数学教学方面的要求.”李院士强调指出:“如果觉得数学纸上谈兵、毫无用处,觉得数学高不可攀、难于理解,觉得数学枯燥无味,甚至面目可憎,对其敬而远之、退避三舍,这样的数学教与学,无疑是失败了.”这是对数学教育教学目标的精辟阐述,笔者对此感同身受.
受众广、课时长的《高等数学》是大学数学类主干课程.在课程教学中积极渗透、有机融合数学建模的思想方法,积极引导、帮助在校大学生理解数学精神实质,掌握数学思想方法,增强运用数学的意识,提高数学能力,对培养学生的数学素养,全面提升教育教学质量有着积极的实际意义.虽然《高等数学》课程内容多、课时紧,应用问题数量、难度都很有限,但教学实践表明,教师立足课本内容,在深刻理解、充分利用、正确把握的基础上,抓住课堂教学契机,营造探究情境,引导学生积极自然顺畅地分析思考,使学生参与问题转化和解决的全过程,帮助学生领悟数学建模思想,掌握分析解决问题的方法,体会数学与现实世界的紧密联系及强大生命力,从而实现数学教育教学目标.
西安交通大学知名教授马知恩、王绵森主编的《高等数学简明教程》中的应用问题如减肥问题、疾病传播问题等,有典型性、有时代感,为教师用好、用活教材提供了很好的素材和发挥发展空间.笔者就为实现数学教学目标,在《高等数学》应用问题教学中,如何通过还原应用问题的真实与生动,展现数学与现实生活的关联及活力,把握数学建模的关键环节,提高“有效应用数学”的意识;如何通过引导学生积极、自然、顺畅地分析思考,化解对实际问题原型进行数学抽象的难点,提高“有效应用数学”能力这两方面所做的一些教学尝试小结如下,以求与同仁交流提高.
1 创设情境,共同探究
探照灯的聚光镜镜面是一张旋转曲面,它的形状由xOy坐标面上的一条曲线L绕x轴旋转而成.按聚光镜性能要求,在其旋转轴(x轴)上一点O处发出的一切光线,经它反射后都与旋转轴平行,求曲线L的方程.见图7—4(同济《高等数学》上册(第六版)306页,例2)
可以看到,教材为行文简明,在叙述应用问题时,已加入许多“数学化”了的东西,实际问题表述成了经加工过的“半成品”.如果教师照本宣科,少铺垫不引入,先入为主,解完了之,不仅错失了教育教学良机,学生遇到实际问题时,也可能不会分析、不知所措.笔者认为,应还原和再现应用问题的真实和生动,创设问题探究的情境,让学生体验“数学建模”创造性的过程,学会怎样“用数学”.笔者的讲法是:
问题提出:设计一款手电筒的反光镜面的形状.(问题一出,同学们跃跃欲试)
分析讨论:
1.从适宜批量生产、降低成本、保障利润考虑,设计的手电筒只有一个点光源,而且镜面规整光滑.故假设,镜面是由一平面曲线C绕该平面的一条直线L旋转而成.②由光学知识可知,要想手电筒射程远,射点亮,点光源经镜面反射后,应成为平行光束.③由对称性可知,点光源应当在旋转轴L上,且C应与L相交.于是,只要求出平面曲线C即可.

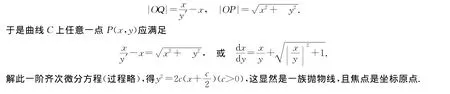
3.解释实际意义:由曲线C的方程可知,使反射光束成平行光束的旋转镜面,只能由抛物线绕其对称轴旋转而成,而且点光源在抛物线的焦点上.
2 突出重点,因势利导
设有一均匀、柔软绳索,两端固定,绳索仅受重力作用而下垂,试问该绳索在平衡状态时是怎样的曲线?见图7—6(同济《高等数学》上册(第六版)319页,例4)
课本解法:设绳索最低点为A,取y轴通过点A垂直向上,并取x轴水平向右,且|OA|等于某个定值(这个定值将在以后说明)(后略)
学生难免出现这样的疑惑:为什么要这样建立坐标系?为什么坐标原点不取在那个特殊点(即最低点)处?|OA|又是一个怎样的定值?求解比较知道,这样建立坐标系得出的曲线方程比较简洁整齐.但如果一开始就把这种后来总结出的相对完美的“高观点”强加给学生,必定会干扰学生自然顺畅地思考,使学生分析问题、解决问题时不得要领;而且学生失去了尝试的机会、认识链条人为地脱节,这不能不说是个不小的损失.
笔者尝试这样的展开:
问题提出:崇山峻岭间架设输电线路.两根电线杆间的电线通常呈下垂状.问在平衡状态下,电线是怎样的曲线.(课堂热议,不少同学猜测曲线是抛物线)
分析讨论:
1.由实际问题知,两电线杆距离足够大,故可假设电线是纤细且均匀的,设其线密度为ρ;(教材上图7-6曲线两端点不等高也可以顺理成章地解释了).为简化起见,假设电线是柔软的,仅受重力作用而下垂.
于是,只要求出平面曲线方程即可.

3 开放问题,深入研究
减肥问题.减肥就是减少体重,而体重变化取决于热量的吸收和消耗.设某人每天的饮食可产生A(J)的热量,用于基本新陈代谢所消耗的热量为B(J),用于锻炼所消耗的热量为C(J/kg).为简单计,假设增加或减少体重所需的热量全由脂肪提供,脂肪的含热量为D(J/kg).求此人开始减肥后体重随时间的变化规律.(马知恩、王绵森主编的《高等数学简明教程》上册282页,例2.11)
为了展示根据对实际问题的理解、研究的目的以及数学背景,对实际问题进行归纳、提炼、抽象、简化,做出必要、合理、恰当的假设,以提出数学内涵,建立数学模型的分析过程;展现将分析模型所得到的数学结论回到实际中去解释问题,以检验所得数学模型是否符合实际,以及如何修正假设,进一步研究问题的讨论过程,使学生深刻体会、理解和把握数学建模的关键环节,笔者与学生进行了以下的分析探讨.
问题提出:夏天快到了,你的朋友希望减肥,你能不能给他一些可以信服的说明和建议(话音未落,课堂气氛异常活跃).
讨论分析:
1.什么是减肥?科学地讲应当是减少多余的脂肪.但“多余的脂肪”这一指标不易检测和定量.为简化问题,假设体重的变化就是脂肪的变化(实际生活中人们也是乐于接受的).
2.知识表明,脂肪的变化取决于热量的吸收和消耗.考虑到实际操作即减肥计划的可行性,假设某人吸收的热量为一项:饮食A.消耗的热量为两项:①新陈代谢B;②运动锻炼C.易知A≥B.
3.人为能控制的因素是A,C,而C是减肥计划中重点操控的指标,故单位取为A(J/天),B(J/天),C(J/kg天).
4.为制定减肥方案,需求出开始减肥后,在因素A,B,C作用下,体重随时间变化规律.
设此人开始减肥时刻t=0时,体重为w0,时刻t时,体重为w(t).观察微小时段[t,t+d t]内此人热量Q的变化d Q.一方面:在[t,t+d t]内体重的改变量为d w,根据假设此即为脂肪的改变量.为转换成热量,设脂肪的含热量为D(J/kg),则d Q=D d w.另一方面,考虑在[t,t+d t]内该人在因素A、B、C作用下,热量变化情况.由于运动消耗C与体重有关,尽管[t,t+d t]内体重是不断变化的,但由于d t很小,体重变化很小,可以认为不变.故

② 短期达到“理想”体重如何做?

理论上可通过取定B,D(选择同年龄段的平均值),选取饮食A、运动锻炼C的最佳组合付诸行动,实现目标.
6.引申讨论,深入探究.
① 若假设不同,例如热量变化因素还是A,B,C,但单位取为A(J/天),B(J/kg天)C(J/天),结果如何?我们发现这样所得的方程及方程的解也不同.对结果进行分析,解释实际意义发现,虽然也能反映实际情况,但可得出的结论策略少了,达不到预期目的,需重新审视假设.通过比较发现,前面讨论分析的假设是较完美的.
② 对减肥问题,还能提出怎样的假设,进行怎样的讨论,以得出更好的减肥策略.
(这些问题可留给学生课后进行研究)
数学学习不仅仅是学习数学的概念、公式、定理和结论,懂得各种各样数学方法与手段,还在于领会和掌握数学的思想方法和精神实质,举一反三,灵活演绎,“学活”数学,更在于有明确的意识、相当的能力、有效地运用数学解决现实世界中种种实际问题,在于造就并形成一种优良的数学素养,从而对今后一生的发展都起到重要的积极的作用.数学教学、教法研究都应紧紧围绕这一目标展开.将数学建模思想方法运用于数学课堂教学,就是实现上述目标的有效途径之一.实践表明,先进的教育理念,明确的教学目标,扎实的科研、教学基本功,加之不断学习、钻研、思考,是做好教学工作的重要保证.大学数学的多门类课程及丰富的课堂教学内容,为数学教师实现教育教学目标提供了广阔的思考、发展、应用空间,有待于教师付出辛勤和努力,切实投入,认真实施.
[1] 李大潜.漫谈大学数学教学的目标与方法[C]//大学数学课程组委会[M]//2008大学数学课程报告论坛论文集.北京:高等教育出版社,2008:3-8.
[2] 刘来福,等.数学模型与数学建模[M].北京:北京师范大学出版社,1997.
[3] 同济大学数学系.高等数学[M].北京:高等教育出版社,2007.
[4] 马知恩,王绵森.高等数学简明教程[M].北京:高等教育出版社,2009.
G642.2
C
1672-1454(2010)增刊1-0136-05
