二维不对称两组分费米气体的拓扑相变

刘旭东,曾志生,梁军军

二维不对称两组分费米气体的拓扑相变

刘旭东＊,曾志生,梁军军

(山西大学理论物理研究所,山西太原030006)

研究了二维不对称两组分费米气体在零温时的相和相变,划分出不同极化率下正常相和Sarma相的区域.通过能隙和化学势在BCS-BEC渡越过程中的不连续性证明了量子拓扑相变的存在,并着重讨论了不同的配对质量对相变的影响,最后给出了相应的相图.

拓扑量子相变;BCS-BEC渡越区;Sarma相;鞍点自洽方程组

近年来,由于实验上的易操作性使得人们对超冷原子气体的研究产生越来越多的兴趣.对激光冷却、俘获中性原子等技术的研究已经表明,目前可以做到对势阱的几何形状,稀化气体的密度,温度以及两组分的费米气体间相互作用大小的控制[1-5],并观测到许多我们感兴趣的量子现象,例如Sarma超流相[6]、相分离和量子拓扑相变[7]等.在经典的超导BCS理论中,同一费米面附近具有相反自旋态的费米子可以配对,但在极化费米子体系中,由于自旋向上和自旋向下的费米子数目不相同,会形成两个不同的费米面.正是因为这两个不同费米面的存在,Sarma超流才可能会发生.在Sarma超流相中,弱耦合相互作用下的非稳定库伯对将不再存在.在实验上,对拥有不同数目的两个超精细态的费米子体系的研究已经取得了突破性的进展,且可以实现准二维气体,即在某一方向上限制费米原子的运动.在理论上,人们已经对三维不对称费米气体做了大量的工作.但对于二维费米气体来说,它有一些不同于三维情况的特性,如在二维情况下对于任意的耦合都存在束缚态,而对三维时只存在一个临界的耦合强度来形成s波束缚态.本文主要基于泛函积分理论,用数值方法来研究二维配对质量不同的两组分费米气体在零温时的拓扑相变.

1 理论模型

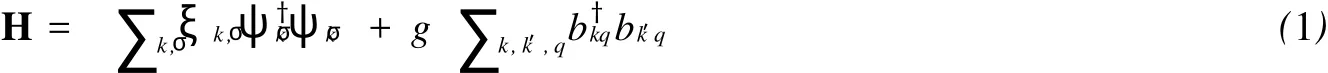
对于一个两组分稀化费米气体的系统,其哈密顿量(ħ=1)为这里赝自旋σ=↓,↑表示超精细态,ψkσ是费米场湮灭算符,bkq=ψ-k+q/2↑ψk+q/2↓,ξk,σ=εk,σ-μσ其中εk,σ=k2/ (2mσ)是动能,μσ是费米子的化学势.这里不同质量和分布的费米子可由相应的化学势μσ控制.g表示原子间相互作用耦合系数.下面我们概述基本理论.

1.1 高斯有效作用量

配分函数可由虚时泛函积分给出:Z=∫DΦDΦ＊exp(-S[Φ,Φ＊]),这里配分函数Z中的作用量S=.取辅助场为平均场近似下的能隙,作Hubbard-Stratonovitch变换,得到Z=∫exp(S0)DΔ†DΔ.在平均场近似下鞍点作用量S0:

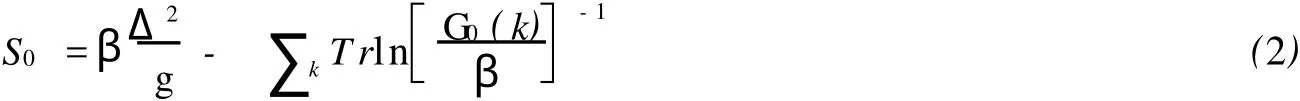
这里β=1/T,k=(k,ωn)其中费米Matsubara频率ωn=(2n+1)π/β,Δ是序参量,G0-1(k)是费米传播子的逆矩阵.矩阵G0-1(k)定义为:

热力学势鞍点贡献为Ω0=S0[Δ]/β,它可以写为:

这里f(x)=[exp(βx)+1]-1是费米分布,Ek,±=(ξ2k,++Δ2)1/2±ξk,-是准粒子和准空穴的能量,其中ξk,±= (ξk,↑±ξk,↓)/2=k2/(2m±)-μ±,约化质量定义为m±=2m↑m↓/(m↓±m↑),化学势重新定义为μ±=(μ↑±μ↓)/2.

1.2 耦合方程

自旋为σ的粒子数可用Nσ=-∂Ω/∂μσ表示.由于涨落对粒子数的贡献会在温度趋于0的极限下消失,这样只需考虑来自鞍点近似的贡献.粒子数方程可写作,

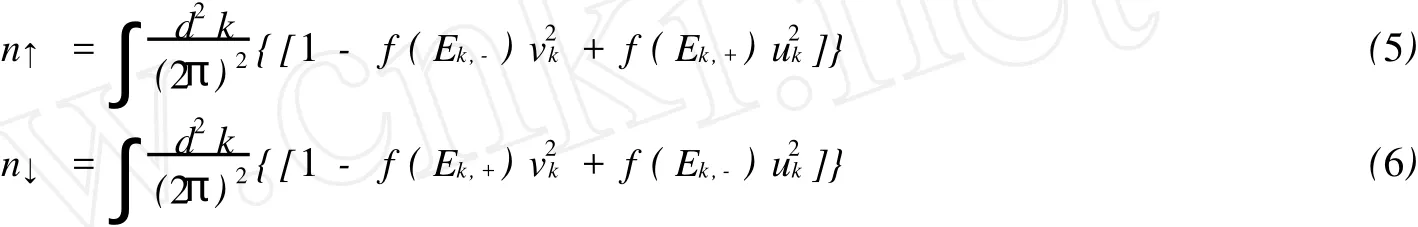
这里nσ=N0,σ/V是粒子数密度,uk2=(1+ξk,+/Ek)/2,vk2=(1-ξk,+/Ek)/2,其中Ek=(Ek,++Ek,-)/2.能隙方程可由δS0/δ Δ=0得到,

在二维情况下,束缚态能量比相互作用耦合系数g更适合描述BCS-BEC渡越.束缚态方程可写作,

将束缚态方程(8)与能隙方程(7)联立消去因子g后,可与粒子数方程组成鞍点自洽方程组.对于上面介绍的所有的方程都取零温极限:θ(-Ek,±)=limβ→∞f(Ek,±),这里θ(x)是阶跃函数.下面利用数值方法求解鞍点自洽的方程组.

2 数值计算

在零温极限下,鞍点自洽方程组能够恰当地描述从BCS-BEC极限的超流演化过程.将质量比mr=m↑/ m↓,极化率P=(n↑-n↓)/(n↑+n↓),束缚态能量ε0作为参数,利用数值方法求解序参量Δ和化学势μ+= (μ↑+μ↓)/2.首先对方程作无量纲化处理,取费米能量εF为基本单位.更直观地,取kB=ħ=1.这里我们只考虑6Li和40K的混合费米气体,取mr=0.15.

2.1 拓扑量子相变标志

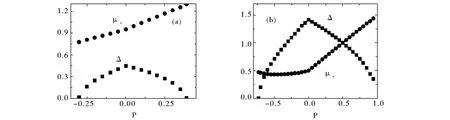
图1 μ+和Δ在不同ε0/εF下随极化率P的变化曲线,其中图(a)中ε0/εF=0.1,图(b)中ε0/εF=1.0Fig.1 Plots ofΔ,μ+(units ofεF)as a function of P,(a)whenε0/εF=0.1,(b)whenε0/εF=1.0

量子相变是指在绝对零温下由于量子涨落引起的相变现象,其系统的对称性发生了自发破缺,而拓扑量子相变中系统不存在对称性自发破缺.在极化的费米体系中由于配对的不平衡,出现新的量子相,即Sarma相或Breached Pair(BP)相.拓扑量子相变标志表现为序参量Δ和化学势μ+在拓扑相变点处有个拐点.在图1中可以清楚地看出在质量比mr=0.15和束缚能量不同时序参量Δ和化学势μ+的变化关系,从图1(a)中可以看出当P趋于0时序参量Δ和化学势μ+的变化是非解析的,这标志着量子相变从BP2(Breached Pair II)相(P<0)到BCS超流相(SF)再到BP2相(P>0).同样地情况出现在图1(b)中,这里的相变标志也在P→0,只是这时的量子相变从BP1(Breached Pair I)相(P<0)到BCS超流相(SF)再到B P1相(P>0).注意到图1中在P的两侧是非对称的,这与在质量比为mr=1的对称情况[8]成鲜明地对比.

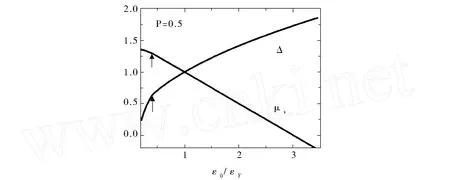
图2 μ+和Δ在P=0.5时随束缚能ε0/εF的变化曲线,其中箭头指示拐点Fig.2 Plots ofΔ,μ+as a function ofε0/εFwhenP=0.5.The arrows indicate the cusp point

在图2中取P=0.5,这时所有自旋向下的费米子与相同数目自旋向上的费米子配对形成N↓个玻色子,而剩余自旋向上的费米子则处于未配对状态.从图2中我们可以看到在束缚能ε0/εF=0.41从BCS极限到BEC极限的连续变化中存在一个拐点,这标志着量子相变从BP2相到BP1相.这里拐点的位置可以从能隙Δ和化学势μ+在拐点两端的不同行为来判断.

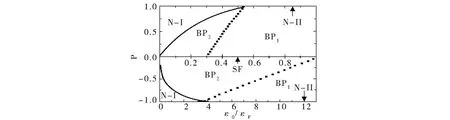
图3 在ε0-P平面的相图Fig.3 Phase diagrams in the planeε0-P

2.2 拓扑相图

拓扑相图表示了在动量空间中量子相在没有对称性破缺的情况下的改变情况.它描述了零温时系统的基态.换句话说拓扑相图是对量子相的一种分类[9].根据两个准粒子激发态能量Ek,±的零点数决定量子相,可以将量子相分成三类:Breached pair I相(BP1),Breached pair II相(BP2)和BCS超流相(SF).BP1相:一个有效的费米面(图3中BP1表示的区域).事实上准粒子激发能这时有两个零点,但是其中一个零点的k值是负值,这在物理上是没有意义的.BP2相:两个有效的费米面(图3中BP2表示的区域).准能量有两个零点,且每个零点的k值都是正值.SF相:没有有效的费米面(图3中SF表示的区域),在这种情况下激发态能量没有零点或者是两个零点的k值是负值.对于第一种情况,激发态是有能隙的,这就是经典的BCS超流相.对于第二种情况,化学势μ+必须是负值,极化率P为0.

从图3中清楚地看到部分极化正常相(N-I)和Sarma超流相的边界在P=0的两端是不对称的,这与质量相等的情况[7]成强烈地对比.由BP1和BP2的边界可看出随着P的增加ε0/εF的值增大,在P>0时BP1相和BP2相的边界对应的束缚能量较小,而在P<0时BP1相和BP2相的边界对应的束缚能量较大. BP1相到SF相和BP2相到SF相的临界线是P=0.而完全极化正常相(N-II)跟BP1相的边界在P=±1处.

3 结论

通过以上分析我们发现零温下二维费米气体在配对质量不同时存在拓扑量子相变,临界线与配对粒子之间的质量比mr有关.本文只讨论了6Li和40K组成的混合费米气体,对于其他的不同质量的冷原子配对,结论是类似的.需要指出的是,这里只讨论了零温的情况,而在有限温度情况下,由于热涨落的存在,拓扑相变特征即曲线的不光滑点(cusp)不是很明显,但可以通过计算热容量、压缩率等特性来研究.同时,文章只限于讨论严格意义的二维系统.在今后的工作中,我们将研究准二维费米气体的低温拓扑量子性质.

[1] TRUSCOTT A G,et al,Observation of Fermi Pressure in a Gas of Trapped Atoms[J].Science,2001,291:2570-2572.

[2] MARTIN W,et al.Fermionic Superfluidity with Imbalanced Spin Populations[J].Science,2006,311:492-496.

[3] GUTHRIE B.PARTRIDGE,et al.Pairing and Phase Separation in a Polarized Fermi Gas[J].Science,2006,311:503-505.

[4] REGAL C A,J IN D S.Measurement of Positive and Negative Scattering Lengths in a Fermi Gas of Atoms[J].Phys Rev Lett,2003,90:230404-230408.

[5] WILL E E,SPEIGEL HALDER F M,et al.Exploring an Ultracold Fermi-Fermi Mixture:Interspecies Feshbach Resonances and Scattering Properties of6Li and40K[J].ibid,2008,100:053201-053205.

[6] SARMA G.On the Influence of a Uniform Exchange Field Acting on the Spins of the Conduction Electrons in a Superconductor[J].Phys Chem Solids,1963,24:1029-1032.

[7] ISKIN M,SÁDE MELO C A R.Two-species Fermion Mixtures with Population Imbalance[J].Phys Rev Lett,2006,97: 100404-100408.

[8] DU Jia-jia,LIANGJun-Jun,CHEN Cheng.Asymmetric Two-component Fermi Gas in Two Dimensions[J].Phys Rev A, 2009,80:023601-023610.

[9] GUBANKOVA E,SCHMITT A,WILCZEK F.Stability Conditions and Fermi Surface Topologies in a Superconductor [J].Phys Rev B,2006,74:064505-064521.

Phase Diagram of Asymmetric Two-component Fermi G as in Two Dimensions

LIU Xu-dong,ZEN G Zhi-sheng,LIANGJun-jun
(Institute ofTheoretical Physics,Shanxi University,Taiyuan030006,China)

We investigate the superfluid phase and phase transition in two dimensions at zero temperature for asymmetric Fermi gas and the regions corresponding to normal and Sarma phase for different polarization are identified.The existence of quantum topological phase transition by is proved by varying energy gap and chemical potential in BCS-BEC crossover.The effect of quantum phase transition with different mass ratio is discussed and the topological phase diagram in this region is given.

topological phase transition;BCS-BEC crossover;Sarma phase;saddle-point self-consistent equations

O413

A

0253-2395(2010)03-0393-04

2009-12-15;

2010-03-25

刘旭东(1984-),男,山西太原人,在读硕士,研究方向:玻色-爱因斯坦凝聚.E-mail:liuxd1984@gmail.com