指数稳定双系统同时近似可观测的充分条件

2010-11-02李胜家

山西大学学报（自然科学版） 2010年3期

关键词：双系统生成元充分条件

杨威,李胜家

指数稳定双系统同时近似可观测的充分条件

杨威,李胜家

(山西大学数学科学学院,山西太原030006)

利用指数稳定半群生成元的谱理论,得到了判断指数稳定双系统在[0,∞)同时近似可观测的充分条件.

线性系统;指数稳定;同时近似可观测性

0 引言

线性系统的控制理论在航天航空、航海、工业生产过程以及社会经济等领域有着非常广泛的应用.学者们一直对弹性振动系统的建模和振动控制问题有着广泛而深入的研究,在振动系统的谱分析、能控性、反馈镇定和边界控制等方面取得了很多成果[1-4].此外,许多学者开始寻找多系统同时可控和同时可观测的判断条件,即:对于同一输入、输出如何确定它们是同时可控和同时可观测的,见文献[5-7].但是,绝大部分研究成果都集中于具体双系统方程的同时可控性和可观测性,对于抽象的双系统方程结果很少.本文考虑如下两个抽象指数稳定双线性系统(A1,C1)和(A2,C2)的同时近似可观测性,其状态分别用z1和z2表示:

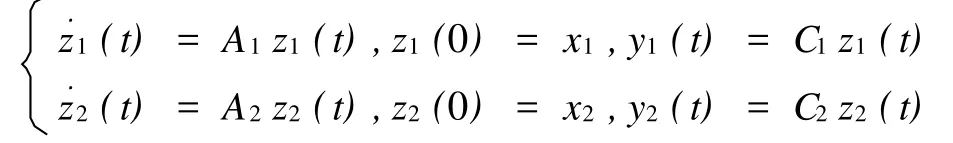
其中,“·”表示对时间t的微分,A1和A2分别是相应状态空间上强连续算子半群的生成元,C1和C2为相容性观测算子.我们利用指数稳定半群生成元的谱理论,得到了判断指数稳定双系统在[0,∞)同时近似可观测的充分条件.

1 主要结果及其证明

假设X,Y是Hilbert空间,算子A是空间X上强连续半群(T(t))t≥0的无穷小生成元.定义Hilbert空间X1=(D(A),‖·‖1),其中‖z‖1=‖(βI-A)z‖,β∈ρ(A)固定,且算子C∈L(X1,Y)是相应于半群(T(t))t≥0的相容性观测算子.容易验证,若算子C∈L(D(A),Y),则算子C一定是相容性观测算子.算子Ψ∞:D(A)⊆X→L2([0,∞),Y)定义如下:

显然算子Ψ∞可以连续的延拓到X上,称Ψ∞为由算子A和C所成的输出映射.我们称系统:

在[0,∞)上是近似可观测的,如果对于任意的非零元x∈D(A)都有:∫∞0‖CTtx‖2dt>0成立.

引理1[8]如果系统:

在[0,∞)上是精确可观测的,那么下面的估计式成立:

存在常数m>0,使得对于任意的s∈C-(其中C-表示复平面C的左开半平面)和任意的x∈D(A),都有:

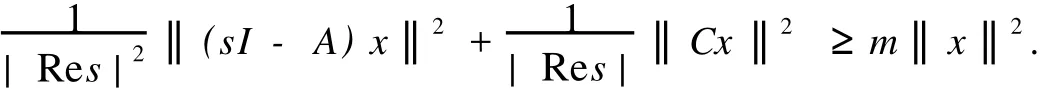
事实上,可以取上式中的m为由系统本身所确定的常数:

引理2 设A1在Hilbert空间X1上生成C0-半群(T1(t))t≥0,A2在Hilbert空间X2上生成C0-半群(T2(t))t≥0.那么,算子在X1×X2上生成指数稳定C0-半群的充要条件为C0-半群(T1(t))t≥0和C0-半群(T2(t))t≥0均为指数稳定的.

证明 (必要性)由于(T1(t))t≥0和(T2(t))t≥0都是指数稳定的,因此对于任意的x1∈X1和x2∈X2都存在γx1<∞和γx2<∞使得:

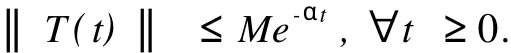
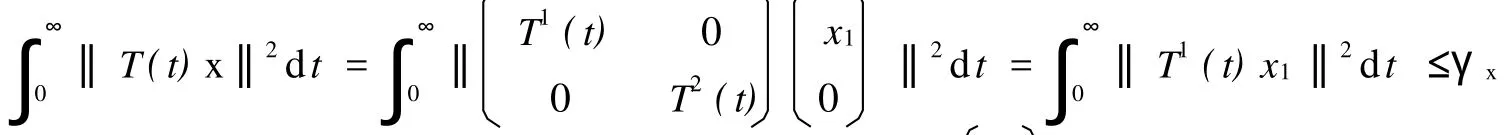
由x的任意性知,C0-半群(T1(t))t≥0为指数稳定的.同理,取可得,C0-半群(T2(t))t≥0为指数稳定的.

引理3[8]设A是Hilbert空间X上强连续半群的生成元,如果‖(sI-A)-1‖在ρ(A)上是有界的,那么X={0}.

设系统(A1,C1)和(A2,C2)在[0,∞)上均是精确可观测的,则利用引理1可以计算出相应的m1和m2.当他们满足一定条件时,便得下述定理.

定理1 设A1在Hilbert空间X1上生成指数稳定C0-半群(T1(t))t≥0,A2在Hilbert空间X2上生成指数稳定C0-半群(T2(t))t≥0.设Ci∈L(D(Ai),Y)是相对于(Ti(t))t≥0,(i=1,2)的相容性观测算子且系统(A1,C1)和(A2,C2)在[0,∞)上均是精确可观测的.假若系统:

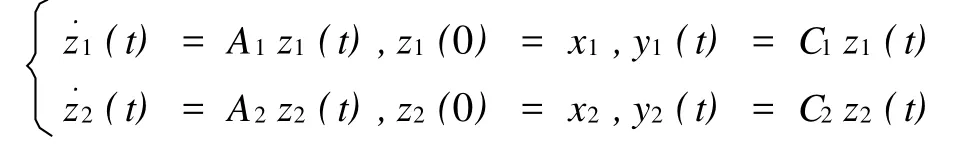
满足:

那么系统(A1,C1)和(A2,C2)在[0,∞)上是同时近似可观测的,其中α=min(ω1,ω2),-ω1,-ω2分别为半群(T1(t))t≥0和(T2(t))t≥0的增长阶.

利用半群的性质可知,对∀x∈D(A)且∀t,τ≥0,有

再利用半群的指数稳定性知:

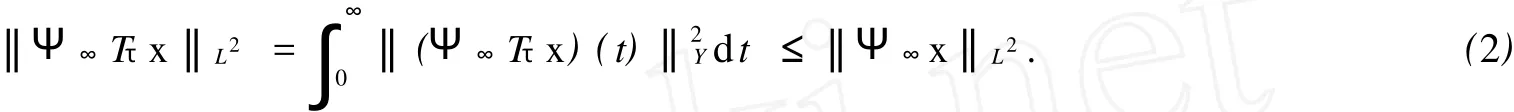
因为D(A)在X1×X2中稠密,且(2)式两端都是关于x的连续函数,故上式对于任意的x∈X1×X2和τ≥0均成立.

令Z=KerΨ∞,因此Z是X1×X2的一个闭子空间,且Z是T的一个不变子空间.令¯T为T限制在Z上的作用,即:¯T=T|Z.因此¯T是Z上的强连续半群,且设¯A是¯T的生成元,满足:

D(¯A)=D(A)∩Z,D(¯A)⊂KerC,

即:¯A为A限制在D(¯A)上的作用.

由引理1以及系统(Ai,Ci)(i=1,2)在[0,∞)上的精确可观测性,任给s∈C-和x∈D(¯A)可知: C也是相容的.定义算子Ψ∞:D(A)→L2([0,∞),Y)为

此时取s∈C-α/2,我们有:

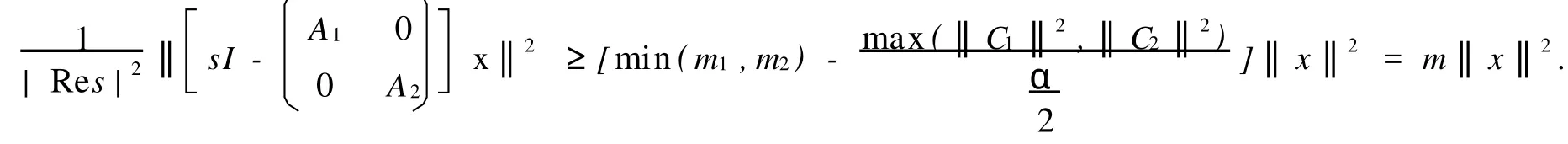
故对于任意的s∈ρ(¯A)∩C-α/2

由引理2可知¯T是指数稳定的,故‖(sI-¯A)-1‖是有定义的且在半平面{s∈C|Res>-α/2}是有界的.利用(3)可知‖(sI-¯A)-1‖在ρ(¯A)上是有界的.由引理3知:Z={0},因此对于任意的x≠0,有Ψ∞x≠0.故系统:

在[0,∞)上是近似可观测的.

[1] LIONS J L.Exact Controllability,Stabilization and Perturbations for Distributed Systems[J].S IA M Review,1988,30:1-68.

[2] CHAI Shu-gen,LIU Kang-sheng.Observability Inqualities for the Transmission of Shallow Shells[J].S ystems Control Letters,2006,55:726-735.

[3] CERPA EDUARDO.Exact Controllability of a Nonlinear Kortewegde vries Equation on a Critical Spatial Domain[J].S IA M J Control Optim,2007,46:877-899.

[4] DEHMAN B,LEBEAU G.Analysis of the HUM Control Operator and Exact Controllability for Semilinear Waves in U-niform Time[J].S IA M J Control Optim,2009,48:521-550.

[5] TUCSNAK M,WEISS G.Simultaneous Exact Controllability and Some Applications[J].S IA M J Control Optim,2000, 38:1408-1427.

[6] AVDONIN S A,WILLIAM.Simultaneous Control Problems for Systems of Elastic Strings and Beams[J].S ystems Control Letters,2001,44:147-155.

[7] KAPITONOV B,MENZALA G.Simultaneous Exact Controllability for Maxwell Equations and for a Second-order Hyperbolic System[J].Electronic J Dif f erential Equations,2010,24:1-13.

[8] RUSSEL D L,GEORGE W.A General Necessary Condition for Exact Observability[J].S IA M J Control Optim,1994, 32:1-23.

Sufficient Conditions for Simultaneous Approximate Observability of Two Exponentially Stable Systems

YANG Wei,LI Sheng-jia
(School of Mathematical Sciences,Shanxi University,Taiyuan030006,China)

By using the spectral theory of the generator of exponentially stable semigroup,the sufficient conditions for simultaneous approximate observability in[0,∞)of the following two exponentially stable systems are obtained.

linear system;exponentially stable;simultaneous exact observability