基于模糊神经网络控制的供热系统

2010-10-26刘维生

唐山师范学院学报 2010年2期

刘维生

（唐山师范学院物理系，河北唐山 063000）

目前中国北方城镇共有供暖建筑65亿m2，其中约70%采用不同类型的集中供暖[1]，因此供热节能是建筑节能工作中潜力最大、最主要的途径，应该作为当前开展建筑节能工作的重中之重。

许多原有小区在进行供暖设计时都是基于原有铸铁散热器以及房屋的散热公式进行推算，并根据居民的反馈进行粗放式的供热控制，不但不能均衡地控制小区内房屋的温度并且会造成很大的浪费。随着供热管线的老化以及居民装修时对散热设备的更新，原有的模式已经远远不能达到目前供热的要求。

如果完全仿照新式小区采用每户独立进行控制的方式需要对供热系统进行较大的改造，资金投入较大，文章建立了一种基于神经网络多点温度预测的供暖控制系统，通过该系统对小区集中式供暖进行最优控制，能够达到通过统一调节对小区内的房屋进行均衡供热，并最大限度的减小能源的消耗的要求，而且不需要对小区原有的供暖设施进行大规模改造，需要的资金较小。

1 数学模型（Teaching model）

供暖区域内住户的室内温度，受室内供热设备在整体供暖系统中的位置、室内散热器的散热性能、房屋的环境、供热系统整体结构、供热的入口温度、供热入口流量、供热回水温度、环境温度等因素的影响。一般来说，当房屋建筑施工完毕后，室内供热设备在整体供暖系统中的位置、房屋的环境和供热系统整体结构就不会再发生改变，室内的散热器一般在较长的一段时间内也不会发生变化，因此室内温度主要由供热的入口温度、供热入口流量、环境温度决定，即

其中 tr是供热系统的入口水温，pr是供热系统的入口水流量，te是外界环境温度，th是供热系统的回水温度。

其中供热系统的入口水流量pr是由水泵的转速决定的，tr是由锅炉供水流量和供热锅炉的加热效率决定的。

其中，ρ是指供热水泵电机的转速，Sg是指供水管道面积。

其中 Vr是指锅炉燃料供应速度；β是指燃料的平均加热效率；Δt是指供热媒介（一般是水）被加热的时间。

系统能耗

其中 0＜Vr＜=Vmax。

在系统实际运行控制过程中，调控目标就是通过调节燃料供应速度 Vr以及供暖时间来调节受供用户的室内温度，在满足供暖温度要求的基础上使得系统能耗最低。

系统温度控制要求是采暖用户的室内最低温度

Tmin是政府规定的供暖最低温度，目前是16℃。

2 系统控制（System Control）

为了更加及时有效地对供暖区域内的供暖温度进行调节，在保证受供用户利益的前提下，最大限度地降低系统能耗，需要及时地获得各个受供用户的供暖温度。因此，在供暖区域内均匀地设置了n个温度监控点，根据这些检测点的温度变化对系统进行控制。由于供暖系统具有大延迟的特性，需要根据对这些检测点的温度预测确定调节的幅度，因此系统包括监测点温度预测建模和系统控制两部分。

2.1 监测点温度预测建模

2.1.1 基本模型

室内温度主要由供热的入口温度、供热入口流量、供热回水温度、环境温度决定，同时还受室内供热设备在整体供暖系统中的位置、室内散热器的散热性能、房屋的环境、供热系统整体结构等因素的影响，因此很难精确地定义出函数fi来计算被供暖用户的供暖温度。由于神经网络能以任意精度近似任何连续的非线性函数，并且经过学习训练后的神经网络能够利用其并行计算能力显著地提高系统的性能，因此本系统采用经典的前向3层神经网络对fi模拟，并根据监测点的历史供暖数据进行网络训练。

在影响检测点温度的几个因素中，室内供热设备在整体供暖系统中的位置、室内散热器的散热性能、房屋的环境、供热系统整体结构一般不会发生变化，因此在输入层中设置5个神经元，分别为供热系统入口温度、供热系统入口流量、环境温度、供热回水温度、预测点当前温度。输出层只有一个神经元，输出结果为预测的温度；隐含层设置10个神经元。相邻层之间的节点采用全连接的方式，同层之间的节点无连接，不相邻层之间没有直接连接。神经网络连接图1所示。

神经元的激励函数采用普通的Sigmoid函数：

其中常数c可以任意选定，其倒数1/c称为温度参数[4]，在本系统中将c设置为2。

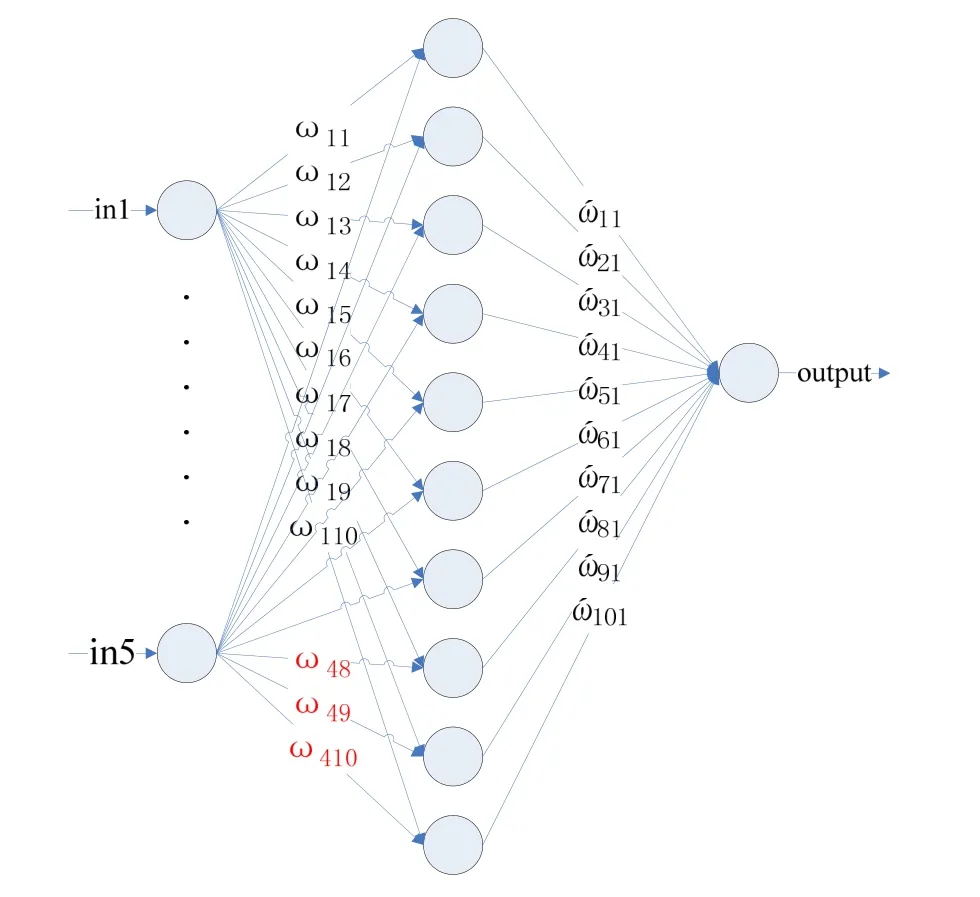
图1 供热温度预测神经网络简图

2.1.2 输出神经元模糊化修正

由于神经网络的输出要求是预测检测点的温度，而且本系统用于供暖系统的温度控制，温度不需要绝对精确，因此对于输出神经元的输出进行如下修正：d = [0 ×Tmax]，其中Tmax是指系统设定的最高供暖温度，根据平均的散热器效果计算，本系统设置Tmax=32℃。

2.1.3 网络训练算法

传统的误差逆向传播算法采用梯度下降的方法，在权矢量空间中求取误差函数的极小值[3]，使得训练权值能够快速收敛，但是容易陷入局部极值点。遗传算法（Genetic Algorithm，GA）是一种模拟自然界生物进化过程与机制的全局优化搜索算法，具有不依赖问题模型特性、全局最优性、隐含并行性及解决非线性问题的鲁棒性强等优点[2]。文章采用了一种改进的GA算法，通过对适用度函数的选择压力进行自适应调整，并以误差反向传播算法对GA进化方向进行一定的指导，使得训练结果在全局范围内能够进行快速地收敛最优点。

本模型以图 1神经网络中所有神经元连接权值的集合作为遗传编码 Y={ω1，1，…，ω5，10，ώ1，1…，ώ10，1}，每个遗传编码中都包含60个权值因子，每个权值因子使用实值编码。

选择合理的使用度计算函数是使用遗传算法计算的关键，为了计算每个遗传因子的适应度，采用对给定的输入集和输出集计算出每个神经网络的全局误差作为适应度，即基本的适应度计算函数为：

其中Oi为输入第i个训练样本时的输出值，di为第i个样本的实际输出值，k为训练样本的大小。

为了避免在进化初期，选择压力过大，使搜索很快被约束到一个小的子搜索空间，搜索行为从求泛迅速转入求精阶段[5]，以及在进化后期，选择压力过小会使遗传算法迭代趋近于随机搜索过程[4]，本系统采用轮盘赌的方式进行遗传因子的选择，并对遗传因子的选择概率进行自适应调节，第 i个遗传因子的选择概率算法如下：

第i个遗传因子的调整后适应度

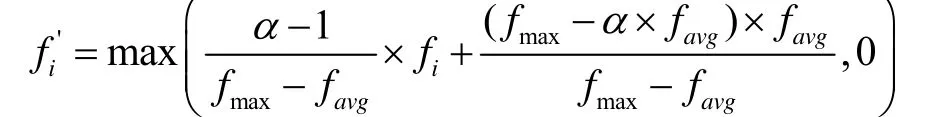
其中fmax是群组的最大适应度，favg是群组的平均适应度，

进行基因重组时，采用异常基因淘汰的原则，将误差最大的基因因子（连接权值）进行交叉重组。重组方法如下：

（1）对于进行基因重组的基因Yi和Yj，首先计算各自最大的误差Δmax；

（2）根据各自的Δmax进行误差反向传播计算；

对于被选择进行变异的基因Yi，选择该基因预测的最大误差根据误差反向传播公式计算出的第一层连接权中误差最大的连接权值ω和第二层连接权中误差最大的连接权值因子ω'分别进行基因变异处理。

变异计算公式为：

其中Δω是使用Δmax根据误差反向传播公式计算出的连接权ω的误差，Δmax是基因 Yi的最大误差，Δavg是基因 Yi的平均误差。

2.2 系统控制过程

本供暖控制系统的控制过程如下：

（1）使用以上的算法对神经网络预测模型进行训练。

（2）根据设备的控制精度，将“水泵转速”、“锅炉燃料供应速度”在可调节范围内进行离散化处理。

（3）实时监控监测点温度，控制是否进行温度调节：

为了避免系统过于灵敏受到意外扰动（比如某检测点进行开窗通风导致室内温度下降）而进行调整，在系统中设定了两个调整策略，进行鲁棒性控制。

①系统内部1/3的检测点温度发生同向变动（上升或者下降）；

②外部温度发生变更导致预测温度发生变化。

（4）如果需要进行供暖控制，根据当前的设备参数以及调节趋势（温度升高时向下调节，温度降低时向上调节），使用新的参数预测各点温度调节依次进行温度预测，找到满足温度控制要求的最小参数。

（5）向下调节

①使用当前控制参数-Δ作为预测调控参数；

②使用预测调控参数进行温度预测计算；

③判断预测温度是否满足要求，如果不满足要求，设置当前控制参数=预测调控参数，转入步骤①，如果满足要求，设置最优控制参数=当前控制参数，转入步骤（7）。

（6）向上调节

①使用当前控制参数+Δ作为预测调控参数；

②使用预测调控参数进行温度预测计算；

③判断预测温度是否满足要求，如果满足要求，设置最优控制参数=预测调控参数，转入步骤（7），如果不满足要求，设置当前控制参数=预测调控参数，转入步骤①。

（7）使用计算出的最优参数进行供暖设备调节。

3 仿真与应用（Simulation and Application）

某小区老旧供热面积大约 8Km2，1台美国瑞佰克模块直流式燃气热水锅炉（全铜），单台发热量为504.6KW（互为备用）采用燃气锅炉进行供热。以该小区 2004、2005、2006、2007年的供热情况作为基准进行神经网络训练，对2008年的供暖情况进行模拟并与实际数据进行进行对比。

原来采用人工控制的情况下，有两种控制模式，第一种在每年的11月15日～12月24日以及次年的2月5日～3月15日，此时气温变化不大，每天平均运行12小时，而第二种在12月25日～2月4日气温变化快，温度是每年平均的最低点，为热消耗最大的季节，每天平均运行16小时，而且采用人工只是控制供暖时间而不能调节锅炉的送气速度。图2、图3分别是使用本控制系统对2008年11月29和2009年1月10日分别进行供暖控制得到的系统调控数据与实际调节参数的对比结果，其中图形的横坐标是时间（将一天划分为24小时），纵坐标是供暖锅炉燃气输入速度。