高架桥地震响应的半主动控制研究

陈送财, 李锦华

(1.安徽水利水电职业技术学院市政工程系,安徽 合肥 231603;2.上海大学 土木工程系,上海 200072;3.华东交通大学 土木建筑学院,江西 南昌 330013)

为了控制工程结构的地震振动,过去常用的方法是在结构上安装高阻尼橡胶圈或粘滞阻尼器,利用这些装置增加结构的模态阻尼比,达到隔震的目的。在高架桥梁工程中,这种隔震技术得到了广泛的研究与应用。然而,隔震技术在实际工程应用中,存在一定的局限性[1]。近年来,国内外学者将用于汽车悬吊结构振动控制的磁流变(MR)阻尼器应用到土木工程结构地震振动控制上,并取得了较好的效果[2,3]。MR阻尼器是一种典型的半主动控制元件,它具有构造简单、响应速度快、耐久性能好、阻尼力大且连续可调等优点。特别突出的是MR阻尼器所需要的能源很低(小于50 W),其工作电压只需2～25 V;即使地震中能源中断,MR阻尼器仍可作为被动耗能装置(粘滞阻尼器)继续发挥控制作用(fail-safe),具有很强的鲁棒性。尽管如此,半主动控制技术在实际工程中的运用还很少,还处于试验及理论研究阶段,而且主要的研究对象是框架结构。文献[4,5]对公路桥梁的半主动控制做了试验与数值分析,但MR阻尼器在高架桥地震振动中作半主动控制设备的应用还很少,而且相应的理论及试验研究也非常有限;文献[6]将高架桥梁典型墩-支座-桥面结构简化为一个2自由度的线性系统,进行了MR半主动控制的研究,得到了比较明显的控制效果,但对整体高架桥多自由度结构体系的研究成果很少。因此,本文将采用MR阻尼器为作动器,考虑其动力特性,使用剪切型最优控制(clipped-optimal control)算法对高架桥的多自由度结构体系进行半主动控制研究。

1 高架桥的分析模型

由于地震地面运动是一种随机过程,运动极不规则,而高架桥结构为各种构件组成的空间体系,其动力特性十分复杂,故由地震引起的结构震动是一种复杂的空间震动。在进行分析时,常需要对其做出一些简化和假设。为了便于计算,需要把具体的结构体系,在满足工程计算精度要求的条件下,抽象为质点体系。对于这种由主梁、支座、桥墩组成的体系建立力学模型,简化的方法是把主梁视为刚体,而把桥墩的质量集中在墩顶,从而构成多自由度结构体系。假设主梁是连续的,而且桥墩受到同样场地的地震激励作用,当各桥墩的特性相同且支座具有同样的性能时,可以使用2自由度体系进行研究。否则,需要采用多自由度(MDOF)体系模型来研究体系的运动状态。对于连续梁桥,本文采用图1所示的模型分析。

图1 高架桥M DOF体系的分析模型

其中,Ms、Cs和Ks分别表示结构的质量、阻尼和刚度矩阵;x为结构相对地面的位移向量是一维地面加速度;F是阻尼设备提供的控制力向量;r为单位列向量;E为阻尼的位置矩阵。

系统的状态空间方程可表示为:

2 变阻尼器的模型

到目前为止,MR阻尼器的力学模型,大致可以分为参数化模型和非参数化模型2类。由于非参数化模型具有十分复杂的结构,因而国内外学者在充分考虑磁场磁流变流体屈服过程具有不同阶段的特点和MR阻尼器结构特点的基础上,对参数化模型的研究比较多,建立了一些MR阻尼器的参数化力学模型,如宾汉姆(Bingham)粘-塑性模型、修正的宾汉姆粘-塑性模型、Bouc-Wen模型、修正的Bouc-Wen模型、现象模型等。本文采用文献[7]在Bouc-Wen模型的基础上提出的修正的 Bouc-Wen模型。此模型的端部力控制方程为:

3 半主动控制实现

对于经典的线性二次型最优控制问题(即LQR控制)[8],选用如下的目标函数:

其中,Q和R为状态向量和控制力的权矩阵函数,要求为半正定矩阵和正定矩阵;tf为外激励的作用时间。在满足外激励为零均值的随机过程的前提下,优化(6)式目标函数,得到最优控制力:

其中,P为 Riccatti矩阵,满足如下的代数Riccatti方程:

(8)式一般可采用数值方法求解。对于确定的系统,合理选择Q、R矩阵是使系统得到有效控制的关键。为了考虑体系的总体控制效果,本文以系统能量最小为控制目标。设 Q和R分别为:

其中,α1、β1为待定系数;I为单位矩阵。

本文采用文献[3]提出的剪切型最优控制(clipped-optimal control)算法。首先设计一个线性的最优反馈增益矩阵L,依据当前的系统状态Z,算出最优控制力 Fopt,而这个力常常不能由MR阻尼器产生,为了使MR阻尼器产生的力F与最优控制力近似,可以调节输入电压来改变MR产生的力。具体调节方式为:如果F=Fopt,则维持当前的电压不变;如果F＜Fopt,并且2个力的方向相同,则增大电压到最大值,以产生更大的控制力;否则,将电压调整为零。

4 实例分析

以京福高速公路江西段的重点工程——桃木岭高架桥为例。该桥各墩高在15～86 m之间,为了简化计算,取其中4跨进行分析,动力分析模型如图1所示。

4.1 计算参数与控制器的设置

该桥基本参数如下:主梁箱梁质量 M1=4 486.3 t;各桥墩的质量分别为M2=252.39 t,M3=446.48 t,M4=437.92 t;桥墩的抗推刚度分别为K2=39 444 kN/m,K3=26 751 kN/m,K4=28 350 kN/m;高阻尼橡胶支座的阻尼系数C=3 120 kN ◦s/m,刚度为K=3 500 kN/m;伸缩缝的刚度为K1=K5=30 000 kN/m;结构阻尼矩阵为其质量矩阵和刚度矩阵的线性组合,组合系数由前2阶振型的频率与阻尼比确定,阻尼比为 ξ1=0.05,ξ2=0.07 。

MR阻尼器的各参数见表1所列[7],MR阻尼器的设置位置如图1所示,每个位置设置4个阻尼器。

4.2 控制效果判断

为了满足可靠性和经济性等要求,有效减小结构的振动反应是结构控制的目的。为了衡量振动控制的效果,引入减振率的概念,其值根据桥梁结构的水平、纵向位移反应的大小来确定,即

4.3 数值结果分析

以3种地震记录波为输入,分别是:EI-Centro地震波,加速度峰值为0.34g;Taft地震波,加速度峰值为0.10g;天津地震波,加速度峰值为0.15g。

表1 不同控制策略下高架桥的位移减振率 %

表1列出了高架桥在3种地震波激励下,基于LQR的主动控制、MR阻尼器的半主动控制和高阻尼橡胶支座的被动控制的位移减振率Ri值。图2～图5是在EI-Centro波激励下的体系位移响应时间历程。数值结果分析表明:

(1)3种控制方法都具有一定的减振效果,其中效果最好的是主动控制,其次是M R半主动控制和高阻尼橡胶支座的被动控制。

(2)对于不同的地震波,主动控制和MR半主动控制均能达到不同程度的控制,而同一高阻尼橡胶支座的被动控制效果有明显的差异。这是因为在被动控制中,由于结构之间的相互作用而又没有其它系统外能量的输入,某一部分的结构得到控制之后将会影响其它结构的控制。对于不同的地震激励,这种影响程度是不同的,所以会导致同一高阻尼橡胶支座的被动控制效果有明显的差异。

(3)从体系的结构来看,刚度较大的墩的控制效果不如刚度较小的墩。

图2 不同控制策略下主梁的位移响应时间历程

图3 不同控制策略下1#墩的位移响应时间历程

图4 不同控制策略下2#墩的位移响应时间历程

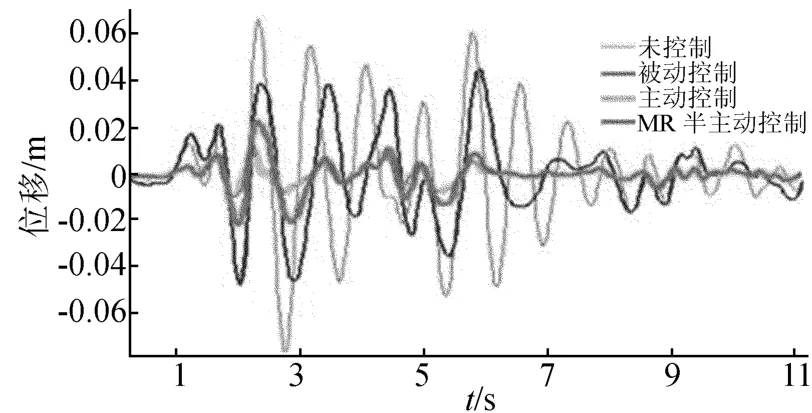
图5 不同控制策略下3#墩的位移响应时间历程

5 结束语

在土木工程应用中,主动控制的控制力在任意时刻都可以取到最优值是不现实的,但可以通过MR半主动控制设备尽可能地接近最优值,以达到比较理想的控制效果,这说明MR半主动控制有很强的实用性。

本文根据高架桥梁的动力特性,以实际高架桥的多自由度体系为研究对象,分析了3种地震激励下系统在MR阻尼器半主动控制时的水平位移控制效果,并与被动控制、主动控制效果进行了比较。研究表明,MR阻尼器的半主动控制能够有效地减小高架桥的水平位移地震反应,明显优于被动控制,且接近于主动控制。

[1] 张俊平,李新平,周福林.桥梁结构振动控制发展及存在的问题[J].世界地震工程,1998,14(2):9-16.

[2] 李忠献,姜 南,徐龙河,等.不同控制策略下安装磁流变阻尼器的模型结构振动台试验与分析[J].建筑结构学报,2004,25(6):15-21.

[3] Dyke S J,Spencer B F,Sain M K,et al.M odeling and control of magnetorheological damper for seismic response reduction[J].Smart M ater and Struct,1996,5(5):565-575.

[4] Kawashima K,Unjoh S.Seismic response control of bridge by variable dampers[J].J Struct Eng,ASCE,1994,120(9):2583-2601.

[5] Symans M D,Kelly S W.Fuzzy logic control of bridge structures using intelligent semi-active seismic isolation sy stems[J].Earthquake Eng Struc Dyn,1993,22:833-854.

[6] 陈水生.高架桥梁M R半主动控制研究[J].长安大学学报:自然科学版,2003,23(6):40-43.

[7] Spencer B F,Dyke S J,Sain M K,et al.Phenomenological model for magneto-rheological dampers[J].J Engrg M ech,ASCE,1997,123(3):230-238.

[8] 欧进萍.结构振动控制:主动、半主动和智能控制[M].北京:科学出版社,2003:62-63.