非磁性圆柱导体半径和电导率差动式涡流测量方法的研究

杜向阳, 程武山, 范狄庆, 余 遒

(1.上海工程技术大学机械工程学院,上海 201620;2.上海工程技术大学 电子电气工程学院,上海 201620)

0 引 言

本文利用圆柱形导体件涡流磁场分布的相关理论,引用通用参数﹒n推导出用于测量非铁磁性圆柱导体材料的半径a和有效电导率σ的数学公式,通过微分方法建立了半径和有效电导率相对增量的等式,进而建立了测量非铁磁圆柱体导体被测件半径a和有效电导率σ的差动式涡流检测的数学模型。

通过实验对非磁性圆柱导体半径和电导率差动式涡流测量方法进行了初步的研究。

1 工作原理

利用文献[1-5]中的关于圆柱形导体件涡流磁场分布的相关结论,引用通用参数﹒n来推导非铁磁性圆柱导体材料(相对磁导率μr≈1)a和σ的数学公式。

建立﹒n的模N与其相角φ的公式为:

其中,E2为有被测件放置时,涡流传感器的总电动势;E0为在空载情况下涡流传感器的电动势;η为填充系数,其表达式为:

其中,a为圆柱导体被测件的半径;an为传感器工作线圈的半径;μ2为复合的有效磁导率,且根据贝塞尔定理可以得出:

其中,I0、I1分别为贝塞尔函数第0、1级虚数变量[6,7],X为综合参数,计算公式为:

其中,μ0为真空磁导率,4π×10-7H/m;ω为角频率,ω=2πf,f为测量磁场频率;μr为非磁性材料的相对磁导率,μr≈1。

通过(1)式、(3)式得到导体半径公式为:

由(5)式得到有效电导率公式为:

把X的相对增量分子分母上下同乘以δ φ/φc,经过转化得:

把N的相对增量分子分母上下同乘以δ X/Xc。经过转化得:

其中,φc、Xc、Nc为差动检测方式中参照物的参数。

对(6)式、(7)式求导,并把(8)式、(9)式代入,得到半径和有效电导率相对增量的等式为:

其中,E2c为参照物产生的传感器电动势;δ E2为电动势增量,即被测件和参照物参数相互之间的差异;A、B为影响系数,计算公式为:

由此,可以推导出利用差动的方法获得被测件的半径a和有效电导率σ的公式,即

2 差动式涡流检测方案

测量圆柱导体相对磁导率 μr和半径a的装置如图1所示[8]。

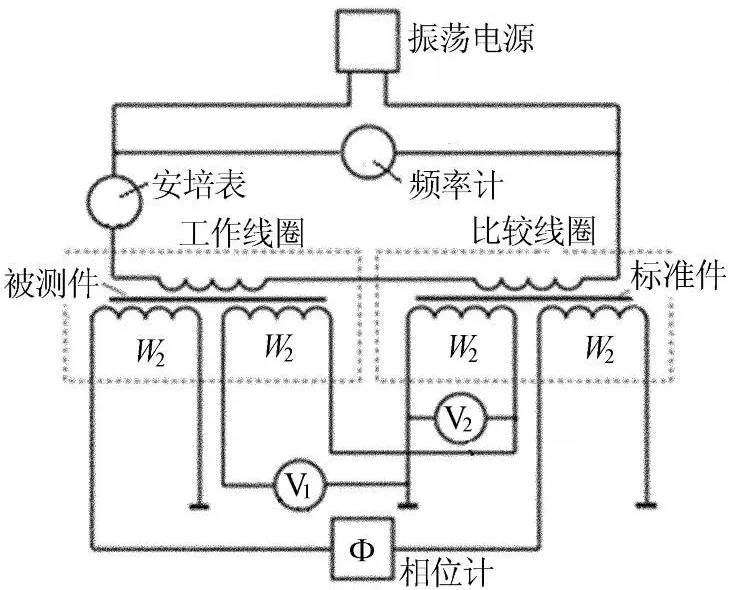
图1 差动式双参数涡流传感器电路图

该装置使用了2组相同的通过式感应线圈(工作线圈和补偿线圈),这些线圈组中的磁化线圈中的电流为正弦电流,电流的频率由振荡电源中的振荡器产生。工作线圈和平衡线圈中的测量线圈的圈数是完全相同的(W2),这些线圈的内部放置被测工件和标准件。另外装置还使用了伏特表V1、V2和相位计 Φ。

把与被测件直径相同的标准件放置在比较线圈内部,把被测件放置在测量线圈内部以后,就可以从伏特表 V1、V2和相位计 Φ上得到E2c、δ E2和φ2这3个相应的电信号值,然后把电信号带入(10)式、(11)式中,就可以计算出被测件电导率和半径相对于参照物的相对增量值,再通过(12)式、(13)式计算出被测件的实际电导率和半径值。

3 实验验证

以图1所示的差动式涡流传感器装置为测量装置,选非磁性的不同半径和电导率的铜合金为被测量件,利用(10)～(13)式,按照设计的测量方法对测量的电信号进行a和σ的推导计算。测量计算的结果见表1所列。

表1中,a和σ为计算值,对应的计量值为a′和 σ′;参照物是铜:ac=1.9 ×10-2m,σc=5.7 ×107s/m;1/E2c=42.821 6 V-1;A=-0.013;B=-0.066;选择工作点 X0=2;φ0=56.74。

实验表明,用差动式涡流传感器对于参照物性质相差不大的被测物的半径和有效电导率的测量具有一定的精度。随着材料特性差异的增高,测量误差呈升高趋势。

表1 差动式涡流传感器测量铜合金a和σ的结果

[1] А б р ам о в и ц а М.С т и г ан И.П р а в о ч н и к П оС п е ц и а л ь н ы м Ф у н к ц и я мсФ о р м у л ам и, Г р аф и к ам и, Т а б л и ц ам иП о дР е д[M].Мо с к в а :Н а у к а,1979:283-285.

[2] Я н к е М, Э м д еФ, Л е ш Ф.С п е ц и а л ь н ы еФ у н к ц и и[M].Мо с к в а:Н ау к а,1977:340.

[3] А в р ам е н к оА А, Г о р к у н о вБ М, С е б к оВ П.М е т о д и к а Р а с ч ё т а С и г н ал о в Э л е к т р о м а г н и т н о г о П р е о б р а з о в ат е л яс Ц и л и н д р и ч е с к и мИ з д е л и е м[J].П р и- б о р о с т р о е н и е,1986,4:64-67.

[4] С е б к о В П, А в р ам е н к о А А, Д р у н о в В А.И з м е р е н и е У д е л ь н о йЭ л е к т р и ч е с к о й П р о в о д и м о с т иЦи л и н-д р и ч е с к и х И з д е л и й[J].Д е ф е к т о-с к о п и я,1984,(6):79-84.

[5] Д в ай тГБ.Т а б л и ц ыИ н т е г р ал о в иД р у г и еМ а т е м а т и ч е с к и е Ф о р м у л ы[M].Мо с к в а:Н ау к а ,1978:228.

[6] 杜向阳,张永宇,范迪庆.圆柱导体双参数涡流检测技术的研究[J].无损检测,2007,29(9):509-511.

[7] С е б к оВ П, Д уХ Я.Д и ф ф е р е н ц и а л ь н ы й Д в у х п а р а м е т р о в ы й Э л е к т р о м а г н и т н ы йП р е о б р а з о в а т е л ь[J].В е с т н и кХ а р ь к о в-с к о г о Г о с у д а р с т в е н н о г о П о л и т е х н и- ч е с к о г о У н и в е р с и т е т а,1999,24(61):78-84.

[8] 杜向阳,何法江,王明红,等.圆柱导体的双参数差动式涡流检测技术的研究[J].无损检测,2007,29(11):660-662.