基于量子粒子群优化算法HAPF参数的多目标优化

张国荣, 李 丹

(合肥工业大学教育部光伏系统工程研究中心,安徽合肥 230009)

0 引 言

社会的发展和科技的进步使电力电子装置得到广泛的应用,电力系统中的谐波污染随着非线性负载数量和容量的增加日趋严重,往往使电网的波形产生严重的畸变。任何暂态和瞬态的电能质量问题都可能造成电力设备运行的异常或损坏,从而影响工矿企业的正常生产,造成巨大的经济损失。因此,电能质量的综合治理问题亟待解决,成为近年来社会关注的热点之一。

无源滤波器(passive power filter,简称PPF)和有源电力滤波器(active power filter,简称APF)相结合的装置——混合型有源电力滤波器(hybrid active power filter,简称 HAPF),有效地综合了PPF和APF的优点,成为谐波治理和无功补偿一体化系统的发展方向。HAPF利用PPF分担APF的一部分补偿任务,减小APF的容量、降低成本,使整个系统具有良好的性能[1]。小容量的APF和大容量的PPF相结合是目前研究的主流。两者的参数匹配和容量的分配问题决定着HAPF系统的实用性和经济性,是一个具有重要现实意义的研究课题。

目前,HAPF的设计方法一般是根据工程经验和简单的技术指标来选择参数,没有进行优化设计。现有的优化设计方法目标比较单一,寻优空间小、寻优能力不强[2],或者对PPF多目标优化,而未考虑PPF参数对APF的影响。惩罚函数的方法较难兼顾各目标获得有效解[3],大部分多目标优化算法是基于遗传算法(genetic algorithm,简称GA)的,但是遗传理论相对比较复杂,包括选择、复制、交叉及变异等过程。

粒子群算法(particle swarm optimization,简称PSO)是一种基于群智能的方法,源于对鸟群觅食行为的仿真[4,5]。PSO算法将每个个体看作是在N维搜索空间中的一个没有质量和体积的微粒,能够调整自身的运动轨迹,同时向着自己和其它微粒曾经经历过的最优位置飞行。PSO算法比遗传算法简单、易于实现,但具有较容易陷入局部极值点、不向最优解方向进化的缺点。

2004年,Sun等人从量子力学的角度出发,提出了一种新的PSO算法模型,该方法将量子理论引入粒子群算法,认为粒子具有量子行为[6,7]。量子的多态性、叠加性、纠缠性等与粒子群算法的全局寻优能力结合起来,具有比传统的粒子群算法更高的效率[8]。

本文的量子粒子群优化算法(quantum-behaved particle swarm optimization,简称 QPSO)采用量子门的旋转角作为粒子的位置,粒子群算法作为量子旋转门的更新策略,使算法能探索不同的区域,更新种群的同时,也能防止陷入局部最优造成早熟收敛[9]。

另外,用动态惯性权重法来平衡粒子群算法对解空间全局和局部的搜索能力,解决HAPF参数匹配以及无源部分和有源部分容量的合理分配问题。

1 并联混合有源电力滤波器的结构

本文讨论的并联混合有源电力滤波器(SHAPF)是指APF与PPF串联之后并入电网的拓扑结构,其结构示意图如图1所示。并联混合有源电力滤波器由APF、PPF(包括单调谐滤波器和高通滤波器)、输出滤波器和隔离变压器4部分组成。

图1 并联混合型有源电力滤波器结构图

本研究中电网的特征次数谐波主要为(6k±1)次,其中5次和7次谐波含量较大,故PPF由5次单调谐滤波器和7次单调谐滤波器构成,如果电网中其它次数的谐波电流含量也较大,可以增加其它次数的单调谐滤波器。APF采用电压型逆变器滤除电网部分谐波,并抑制电网阻抗与PPF之间谐振。输出滤波器用LC低通滤波器滤除开关器件产生的高频毛刺[10]。

2 优化目标描述

APF容量占HAPF总容量的百分比m为:

使系统功率因数尽量接近1,且不出现无功过补偿,即

其中,Q为PPF的基波无功功率,Q在PPF的基波无功功率的上、下限范围内变化;Qi为滤波各支路的基波无功功率;i为各支路调谐次数。

电网谐波含量低于一定限制,符合国家标准,电流、电压的总谐波畸变率为系统滤波效果衡量标准。以电流、电压的总谐波畸变率作为优化目标的要求,计算公式为:

其中,THDI、THDU分别为系统的电流、电压总谐波畸变率;Ih、Uh为系统h次谐波电流、电压有效值;I1、U1为系统基波电流、电压有效值;ηIhmax、ηUhmax分别为h次电流、电压畸变率允许的上限;N为截取的谐波最高次数,通常取N≤25。

HAPF参数的优化设计问题综合考虑了HAPF投资成本、滤波效果和无功补偿等因素,是3个优化目标函数取得协调满意解的搜索问题。其中,PPF的设计原则遵守PPF在工程应用中的一般性设计准则[11]。本文提出一种量子粒子群优化算法,综合考虑HAPF投资成本滤波效果、无功补偿等因素,解决系统的参数匹配以及无源、有源容量分配的优化设计问题。

3 基于QPSO的SHAPF参数设计

3.1 量子角的表示

定义 一个量子角为一任意角度值θ,则一个量子比特可以由量子角表示为[θ],等价为原有量子比特,表示为sin θ和 cos θ分别表示相应态的概率振幅;|sin θ|2表示量子比特“0”态时的概率;|cos θ|2表示量子比特“1”态时的概率, 且自然满足|sin θ|2+|cos θ|2=1。

此时一个量子比特可以由量子角表示为通用量子旋转门调整策略,公式为:

3.2 量子粒子群算法

量子粒子探索多维空间,在每一轮迭代中评价自身的目标位置(适应值),找到每次迭代过程中的局部最优量子角和全局最优量角,用量子旋转门对量子角进行动态调整以更新自己的速度和位置[13],不断地比较和追随候选的空间解,最终发现最优解或者局部最优解。具体操作为:量子粒子i的第j比特在第t次迭代时的速度、位置、个体和全局最优位置分别为,则速度和位置的迭代公式为:

w称为惯性权重,是与前一次速度有关的比例因子,用w控制前次的速度对当前速度的影响。在搜索过程中,全局搜索能力与局部搜索能力的平衡对于算法的成功起着至关重要的作用[14]。惯性权重类似模拟退火中的温度,较大的w有较好的全局收敛能力,适于对解空间进行大范围探查,而较小的w则有较强的局部收敛能力,适于进行小范围开挖。因此,随着迭代次数的增加,w惯性权重应不断减少,动态下降的惯性权重计算公式为:

其中,wmax、wmin分别为w惯性权重的最大值和最小值;max N为最大截止代数;t为当前迭代次数。

在文献[15]中,惯性权重 w满足w(t)=0.9-0.5t/max N。将惯性权重看成迭代次数的函数,w可从0.9到0.4线性减少。本研究中的惯性权重w,按照(7)式计算。

粒子的速度可以表示为同一个量子粒子t代和t+1代的距离或差异。根据(5)式可以看出,粒子速度的更新按照以下3部分进行:

(1)量子粒子速度学习自身的历史信息wvij(t)称为动量部分,是量子粒子以一定的概率接受自身速度的信息。

(2)量子粒子速度从个体最优位置获得信息。c1rand()(-θij(t))称为个体认知部分,鼓励它飞向自身曾经发现的最优位置,表示以一定的概率吸收了量子粒子个体最优位置和量子粒子本身的差异信息。

(3)量子粒子速度从全局最优位置获得信息。c2rand()(-θij(t))称为社会认知部分,引导粒子飞向量子粒子群中的最优位置,表示以一定概率吸收了量子粒子全局最优位置和量子粒子本身的差异信息。

3.3 适应度函数

适应度函数是指根据问题需要,按照一定的策略评价粒子(问题潜在解)的优劣。算法停止时,适应度函数最优的粒子即为优化搜索的最优解[16]。采用线性加权的方法给出综合适应度函数:

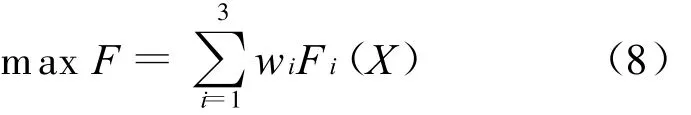
为了方便处理,先对目标函数m、Q、THDI统一量纲,各个单目标的归一化目标满意函数为F1、F2、F3,变化范围均为0～ 1.0,wi为对应的权重,i=1,2,3,这样就转化成能综合反映全体优化目标的单目标优化问题,归一化满足函数的关系如图2所示。

图2 归一化满意函数与其目标函数的关系

3.4 算法流程

算法计算步骤如图3所示。

图3 量子粒子群多目标优化算法流程

4 算例分析

某变电站10 kV母线处,主要的电流谐波为5次、7次,具体各谐波含量见表1所列,A相电流波形如图4所示。该变电站的三相电压平均总畸变率为4.7%,三相电流平均总畸变率为6.8%,功率因数为0.82。故装设5次、7次单调谐滤波器和二阶高通滤波器各1组,3相共12组,其中,高通滤波器截止频率为500 Hz。单调谐滤波器品质因数Q一定,各滤波器支路电容量作为独立优化变量,同时考虑5%的背景谐波。适应度函数的各权重系数为:

表1 滤波前各次谐波含量

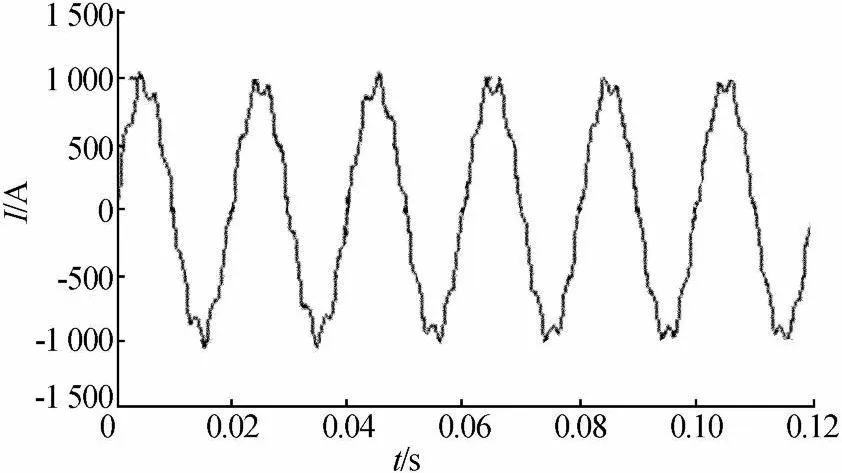
图4 滤波前的A相电流波形

采用标准遗传算法(standard genetic algorithm,简称SGA)和QPSO分别对SHAPF系统的m、Q、THDI参数进行优化。设计发现,QPSO进化到第50代左右时,即可获得满意解,而SGA收敛速度明显慢于QPSO,第175代左右可得到满意解,如图5所示。且前者没有QPSO编程简单,程序占用的计算机内存较大。2种多目标优化算法的设计结果见表2所列,从表2可以看出,本文的QPSO比SGA提供了更多的无功补偿,电压总谐波畸变率和电流总谐波畸变率也均略低于SGA。这说明QPSO收敛速度较快、全局寻优能力较强,更容易在探索与开发之间取得平衡,弥补了SGA容易早熟的不足。

图5 目标适应度值的进化过程

根据量子粒子群算法的优化设计结果,进行仿真和实验,仿真得到滤波后A相电流波形如图6所示,与图4相比波形少了很多毛刺,更接近于正弦波。从表1可看出,滤波前的谐波含量比低次谐波有明显的降低,由此可看出量子粒子群算法的有效性。

表2 遗传算法和量子粒子群算法的优化设计结果

图6 滤波后的A相电流波形

5 结束语

在粒子群算法的基础上,本文应用一种量子粒子群多目标优化方法对HAPF参数进行优化,解决HAPF参数匹配、无源和有源容量的合理分配问题,降低了系统的初期投资。该算法相对简单,寻优能力较强,滤波效果良好,满足无功补偿要求,使HAPF在电能质量综合治理中达到既有效又经济的双重目的。

[1] 刘凤君.市电电能质量补偿技术[M].北京:科学出版社,2005:113.

[2] 马大铭,朱东起,谢 磊.综合电力滤波系统中无源滤波器的设计[J].电工电能新技术,1997,16(3):1-4.

[3] 陈峻岭,姜新建,朱东起,等.基于遗传算法混合有源滤波器参数的多目标优化[J].清华大学学报:自然科学版,2006,46(1):5-8.

[4] Vishwanathan S V N,Smola A J,Murty N M.Simple SVM[C]//Proc of the Twentieth International Conference on M achine Learning,Washing ton,D C,USA,2003:760-767.

[5] Yang Xiaowei,Lin Daying,Hao Zhifeng,et al.A fast SVM training algorithm based on the set segmentation and K-means clustering [J].Progress in NaturalScience,2003,13(10):750-755.

[6] Joachims T.Making large-scale SVM learning practical[C]//Kernel Methods:SupportVectorLearning.Cambridge:MIT Press,1999:169-184.

[7] Platt J.Fast training of support vector machines using sequential minimal optimization[C]//Kernel Methods:Support Vector Learning, Cambridge:MIT Press,1999:185-208.

[8] 许 坤.基于量子衍生方法的粒子群多目标优化算法[D].长沙:湖南大学计算机与通信学院,2008.

[9] 李 栋.量子衍生多目标进化方法及其应用[D].长沙:湖南大学计算机与通信学院,2008.

[10] 罗 安.电网谐波治理和无功补偿技术及装备[M].北京:中国电力出版社,2006:81.

[11] 王 岩,路春一.一种新的量子群进化算法研究[J].小型微型计算机系统,2006,27(8):1479-1482.

[12] Das J C.Passive filters:potentialities and limitations[J].IEEE Trans on Industry Application, 2004, 40(1):232-241.

[13] Zhang T,Ramakrishnan R,Livny M.BIRCH:an efficient data clustering method for very large databases[C]//Proc ACM SIGMOD Int Conf Management of Data,1996:103-114.

[14] 何 娜,黄丽娜,武 健,等.基于粒子群优化算法的混合有源滤波器中无源滤波器的多目标优化设计[J].中国电机工程学报,2008,28(27):63-69.

[15] Shi Y,Eberhart R C.Empirical study of particle swarm optimization[C]//Proceedings of the 1999 Congress on Evolutionary Computation.Piscataway,NJ:IEEE Service Center,1999:1945-1950.

[16] 陈永刚,牛丹梅,范庆辉.粒子群算法在组合优化问题上的研究与发展[J].电脑与电信,2008,(12):41-43.