均值—CVaR优化模型在投资组合中的应用

王晶,张裕生,王玉玲

(1.蚌埠学院数学与物理系,安徽蚌埠 233000;2.天津商业大学理学院,天津 300134)

均值—CVaR优化模型在投资组合中的应用

王晶1,张裕生1,王玉玲2

(1.蚌埠学院数学与物理系,安徽蚌埠 233000;2.天津商业大学理学院,天津 300134)

本文从CVaR风险度量方法的理论出发,建立了符合我国证券市场的均值—CVaR投资组合优化模型,并对模型进行了理论分析.本文还通过实证研究得出了均值—CVaR模型的有效边界,结果证明了CVaR模型控制风险的有效性.

CVaR;投资组合;有效前沿;风险＊

1 CVaR的定义

CVaR是Conditional Value at Risk的简写,译为条件风险价值.它作为一种金融风险度量工具由Tyrrell Rockafellar和Stanislav Uryasev于1999年首次提出.

设L(X,Y)是损失函数,其中x∈Rm为决策向量,X为可行集,y∈Rm为一随机向量.例如x可理解为风险资产的组合系数,X为所有可能组受各种约束合的集合,当然也可根据具体情况做其它解释.y代表能影响损失的市场不确定性.当损失为负时,意味着有正的收益.若y的概率密度为p(y),则对任给x,损失L(x,y)的分布也随之确定,其分布函数为:

而相应的在概率置信水平β(0<β<1)下,损失β-V aR和β-CV aR分别定义为:

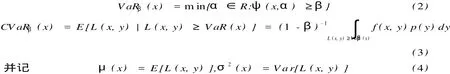
对资产组合而言,收益R(x,y)和损失L(x,y)分别为:

其中x=(x1,x2,…,xn)T,且xj=xTI,I=(1,1,…,1)T,y=(y1,y2,…,yn)T,yj代表第j种金融工具的回报率,j=1,2,…,n.这时可行集为X={x∈Rn:xTI=1}.

因为损失、收益的货币单位与百分比之间存在一一对应的线性关系,所以我们把V aR、CV aR的度量单位折算为初始价值的百分比.

若设E(y)=μ,C ov(y)=V,则收益、损失的均值和方差分别为:

因此得到基于CV aR的证券组合优化:

或者m in

其中:Rp=xTR——投资组合的期望收益率,R=(R1,R2,…,Rn)——投资组合中资产的收益均值,x=(x1,x2,…,xn)T——投资组合中各资产所占的比例,R0——投资者期望收益率.

2 实证研究

我们从上海证券市场选择了5种具有代表性的股票:东方航空,上海石化,第一百货,清华同方,陆家嘴.这些股票数据来自2003年1月2日到2004年8月8日.我们使用计算机软件分别计算了这5种有价证券在95%置信水平下的:均值—方差、V aR、CV aR,并且分别绘制了这三种模型的有效前沿图.

下面我们给出一个例子来说明这三种优化问题是等价的.设定置信水平为95%, c1(β),c2(β)已知.由于证券的在此风险下的安全收益率满足标准正态分布,由此可得μ(x)和σ(x).由公式

和

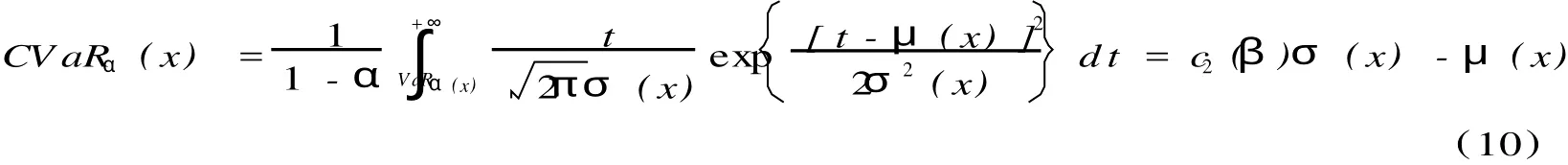
我们可计算出V aR和CV aR.

以下是通过exce l软件和m a tlab软件计算得出的结果.

表1 均值/方差/V aR/CV aR最优投资组合(置信度95%)

此表显示的是不同日期的股票的最优组合和在此组合下三种不同约束条件的收益,明显可以看出,在CV aR条件下对风险的预期是最大的,这充分说明了CV aR预测了投资组合的潜在风险,从而证明CV aR比其他风险预期更加谨慎.表中投资组合中权重存在负值情况,表示可以卖空.

表2 最优化组合后的风险价值和一致风险价值(置信度95%)

由上面的结果可以发现,最小化CV aR后的投资组合是非常理想的.并且CV aR值所度量的风险值仍然大于V aR值,从而符合V aR和CV aR的定义,保证了它们的合理性.

下面是三种模型的有效前沿分析图和一个三种模型的综合图:

图1 均值—方差模型的有效前沿

图2 均值—VaR模型的有效前沿

图3 均值—CVaR模型的有效前沿

图4 三种有效前沿组合图

图1、图2、图3分别给出了在正态分布下均值—方差、均值—V aR、均值—CV aR模型的有效前沿,其中纵坐标为收益,横坐标分别表示标准差、V aR和CV aR.而图4是以上三种图形的组合图.从图中可以看出,在收益确定的条件下三种模型的资产组合解相同,且CV aR大于标准差和V aR.

均值—方差模型给出了投资组合的标准差,比较来看,均值—CV aR模型下限收益率高,说明在CV aR条件下比另外两种约束条件更能体现投资组合的潜在损失.其次,从图4从所得到的有效边界的上限来看,用CV aR作为约束条件得到的收益率略小于另两种方法的收益率,说明CV aR作为约束条件比其他方法更为保守和安全.

3 结论

总体来看,CV aR与V aR、方差相比,收益率上限低于其他两种方法,而下限略大于另两种方法.这表明CV aR作为约束条件使投资组合的有效边界减小了,从而证明了CV aR更能体现投资组合的潜在风险:损失直观、简洁,容易理解,更接近投资者的心理习惯,因此CV aR比其他模型更符合实际.

[1]RobertA Jarrow,StuartM Turnbu ll.The intersection ofm arker and credit risk[J].JournalofBanking&Finance,2000. (24):271-299.

[2]J PM o rgan.R isk M etrics.TechnicalDocum ent[M].1996:17-25.

[3]A rtzner P,Delbaen F,Eber JM,Heath D.Coherentm easuresof risk[J].M athem atical Finance.1999.9(3):203-228.

[4]M auser H,Rosen D.Beyond VaR:from m easuring risk tom anaging risk.AL GO Research Quarterly[J].1999.1(2):5 -20.

[5]M arkow itz H M.Po rtfo lio selection[J].Jou rnalof Finance.1952,7(1):77-91.

[6]SharpW.Cap italA sset Prices:A theory of cap italM arket Equilibrium under conditions of risk[J].Journal of Finance, 1964(19):425-442.

[7]Thom as F.Co lem an,Yuying L i.M inizing CVaR and VaR fora Portfo lio ofDerivatives[J].GainesvilleM arch,2004(5):57 -58.

[8]封建强,沪深股市收益率风险的VaR侧度研究[J].统计研究,2002(4):34-38.

[9]陈剑利,李胜宏.VaR风险度量模型在投资组合中的运用[J].运筹与管理,2002.(2),95-99.

[10]A lexander GJ,Bap tista A M.Econom ic imp lications of using aM ean-VaR model for portfo lio selection:a comparison w ithm ean-Variance analysis[R].University ofM innesota,2000.

[11]程盛芝.金融市场风险测量的VaR方法及其应用[J].商业研究,2002.

[12]陈金龙,张维.CVaR与投资组合优化统一模型[J].系统工程理论方法应用,2002(1):68-71.

[13]R.Tyrrell Rocka fellar,Stanislav Uryasev[J].Optimization of Conditional Value-at-Risk.Journal of Risk,2000,2:21 -24.

[14]刘小茂,李楚霖,王建华.风险资产组合的均值-CVaR有效前沿[J].管理工程学报,2003,(1):29-33.

[15]林旭东,巩前锦.正态条件下均值-CV aR有效前沿的研究[J].管理科学,2004,(6),52-55.

[16]马超群,李红权.VaR方法及其在金融风险管理中的应用[J].系统工程,2000,(2):56-59.

F830.59;F224.0

A

1004-7077(2010)02-0041-04

2009-12-16

安徽省高等学校省级自然科学研究项目(KJ2009B213)

王晶(1981-),女,湖北广水人,蚌埠学院数理系讲师,主要研究方向为金融数学与金融风险管理.

[责任编辑:陈庆朋]