杨氏双缝干涉条纹移动问题的探讨
2010-10-23古丽姗
古丽姗
(昌吉学院物理系,新疆昌吉 831100)
杨氏双缝干涉条纹移动问题的探讨
古丽姗
(昌吉学院物理系,新疆昌吉 831100)
本文以杨氏双缝干涉实验为研究对象,分析了中央明纹和介质对干涉的影响,得到屏上干涉条纹移动的原因,找到一种快速简便处理问题的途径.
杨氏双缝干涉;介质;光程差;条纹移动*
0 引言
1801年,杨氏巧妙地设计了一种把单个波阵面分解为两个波阵面以锁定两个光源之间的相位差的方法来研究光的干涉现象.杨氏用叠加原理解释了干涉现象,在历史上第一次测定了光的波长,为光的波动学说的确立奠定了基础.
在杨氏双缝干涉实验中,在不加介质或不将整个装置浸入透明液体中之前,两相干光均在空气中传播,他们到达屏上任一点P的光程差由其几何路程差决定,而在插入介质片或将整个装置浸入透明液体中后,虽然两相干光在两介质薄片中的几何路程相同,但光程却不同,因此,在杨氏实验中,分析干涉条纹的位置、形状、条纹间距及走向,尤其是分析干涉条纹的移动是一个重点,也是难点.杨氏双缝干涉问题中的光程差的分析和计算都是把对中央明条纹的位置判断作为问题的焦点,但是在具体运用中,稍有不慎就特别容易出错.因此本文通过杨氏干涉实验中,如上下微小移动狭缝或点光源),狭缝前或后盖介质片和将整个装置浸入透明液体中等时,分析讨论屏上干涉条纹移动的情况寻求条纹移动的规律,并对在分析问题中易出现的错误,利用规律分析出现该错误的原因,从而得到一种避免该错误的方法,即找到一种快速简便处理问题的途径.
1 中央明条纹对双缝干涉的影响
在双缝干涉中,中央明条纹的位置判断成了问题的焦点.我们知道,光是横波,传播的过程中将出现波峰和波谷,在两列相干波相互叠加的区域,波峰、波峰或波谷、波谷相遇处将出现明条纹,波峰波谷相遇处将出现暗条纹.如图1所示,当单缝S从双缝的S1,S2中央对称轴位置处稍微向上移动时,如果刚好移动到单缝到S双缝S1,S2的光程相差半波长的奇数倍,即Δ=(2κ+1)(k=0.±1.±2…)时,屏上P处出现暗条纹;如果单缝到S双缝S,S的光程相差半波长的偶数倍,即相位差为Δ=2k(k=0,±1,±2…)
12时,屏上P处出现明条纹.从上面的分析我们看到,光屏上P点出现的是暗条纹还是明条纹,将受到单缝S所处位置的影响.显然,对于光屏上的原中央点O来说,也将随单缝S的上移或下移,出现明暗条纹交替现象.当单缝到S双缝S1,S2的光程相差为波长的整数倍时出现明条纹,为半波长的奇数倍时出现暗条纹.如果R1≠R2,这时S发出的两束相干光到屏上O点处的光程差为Δ=r2-r1+R2-R1,由图可见,由S发出的光到达S1,S2的光程相同,此时R1=R2且r1=r2,因此,这两束相干光将传到屏上中央O处,其光程差Δ= 0,形成明条纹,称之为中央明条纹.然而,当光源S移到S′时,由于R1≠R2中央明条纹将从O点移到点P处,P点的位置由零程差(Δ=0)决定,那么,这时应有:Δ=r2-r1+R2-R1=0或R2-R1=r1-r2.当点光源向负y方向平移即向下平移时,R1>R2,零程差要求r2>r1,,此时干涉条纹应向y正方向平移.反之,当点光源向y正方向平移时,干涉条纹必然向y负方向平移.由于屏上各条纹位置只是向上或向下平移,因此条纹间距不变.由以上分析可见,S下移时,中央明条纹向上平移,那么干涉条纹将整体向上平移,S上移时,中央明条纹下移,干涉条纹将整体向下平移,但条纹间距不变.由以上分析也得到了一种探讨干涉条纹移动的方式:探讨干涉条纹移动的方向,最简单的方式是观察干涉场中一固定点(中央亮点),有多少条纹移过,或跟踪干涉场中某一级条纹(中央明条纹),看它朝什么方向移动,移动了多少距离.
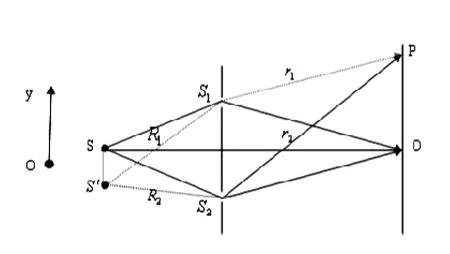
图1 “中央明条纹”对双缝干涉的影响
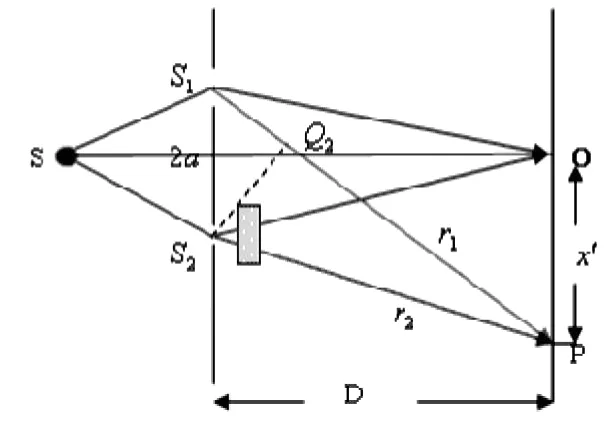
图2-1 媒质变化对双缝干涉的影响
2 介质变化对双缝干涉的影响
2.1 用透明介质折射率为n(n>1)的介质片遮缝S2
如图2-1所示,由之前分析可知,在S2处未加介质片之前,两相干光均在空气中传播,他们到达屏上任一点P的光程差Δ由其几何路程差δ决定,对于点O,光程差Δ=δ,故点O处为中央明条纹,其余条纹相对于点O对称分布.而在插入介质片后,虽然两相干光在两介质薄片中的几何路程相同,但光程不同,对于点O,此时Δ≠0,故点O不再是中央明条纹,中央明条纹为保持其光程差为零,而平移到点P,此时整个干涉条纹发生平移.此时,两束相干光在P处产生的光程差为:Δ=(n-1)d+r2-r1,为了满足中央明条纹光程差的条件即:Δ=0.从而可得,(n-1)d+r2-r1=0⇒(r1-r2)=(n-1)d⇒S1Q2=-(n-1)d,考虑到n>1⇒S1Q2<0,于是中央明条纹应当向下平移,因而杨氏双缝干涉中干涉条纹整体向下平移.下移距离及级数变化可由下式求出:S Q=kλ′.,S Q=1212可见k′<0,x′<0与上述分析结果一致.
2.2 用透明介质折射率为n(n>1)的介质片遮上缝S1
如图2-2所示,双缝未插入玻璃片前,中央明条纹出现在O点,插入玻璃片后,中央明条纹出现在P点,此时的光程差:Δ=r2-[(n-1)d+r1]=r2-r1-(n-1)d,由于出现中央明条纹光程差的条件是:Δ=kλ=x=0,所以由r-r-(n-1)d=0得r212-r1=(n-1)d,因为(n-1)d>0且r2-r1=S2Q2,所以S2Q2>0,又因为S2Q2=k′λ, S Q=·x′于是可得22同理分析结论为:k′>0,x′>0这说明:中央明条纹应当向上平移,即干涉条纹整体向上平移.

图2-2 媒质变化对双缝干涉的影响图

2-3 媒质变化对双缝干涉的影响
2.3 用折射率不同的两个介质片遮双缝
如图所示2-3,双缝未插入玻璃片前,中央明纹出现在O点,但当双缝分别插入折射率不同的介质片后,中央明纹出现在P点,此时的光程差:
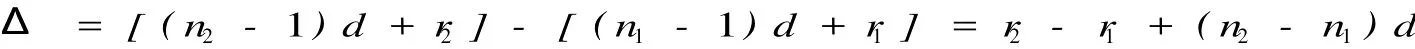
根据出现中央明条纹满足光程差的条件(Δ=0)上式应为:

分析∵n2>n1⇒r2-r1<0 即:S1Q2<0.
可见,k′<0,x′<0,这个结论说明:中央明条纹应当向下平移,亦即:干涉条纹整体应向下平移.
2.4 用折射率相同的介质片分别遮住双缝S1和S2
仿照上面的推导,我们可以得出此时中央明条纹没有移动,即k′=0,x′=0.因而干涉条纹整体不动,与装置处于真空时情况相同,也就是,中央明纹仍在屏中央,其它条纹相对与中央明纹成上下对称分布.
3 杨氏双缝干涉装置置于折射率为n的介质中
若把整个装置置于折射率为n的介质中,则:明条纹满足的光程差条件为:Δ=n(r2-r1)=kλ(k=0,±1,±2,…)暗条纹满足的光程差条件:Δ=n(r2-r1)=或者考虑:于是明条纹满足的光程差条件
4 结论
总之,通过对以上所有情况的分析论证,我们可以看到,对杨氏双缝干涉条纹移动问题的讨论所总结出来的规律对我们解决干涉问题有很大的帮助,利用这些规律也会给我们解决此类问题带来很大的方便.同时此规律对突破干涉问题的重点,难点也提供了一种简便的解决途径.
[1]钟锡华.光学题解指导[M].北京:电子工业出版社,1983:150-151.
[2]程守诛.普通物理学[M].北京:高等教育出版社,2000:173-176.
[3]马文蔚.物理学教程[M].北京:高等教育出版社,2006:188-190.
[4]马文蔚.物理学教程学习指导[M].北京:高等教育出版社,2006:236-240.
[5]赵凯华.光学[M].北京:北京大学出版社,1982:272-274.
[6]张智立.普通物理学教与学参考[M].北京:中国致公出版社,2003:205-210.
Abstract:Young’s double-slit interference experiment is studied,we analysed how the centyal-ming patterns and media affects interference fringes.The results of the reasons for interference fringes.W e found a quick and easy way to deal with the problem.
Keywords:Young’s double-slit interference,media,optical path difference,the movement of fringes
Discussion About the Movement of Fringes in The Double-slit Interference
GU Li-shan
(Department of Physics,Changji college,Xinjiang 831100,China)
TN 253
A
1004-7077(2010)02-0012-04
2009-10-17
古丽姗(1968-),女,新疆昌吉人,昌吉学院物理系副教授,主要从事光学研究.
[责任编辑:陈庆朋]
