基于随机波动模型的人民币汇率波动性分析
2010-10-18查奇芬陈风华
查奇芬,陈风华
(江苏大学财经学院统计系,江苏镇江212013)
基于随机波动模型的人民币汇率波动性分析
查奇芬,陈风华
(江苏大学财经学院统计系,江苏镇江212013)
自人民币汇率体制改革以来,汇率波动日趋复杂,对我国经济的影响也更加重要。鉴于此,文章运用随机波动(SV)模型对汇改后美元兑人民币汇率进行分析,结果表明杠杆效应对我国外汇市场的影响较小,而人民币汇率收益率与市场风险密切相关。
SV模型MCMC汇率波动
0 引言
人民币汇率时间序列同其他金融时间序列一样具有时变方差的特点,表现出波动率聚类、高峰厚尾、持久记忆等特征。由于ARMA模型不能较好的拟合此类数据,目前国内学者主要运用GARCH类模型对人民币汇率的波动性进行描述。鉴于另一类金融波动模型——随机波动(SV)模型相对于GARCH模型更符合金融理论。本文尝试运用SV模型来对汇改后人民币汇率的波动性进行分析。
1 SV模型概述
Taylor(1986)在解释金融收益序列波动模型的自回归行为提出了标准SV(stochastic volatility)模型,简称为SV-N模型,其形式如下:

其中yt表示第t日的收益率,εt为独立同分布的白噪声干扰,服从均值为0,方差为1的正态分布;ηt为独立同分布的波动的扰动水平,服从均值为0,方差为τ2的正态分布。误差项ηt与εt是不相关的,都是不可观测的。准为持续性参数,反映了当前波动对未来波动的影响,并且对于|准|<1,SV模型是协方差平稳的。潜在的波动θt服从一个持续性参数为准的高斯AR(1)过程。SV-N模型在描述金融时间序列的过程中有时显得过于简单,于是在实际运用中人们对标准SV模型进行了多种扩展,如SV-T模型、SV-MN模型、SV-MT模型、Leverage SV模型等。
尽管理论上SV模型能够较好的描述波动率的动态变化,但由于SV模型的精确似然函数很难得到,对它的参数估计有一定的困难,因此此类模型在实际应用中受到了一定的限制。然而随着Winbugs软件的广泛应用,人们使用MCMC方法模拟建立完全似然函数来近似估计模型的参数值,使得参数估计的缺点得到解决,SV模型从而得到了广泛的应用。
2 MCMC方法
马尔可夫蒙特卡罗(MCMC)方法是最近些年发展起来的一种参数估计方法。该方法将马尔可夫过程引入到蒙特卡罗模拟中实现动态模拟,以克服传统的蒙特卡罗模拟方法存在的静态性和高维性。MCMC算法的核心是对于一个给定的多元概率密度,通过反复从一个马尔可夫链中取样来产生变量,该马尔可夫链具有不变的分布。对SV模型而言,标准SV模型的似然函数表示为:f(y|θ)=乙(y|h,θ)f(h|θ)dh)。其中y包含了样本的所有观测值,h=(h1,…,hT)T是T维潜在波动向量,且θ=(α,β,ση)T包含SV模型的所有参数。从MCMC算法中取得的样本是一个高维样本,利用这些样本取样,并借助于马尔可夫链的遍历性可以进行统计推断。
3 实证分析
3.1 数据的选取
我国的汇率采用间接标价法,外汇管理局公布美元兑人民币汇率数据,其他货币兑人民币的汇率通过美元汇率数据换算而来。因此,美元兑人民币汇率数据更具有一定的代表性。本文选取了2007年11月30日至2009年11月30日共488个人美元兑人民币的日值数据(数据来源于国家外汇管理局网站:http://www.safe.gov.cn/model_safe/index.html)。对原始汇率数据序列取对数,再进行一阶差分得到人民币汇率的日对数收益率序列YU。应用Eviews6.0软件得到汇率收益率序列的基本统计特征,如图1所示。
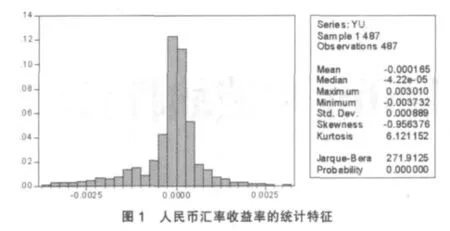
由图1可知,人民币汇率的日收益率序列的偏度为-0.956376,峰度为6.121151(大于3),人民币日收益率序列呈现明显的尖峰厚尾的分布特征,且Jarque-Bera统计量也在99%以上的置信水平上拒绝序列为正态分布的假设。
对人民币汇率的日收益率YU进行平稳性检验,检验结果如表1所示。
由表1可知美元兑人民币汇率收益率序列的ADF统计量的绝对值均大于各自不同显著水平下的临界值,表明该收益率序列均不存在单位根,在不同显著水平下均为平稳序列。

表1 汇率日收益率序列ADF检验
3.2 实证结果分析
针对人民币/美元汇率收益率序列,运用MCMC模拟方法和Winbugs软件对SV-N、SV-T、SV-MN、SV-MT、Leverage-SV模型分别进行模拟,得出SV模型族的参数μ估计,如表2所示。
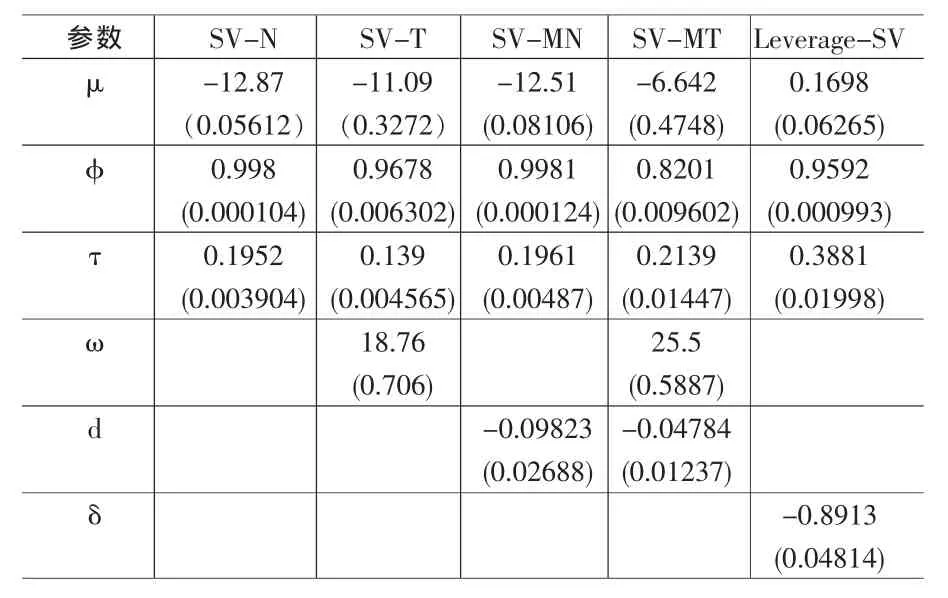
表2 SV模型族参数估计结果
通过对表2进行分析可知:
(1)对于波动水平在SV-N和SV-MN模型下的模拟值的绝对值要比其他三个模型的要大,这说明在SV-N和SVMN模型下,人民币汇率体现出更加强烈的波动性。而SV-N和SV-MN模型的参数μ的贝叶斯估计值相差不大,说明这两个模型下估计的波动水平差异不显著。
(2)五个模型的波动持续性参数准的估计值都超过了0.8,其中最大是SV-MN模型为0.9981。因此SV-MN模型能更好的刻画人民币汇率收益率序列的波动持续性。
(3)汇率波动的扰动水平通过模型的精度参数τ来度量。τ越小则说明波动过程难以预测,反之,则相反。在SV模型族中的参数τ估计值中,Leverage-SV模型τ的模拟值最大。模拟效果最好。
3.3 模型DIC准则比较分析
现有文献中关于SV模型的比较,主要是利用贝叶斯因子,但是此方法计算比较困难,因此,本文引入由Spiegelhalter等在2002年提出的DIC准则对SV模型进行比较分析,具体形式如下:DIC=+pD,其中、=Eθ|y[-21nL(y|θ)]、pD=Eθ|y[-1nL(y)]。DIC准则同时考虑了模型对数据的拟合和模型的复杂程度。其中表示了模型拟合数据的优劣,pD则衡量了模型的复杂度。值越大,则模型拟合数据越劣质;pD值越大,则说明模型越复杂。相反,则反之。
运用Winbugs软件分别求出SV模型族的值、值和值。结果如表3所示。
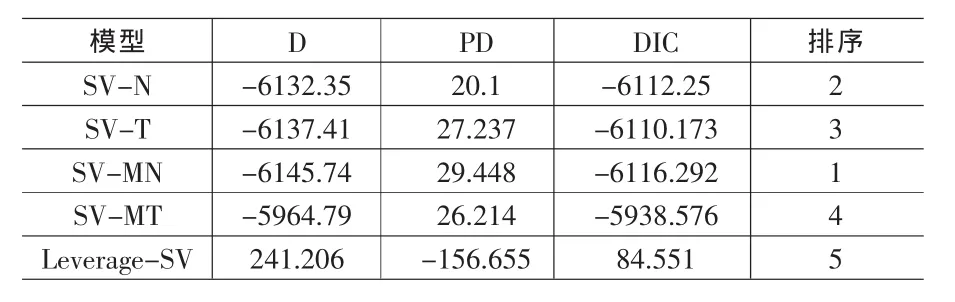
表3 DIC统计表
4 结论
本文运用随机波动模型对汇改后美元兑人民币汇率的日收益率序列进行分析,得出以下结论:
(1)五个模型的波动持续性参数的估计值都超过了0.8,人民币汇率的波动性造成的影响是持久的。
(2)SV-MN模型对人民币汇率序列拟合的效果最好,表明我国外汇市场上的汇率收益率与其所承担的风险密切相关。
(3)Leverage-SV模型对人民币汇率序列的拟合效果最差,表明“杠杆效应”在我国外汇市场上表现的不明显。
[1]Tayor,S.Modeling Financial Time Series[M].Chichester:Wiley,1986.
[2]Jacquier.E,NicholasG.Polson,PeterE.Rossi.BayesianAnalysisof Stochastic VolatilityModels[J].Journal of Business&Economic Statistics,1994(12).
[3]Gallant,A.R,D.Hsie,G.Tarchen.Estimation of Stochastic Volatility Models with Diagnostics[J].Journal of Econometrics,1997,(81).
[4]刘凤芹,吴喜之.基于SV模型的深圳股市波动的预测[J].山西财经大学学报,2004,(26).
[5]王春峰等.随机波动性模型的比较分析[J].系统工程学报,2005,(20). [6]王春峰,蒋祥林,李刚.基于随机波动性模型的中国股市波动性估计[J].管理科学学报,2003,(4).
[7]刘凤芹.基于DIC准则的SV族模型的比较[J].统计与决策,2004, (9).
[8]张世英,樊智.协整理论与波动模型:金融时间序列分析及应用[M].北京:清华大学出版社,2004.
(责任编辑/浩天)
F201
A
1002-6487(2010)22-0113-02
教育部人文社科规划基金项目(07JA910003)
