基于决策树方法的信息价值求解方法
2010-10-18王蕾房俊民
王蕾,房俊民
(中国科学院国家科学图书馆成都分馆,成都610021)
基于决策树方法的信息价值求解方法
王蕾,房俊民
(中国科学院国家科学图书馆成都分馆,成都610021)
传统的信息价值求解方法在行动选择或实验结果情况很多的情况下,步骤繁琐,计算量大,引起众多麻烦。而决策树方法是辅助行动选择的重要参考,并且在excel的宏工具容易求解。文章用决策树的思路和方法求解决策问题中的信息价值,给出了方法合理性的证明,并结合实例演示了求解方法。
信息价值;决策树;决策分析;贝叶斯分析
1 信息的期望价值求解
1.1 信息价值的概念
在决策过程中,可以通过随机试验获得观察值x,去改进决策人设定的自然状态θ的先验概率π(θ),从而减少期望损失。但是由于随机试验或高或低,所以通常试验前要考虑试验的成本与价值。如果通过试验收集到的新信息所降低的损失还不足以支付试验费用,则试验不值得进行,反之,随机试验才算获得额外价值。这种在决策中进行随机实验带来的额外收益(也就是期望损失的减少)称为信息价值[1]。
1.2 完全信息的期望价值
所谓完全信息的期望价值是指在理想情况下,通过试验能够获得自然状态θ的完全信息,那么决策人就可以事先知道状体θ的确切值,进而根据这种状态来选择似的损失最小的行动。完全信息的期望价值就是这种获得自然状态完全信息的随机试验带来的期望损失减少量。
1.3 采样信息的期望价值
因为完全信息的情况几乎不能实现,那么也无法根据完全信息带来的价值来评估随机试验的效果。所以在一般决策过程中,我们只考虑采样信息价值。采样信息价值是通过试验收集新信息来指导决策后,期望损失比采样之前的期望损失的减少量。
1.4 传统采样信息的期望价值求法
传统的采样信息价值求解中,需要先计算采样之前的贝叶斯风险的期望值:。具体而言,就是在不进行随机试验的情况下,仅仅依据未来状态的先验概率分布,求解每种行动带来的期望损失Eπ[l(θ,a)]。之后在所有行动的后果的期望损失中取最小值,此时的ai作为行动方案,此时的期望损失作为不进行随机试验的期望损失。
1.5 基于决策树的采样信息的期望价值求法
但是传统方法求解,需要根据不同的贝叶斯规则分别计算期望损失,当实验结果较多或者行动选择较多的情况下,规则十分多,计算量大,步骤繁琐重复,带来众多麻烦。所以需要寻求快速准确的方法来计算信息价值。
根据贝叶斯分析的第二扩展型得到,在进行随机试验之后,最佳决策规则应该是等价于对应每一种x∈X,选择一个a,使得积分r’’=∑l(θ,δ(x))π(θ|x)达到为极小,就能得叶斯叶斯规则。所对应的a也就是最佳行动的决策方案,得到的Eπ,所以我们在求解时候只需要针对每一个x∈X,选择最佳行动ai,得到的规则就是最佳规则δi(x)——贝叶斯规则。
这种最佳规则的决策,与决策树的思想一致,即在excel的宏treeplan中,选择决策树终端为每个分支行动或状态对应的损失值(默认终端为求和,此处可以修改为相应损失函数),每个决策节点选择较小的分支作为行动。这样自动选择了贝叶斯规则中对每种实验结果得到的最佳行动。
这样在每个决策分支都存在此分支下的期望损失,为了用决策树计算信息价值,就不要将进行试验预测的费用写入决策树中成本的部分,而是单纯计算进行预测和不预测的两种情况下的各分支期望损失。这样构造的决策树在是否进行预测的分支上得出的期望值就是进行预测和不进行预测两种情况下的期望损失。最后在excel表格中任意空白表格计算进行预测和不进行预测的期望损失之差,就是此预测信息的价值。将得到的信息价值与试验成本做比较,可以判断是否进行试验预测。
2 基于决策树的信息价值求法实例
2.1 实例
举个案例说明:某农民拟在两种作物中选择一种。若旱年θ1占60%,正常年景θ2占40%;种植耐旱作物a1以及不种植耐旱作物a2的后果矩阵如表1所示(单位:万元)。
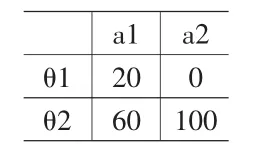
表1
设该农民的效用函数为μ(y)=1.156(1-e-0.02y(单位:万元),并且如果存在天气预报,并且天气预报的准确性为0.8,请问农民应该采取什么样的行动,天气预报的信息价值是多少?
2.2 后验概率求解
因为天气预报的准确性为0.8,设x1为预报为旱年,x2为预报为正常年景,P(θ1)=0.6,P(θ2)=0.4。所以P(x1|θ1)= 0.8,P(x2|θ1)=0.2,P(x1|θ2)=0.2,P(x2|θ2)=0.8
得到预报旱灾概率P(x1)=P(x1|θ1)P(θ1)+P(x1|θ2)P(θ2)=0.48+0.08=0.56
预报正常年景概率P(x2)=P(x2|θ1)P(θ1)+P(x2|θ2)P(θ2)=0.12+0.32=0.44
得到各种可能的后验概率为:
预报旱灾,发生旱灾概率为π(θ1|x1)=P(x1|θ1)P(θ1)/P(x1)=0.48/0.56=0.857143
预报旱灾,正常年景概率为π(θ2|x1)=P(x1|θ2)P(θ2)/P(x1)=0.08/0.56=0.142857
预报正常年景,发生旱灾的概率π(θ1|x2)=P(x2|θ1)P(θ1)/ P(x2)=0.12/0.44=0.2727273
预报正常年景,正常年景的概率π(θ2|x2)=P(x2|θ2)P(θ2)/ P(x2)=0.32/0.44=0.7272727
令损失函数l(y)=-u(y)
2.3 正规贝叶斯分析的方法求解
进行正规性贝叶斯分析,对以下四种策略进行比较:
策略1:收听天气预报,若预报旱灾则种植耐旱作物,预报正常则种植非耐旱作物。
期望损失为r(π,δ1)=πx1*(π(θ1|x1)*l(a1|θ1)+π(θ2|x1)*l (a1|θ2))+πx2(π(θ1|x2)*l(a2|θ1)+π(θ2|x2)*l(a2|θ2)=0.86*(-0.38) +0.14*(-0.81)+0.27*0+.73*(-1)=-0.57
策略2:收听天气预报,若预报旱灾则种植不耐旱作物,预报正常则种植耐旱作物期望损失为r(π,δ2)=πx1*(π(θ1|x1) *l(a2|θ1)+π(θ2|x1)*l(a2|θ2))+πx2(π(θ1|x2)*l(a1|θ1)+π(θ2|x2)*l (a1|θ2)=0.56*(0.86*0+0.14*(-1))+0.44*(0.27*(-0.38)+ 0.73*(-0.81))=22-0.38
策略3:忽略天气预报,不论预报是否旱灾,都种植耐旱作物期望损失为r(π,δ3)=Pθ1*l(a1|θ1)+Pθ2*l(a1|θ2) =-0.55
策略4:忽略天气预报,不论预报是否旱灾,都种植不耐旱作物期望损失为r(π,δ4)=Pθ1*l(a2|θ1)+Pθ2*l(a2| θ2)=-0.40
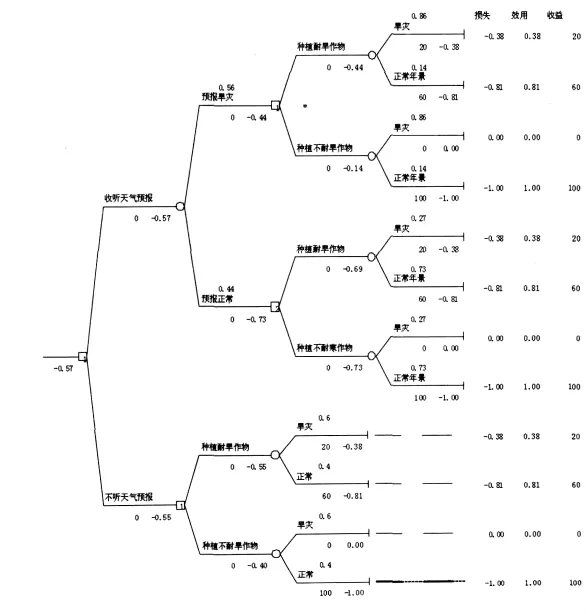
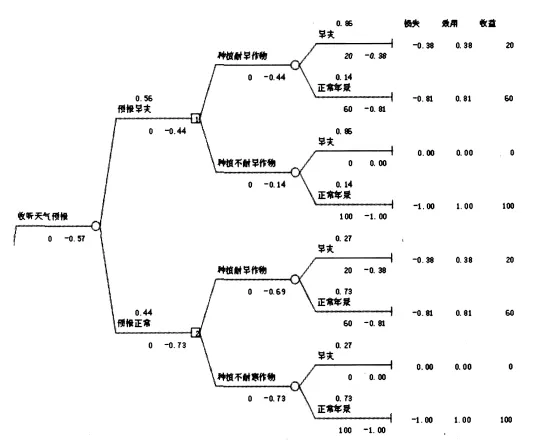
四种策略比较得到r(π,δ1) 所以行动方案一为最佳规则,即天气预报预报旱灾则种植耐旱作物,预报正常则种不耐旱作物。信息价值 此方法在此例中需要计算四种策略中的期望损失,步骤重复,较为麻烦,如果行动选择更大,随机试验结果更多,策略数量过多不易穷举,计算量也将十分大。 不考虑天气预报的成本前提下,不在决策树中进行预测的成本,并且在决策树分支末端输入损失函数l(y)=-μ(y)=-1.156(1-e-0.02y),并在末端单元格的右侧输入效用函数和收益。构造决策树如下,用于比较农民是否收听天气预报和采取不同策略的后果。 按照上文所述的决策树方法,决策点1的两分支的期望损失就分别为收听天气预报和不收听天气预报的期望损失,二者之差就是天气预报的信息价值。 这种方法的原理很容易理解,一句话概括就是决策树的决策选择方式恰好符合决策问题的贝叶斯规则。直观上来看,决策树在每个决策节点都选择在不同未来状态下的期望损失最小值,这个思路正与贝叶斯分析第二种扩展型完全符合。决策树根据试验的每种结果,都相应采取是的期望损失最小的行动,那么这种决策规则就是最佳决策规则,此时的贝叶斯风险为极小。也等价于取达到为极小,就能得到贝叶斯规则正规性中采取不同决策规则中得到的期望损失极小值而上图决策树中决策节点1的的上面分支,求出了进行预报后的贝叶斯风险最小值;下面一支中,恰好求出了不进行试验的贝叶斯损失最小值。所以二者的差值就是信息价值。 正如前文所述,决策树方法之所以可以十分方便地求解信息价值,是因为决策树的判断规则与贝叶斯分析的第二种扩展型一致。那么我们就用应用第二种扩展型求解此实例,并与决策树方法比较。 A:当取x1(预报旱灾) 采取行动a1:r1’’=l(θ1,a1)π(θ1|x1)+l(θ2,a1)π(θ2|x1) =(-0.38)*0.86+(-0.81)*0.14=-0.4402 采取行动a2:r2’’=l(θ1,a2)π(θ1|x1)+l(θ2,a2)π(θ2|x1) =(0)*0.86+(-1)*0.14=-0.14 采取行动a1 B:当取x2(预报正常) 采取行动a1:r3’’=1(θ1,a1)π(θ1|x2)+l(θ2,a1)π(θ2|x2)=-0.69 采取行动a2:r4’’=l(θ1,a2)π(θ1|x2)+l(θ2,a2)π(θ2|x2)=-0.73 所以采取行动a2 所以贝叶斯规则δπ:a1=δπ(x1),a2=δπ(x2) 这里面不同决策的期望损失恰好与下图决策树分支的四种情况完全一致。可见决策树方法与贝叶斯分析第二种扩展型的思路的一致。 传统信息价值的求法公式复杂、计算费时,而决策树是求解效用问题的实用方法,因此用决策树方法求解信息价值,在excel中自动计算,具有应用意义。在计算中,只需确定要求解哪项信息的价值,并求出各种情况的后验概率,进而构造决策树,就可十分方便地计算出决策问题中的信息价值。所有计算都可由excel自动完成,没有重复步骤。在处理行动选择很多、实验结果很多的实际问题中,仍可以很好的应用。 [1]岳超源.决策理论与方法[M].北京:科学出版社,2006. [2]王宏.基于属性约简的决策树构建[J].统计与决策,2006,(7). [3]孟飞翔,帅立国,姜昌金.决策树在客户价值分析中的应用[J].计算机技术与发展,2007,(7). [4]Quinlan J R.Induction of Decision Trees[J].Machine Learning,1986, (4). (责任编辑/亦民) F224 A 1002-6487(2010)22-0054-03
2.4 决策树方法求解信息价值
3 关于决策树方法的思考
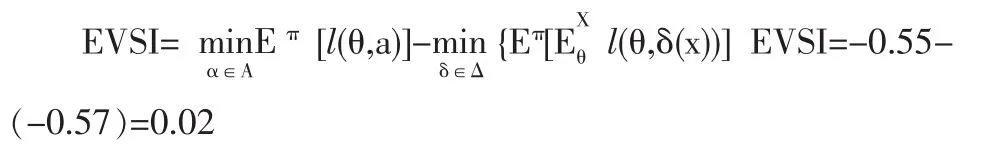
4 结论
