唐山市人口数值预测
2010-10-17武志勇霍晓姝刘家顺
武志勇,霍晓姝,刘家顺
(河北理工大学经济管理学院,河北唐山 063009)
唐山市人口数值预测
武志勇,霍晓姝,刘家顺
(河北理工大学经济管理学院,河北唐山 063009)
人口预测;马尔萨斯人口模型;逻辑斯蒂人口模型
分析了 1978年以来唐山市人口发展的现状,选择唐山市 1978—2005年的总人口统计数据来建立马尔萨斯人口模型和Logistic人口模型,并运用 2006—2007年的总人口数据来验证模型,对唐山市未来 8年的总人口数进行了预测,以期对唐山市统筹人口发展提供借鉴。
人口问题已成为我国面临的重要问题之一。唐山市正处在经济快速增长的过程中,作为一个重工业城市,同时面临人口、资源、环境与就业等问题的压力。适度的人口规模是经济、社会、资源和环境保护协调发展的强有力保证。认识人口数量的变化规律,建立人口模型,作出较准确的预报,是有效控制人口增长的前提。
18世纪末,英国人口学家马尔萨斯对百余年的人口统计资料进行了研究,于 1798年提出人口指数增长模型。他的基本假设是:单位时间内人口的增长量与当时的人口总数成正比。但从长期来看,任何地区的人口都不可能无限增长,由于受到自然资源、环境条件等因素的影响,而当人口增加到一定数量以后,这个增长率就要随着人口的增加而减少。为此,荷兰生物数学家Verhulst在 19世纪中叶提出了阻滞增长模型,即逻辑斯蒂 (Logistic)模型。
一 唐山市总人口及其增长率的变化趋势分析
从图 1可以看出,唐山市总人口从 1978年的 558.47万人增加到 2007年的 724.66万人,30年时间增加了166.19万人,平均年增长率为 7.17‰。
唐山市 1978年至今总人口数的变化趋势主要表现为:总人口数逐年增长,年增长率的总的趋势是高—低—高—更低,1978—1982年以及 1987—1990年进入高增长期,平均增长率达到 12.27‰;1983—1986年比较低,平均为7.65‰;1991年之后人口增长率处于更低水平,平均为4.35‰,且总体趋势平稳,这一定程度上反映了唐山市计划生育近些年取得了一定的成效。与此同时,我们还应看到:尽管近年来,唐山市人口增长速度较慢,但每年出生人口的绝对数仍然很大,未来相当一段时间内将是人口数量庞大和人口持续增长并存。

图1 唐山市历年人口数及增长率数据来源:2007年唐山市统计年鉴
二 模型预测
1978年之后我国计划生育进入蓬勃发展时期,本文选择唐山市 1978—2005年的人口统计数据来建立马尔萨斯人口模型、阻滞增长模型,运用 2006—2007年的总人口数据来验证模型,以此来预测唐山市未来 8年的总人口数。
1 马尔萨斯人口模型
英国人口学家马尔萨斯根据百余年的人口统计资料,提出了著名的基于指数增长的人口模型。该模型假设人口的增长率是常数。
我们可以近似地认为人口数 P(t)是时间变量 t的连续可微函数。以 r(t,p)表示人口出生率与死亡率之差,记为人口的净增长率 (或叫做自然增长率),则有
假定净增长率 r(t,p)为一常数,仍记为 r。并且在时刻 t0人口数为 p0,则得初值问题

解得它说明人口是依指数函数的规律增长的。这就是著名的马尔萨斯人口论的数学模型。
唐山市 1978—2005年的年平均人口增长率为 7.28‰,但是考虑到近十几年增长率趋于平稳,所以这里取 1991—2005年增长率为取值空间,认为 1991—2005年唐山市人口年均增长率保持现有水平 4.19‰不变,以 2005年为基准年,推断出 2006、2007年人口数,以 2007年实际根据统计数据为基准年,运用马尔萨斯人口模型,可以得到 2008~2015年唐山市总人口的预测数据,具体数据见表 1。


表 1 唐山市 2006—2015年人口预测 (单位:万人)
由表中数据可以看到,“十一五”最后一年 2010年,总人口数达到 733.83万,到“十二五”最后一年 2015年唐山市人口达到 749.36万人。
2 逻辑斯蒂人口增长模型
由方程 (3)当 r>0时人口数将无限增加,这显然是不符合实际情况的。由于受到自然资源,食物、医疗卫生、环境等条件的限制,人口数的增加是不可能无限制的。因此,人们在马尔萨斯律上又加了一个 “竞争项”—bp (t)2,于是有

其中 a>0,b>0都是常数,且数值很小。非线性方程 (4)称为生物群体增长的逻辑率,a,b称为生命系数。(4)是个变量可分离的方程,加上初始条件 p(t0) =p0,

显然有

模型 (5)称为 Logistic模型。利用导数做出函数 (5)的图像,如图 2所示它是一条“S”形曲线,可以看到:当总人口数未达到 a/2b时是加速增长时期,过了 a/2b后是减速增长时期,但增长率为正,随时间的增加而减少,t→+∞,p′→0。
为了计算模型 (5)中的 a,b选择 t0,t1,t2三年的数据 p0=p(t0),p1=p(t1),p2=p(t2),其中 t1-t0=t2-t1=T,代入模型 (5)有

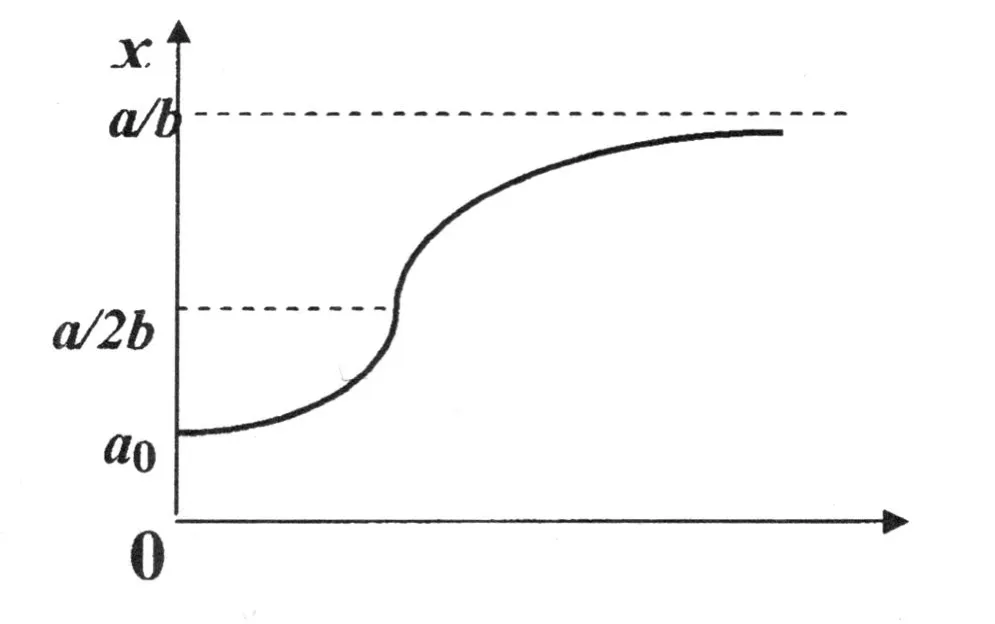
图 2 Logistic模型
解得

我们选择 1991年、1997年、2003年间距相等的三个年份 p(1991) = 6 627 690,p(1997) =6 883 354,p(2003) =7 062 834,计算得 a=0.037 2,b=0.4×10-8。
将 a=0.0372,b=0.4×10-8代入 (5)得到唐山市人口增长的计算公式:

从上可知,唐山市的人口极限约为 a/b=930(万)。并且由该公式预测出唐山市2006年到2014年的总人口数如表2:

表 2 唐山市 2006年到 2014年的总人口数预测表 (单位:万人)
三模型的验证及未来人口预测
将 2005年、2006年的人口预测值与实际统计值之间进行比较,由表 3可以看出,两种模型的相对误差都较小,且一正一负,故本文采用两种预测的平均值作为 2008—2014年总人口数的最终预测结果。

表 3 2005、2006年的人口预测值与实际统计值 (单位:万人)的误差
对应计算数据其误差情况如表 4,相对误差相对更小,数据也更加精确。

表 4 2005、2006年的平均人口预测值与实际统计值(单位:万人)的误差
通过加权平均可以得到未来 8年中人口预测值,如图 3所示,可以看到,唐山市人口规模呈现较稳定的增长趋势,“十一五”最后一年 2010年,人口规模估计会达到 737.89万,而到 “十二五”最后一年 2015年人口规模将达到758.84万。
人口增长同时受诸多因素的影响,所以,任何一种模型都不可能精确无误地预测,但本文认为其结果还是具有一定的参考价值。

图3 唐山市人口数值预测
[1] 邵晓锋,张克新 .黄冈市人口增长模型的研究 [J].数学的实践与认识,2008,7(13).
[2] 李绍成 .我国人口增长的数学模型探讨 [J].绵阳农专学报,1994,11(1).
[3] 何万生,等 .数学模型与建模 [M].甘肃教育出版社, 2001.
[4] 唐山统计年鉴 [M].中国统计出版社,2008.
[5] 刘华中 .Logistic模型在人口预测中的应用 [J].江苏石油化工学院学报,1998,10(1).
[6] 贾晓峰,等 .微积分与数学模型 [M].高等教育出版社, 1999.
Key words:population forecast;malthus population model;logistic population model
Abstract:The article analyzes present situation of Tangshan population development in 1978,chooses the total population statistical data of Tangshan in 1978~2005 year to establish theMalthuspopulation model and the Logistic population model,and tests the model by using 2006~2007 year total population data,it also carries on the forecast on next eight years in Tangshan,which would provide reference to overall plan population development in Tangshan.
Research on the Forecast of Population Value of Tangshan
WU Zhi-yong,HUO Xiao-shu,L IU Jia-shun
(College of Economics andManagement,Hebei Polytechnic University,Tangshan Hebei 063009,China)
C 923
A
1673-2804(2010)05-0019-03
2009-12-17
